
- •Конспект лекций
- •§2. Основные операции над матрицами и их свойства
- •§3. Линейная зависимость и независимость вектор-столбцов
- •§4. Определители второго и третьего порядков
- •§5. Определитель порядка n
- •§6. Свойства определителей
- •§7. Обратная матрица
- •§1. Основные определения
- •§2. Формулы Крамера для решения системы линейных уравнений
- •§3. Решение системы линейных уравнений с помощью обратной матрицы
- •§4. Решение системы линейных уравнений методом Гаусса
- •§5. Теорема Кронекера-Капелли
- •I Понятие ранга матрицы.
- •II Критерий совместности системы линейных уравнений
- •Раздел II Аналитическая геометрия.
- •§1. Действительные числа. Числовая ось
- •§2. Системы координат
- •I Система координат на прямой
- •II Декартова прямоугольная система координат на плоскости
- •III дпск в пространстве
- •IV Полярная система координат
- •§3. Векторы: основные определения
- •§4. Линейные операции над векторами
- •I Сложение векторов
- •II Умножение вектора на число
- •III Вычитание векторов
- •IV Основные свойства линейных операций
- •§5. Проекции вектора на оси. Направляющие косинусы
- •§6. Разложение вектора
- •I Частный случай
- •II Общий случай
- •§7. Скалярное произведение векторов
- •I Определение
- •II Механический смысл
- •II Свойства скалярного произведения
- •IV Выражение скалярного произведения через проекции
- •§8. Векторное произведение векторов
- •I Определение
- •II Механический смысл
- •III Свойства векторного произведения
- •IV Выражение векторного произведения через проекции
- •§9. Смешанное произведение трех векторов
- •I Правые и левые тройки векторов
- •II Определение смешанного произведения и его смысл
- •III Выражение смешанного произведения через проекции
- •IV Условие компланарности векторов
- •§1. Уравнение линии на плоскости
- •I Две задачи аналитической геометрии.
- •II Параметрическое задание линии
- •III о пересечении двух линий
- •IV Уравнение линии в различных системах координат
- •§2. Общее уравнение прямой на плоскости
- •§3. Уравнения прямой с угловым коэффициентом
- •§4. Взаимное расположение двух прямых
- •§5. Расстояние от точки до прямой на плоскости
- •§6. Другие формы уравнения прямой на плоскости
- •I Каноническое уравнение
- •II Уравнение прямой “в отрезках”.
- •III Параметрические уравнения прямой
- •IV Полярное уравнение прямой
- •§1. Уравнение поверхности и уравнения линии
- •I Поверхность
- •II Линия в пространстве
- •§2. Общее уравнение плоскости
- •§3. Неполные уравнения плоскости
- •§4. Взаимное расположение двух плоскостей
- •§5. Расстояние от точки до плоскости
- •§6. Другие виды уравнения плоскости
- •I Уравнение плоскости, проходящей через три точки
- •II Уравнение плоскости “в отрезках”
- •§7. Прямая в пространстве
- •I Общие уравнения прямой
- •II Канонические уравнения прямой
- •III Параметрические уравнения прямой
- •§8. Расстояние от точки до прямой в пространстве
- •§9. Взаимное расположение двух прямых в пространтве
- •§10. Взаимное расположение плоскости и прямой в пространстве
- •§1. Общее уравнение
- •§2. Окружность
- •§3. Эллипс
- •I Каноническое уравнение эллипса
- •II Определяющее свойство эллипса
- •III Элементы эллипса
- •IV Нормальное уравнение эллипса.
- •V Параметрические уравнения эллипса (1):
- •§4. Гипербола
- •I Каноническое уравнение гиперболы
- •II Определяющее свойство гиперболы
- •III Элементы гиперболы
- •IV Нормальное уравнение гиперболы
- •§5. Парабола
- •I Каноническое уравнение параболы
- •II Определяющее свойство параболы
- •III Элементы параболы
- •IV Нормальное уравнение параболы
- •§6. Касательные к кривым 2го порядка
- •I Определения
- •II Уравнения касательных
- •III Некоторые свойства касательных
- •Вопросы к модульному контролю – 1.1
- •Образец билета мк-1.1
- •Учебное издание конспект лекций
- •6.050102 “Программная инженерия”)
§2. Основные операции над матрицами и их свойства
Прежде всего, договоримся считать две матрицы равными, если эти матрицы имеют одинаковые размеры и все их соответствующие элементы совпадают.
Перейдем к определению операций над матрицами.
1) Сложение матриц. Сумой двух матриц A=(aij) и B=(bij) одного и того же размера m×n называется матрица C=(cij) того же размера m×n , элементы которой равны
сij = aij + bij (i=1,2, … , m; j=1,2, … ,n). (1)
Для обозначения суммы матриц используется запись C=A+B.
2) Умножение матрицы на число. Произведением (m×n)-матрицы А на число λ называется (m×n)-матрица C=(cij), элементы которой равны
сij = λ aij (i=1,2, … , m; j=1,2, … ,n). (2)
Для обозначения произведения матрицы на число используется запись C= λ∙A.
Непосредственно из формул (1) и (2) ясно, что две введенные операции обладают свойствами:
а) А+В = В+А – коммутативность сложения ;
б) (А+В)+С = А+(В+С) – ассоциативность сложения;
в) (λμ)А=λ(μА) – ассоциативность умножения на число;
г) λ(А+В) = λА+λВ – дистрибутивность умножения относительно сложения.
Замечание 1. Разность матриц можно определить следующим образом:
А–В = А+(–1)В.
Кратко говоря, сложение, вычитание матриц и умножение матрицы на число производится поэлементно.
Пример:
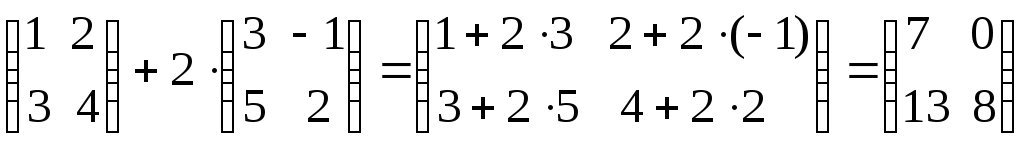 .
.
3) Умножение матриц. Произведением (m×n)-матрицы А=(аij) на (n×p)-матрицу B=(bij) называется (m×p)-матрица С=(сij), элементы которой вычисляются по формуле
cij=ai1b1j+ai2b2j+…+ainbnj ,
которую с использованием символа суммирования можно записать в виде
![]() (i=1,2,
… , m;
j=1,2,
… ,
p).
(i=1,2,
… , m;
j=1,2,
… ,
p).
Для обозначения произведения матрицы А на матрицу В используют запись С=А∙В.
Сразу заметим, что матрицу А можно умножить не на всякую матрицу В: необходимо, чтобы число столбцов матрицы А было равно числу строк матрицы В.
Формула (3) представляет правило нахождения элементов матрицы А∙В. Сформулируем это правило словесно: элемент cij , стоящий в i-й строке и j-ом столбце матрицы А∙В, равен сумме попарных произведений соответствующих элементов i-й строки матрицы А и j-го столбца матрицы В.
Приведем пример умножения квадратных матриц второго порядка:
 .
.
Умножение матриц обладает свойствами:
а) (АВ)С = А(ВС) – ассоциативность;
б) (А+В)С = АС+ВС или А(В+С) = АВ+АС – дистрибутивность умножения относительно сложения.
Вопрос о коммутативности умножения имеет смысл ставить лишь для квадратных матриц одинакового порядка, ибо только для таких матриц А и В оба произведения АВ и ВА определенны и являются матрицами одинаковых порядков. Элементарные примеры показывают, что умножение матриц, вообще говоря, некоммутативно. Например, если
![]() то
то
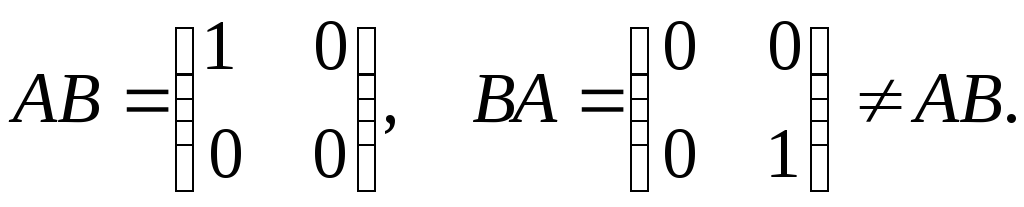
Пример.
Для матрицы
![]() найти все
матрицы
В
такие,
что
найти все
матрицы
В
такие,
что
АВ = ВА.
Решение.
Введем обозначение
![]() Тогда
Тогда

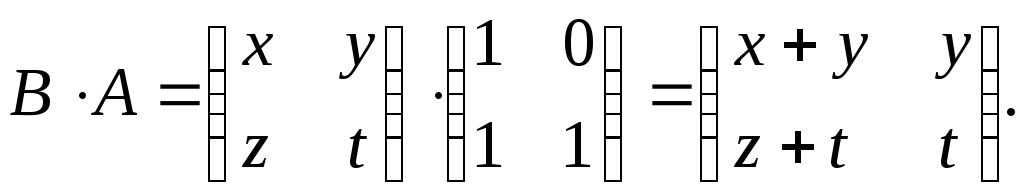
Равенство АВ =ВА равносильно системе уравнений
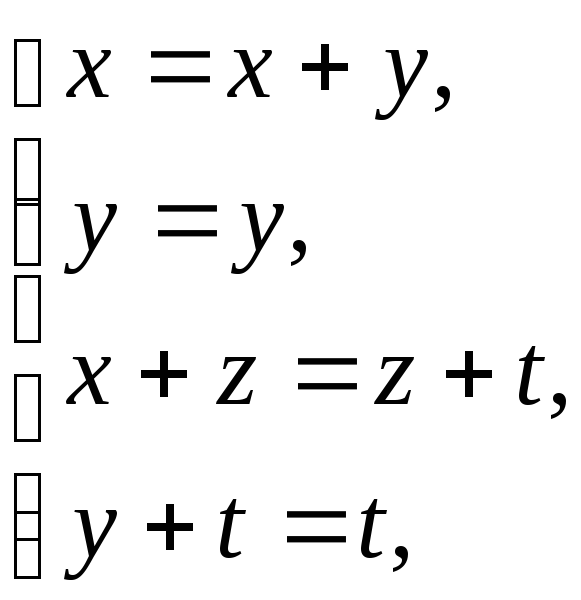
которая,
в свою очередь, равносильна системе
![]()
Итак,
искомая матрица имеет вид
![]() гдеx
и z
– произвольные
числа.
Её можно
записать и так:
В
= zA+(x–z)E.
гдеx
и z
– произвольные
числа.
Её можно
записать и так:
В
= zA+(x–z)E.
Замечание. Единичная и нулевая матрицы n-го порядка перестановочны с любой квадратной матрицы того же порядка, причем АЕ = =ЕА = А, А∙0 = 0∙А = 0.
Используя операцию
умножения, дадим наиболее краткую –
матричную – форму записи системы
линейных уравнений (1.1). Введем обозначения:
А=(аij)
– (m×n)-матрица
коэффициентов системы уравнений;
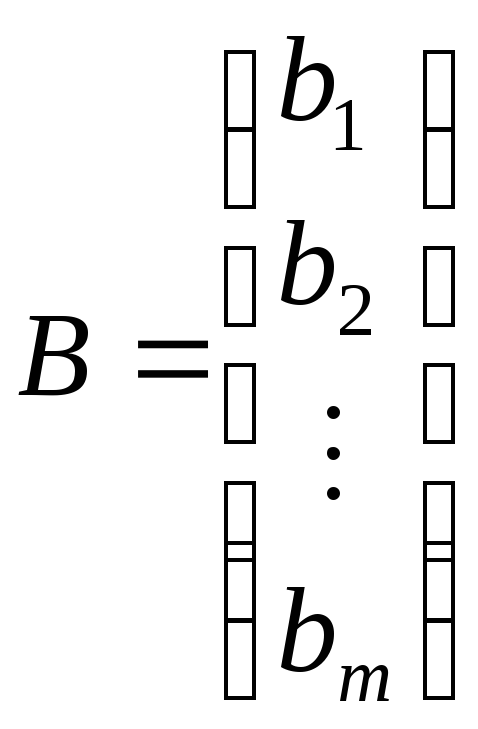 –m-мерный
столбец свободных членов и
–m-мерный
столбец свободных членов и
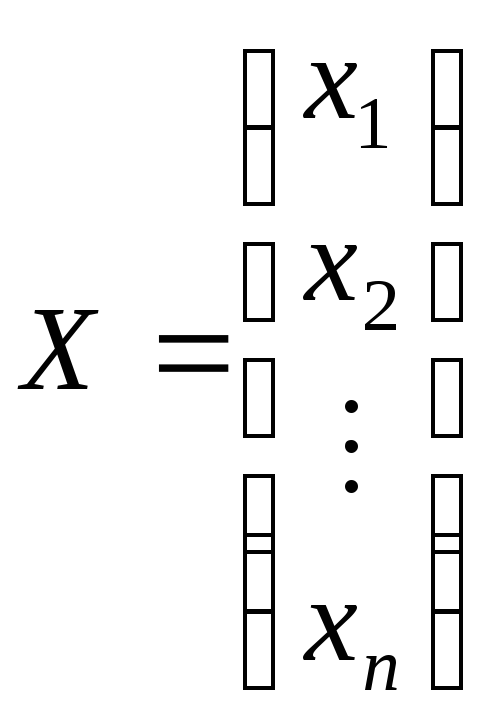 –n-мерный
столбец неизвестных. Согласно определению
произведение А∙X
представляет собой m-мерный
столбец. Его элемент, стоящий в i-й
строке, имеет вид
–n-мерный
столбец неизвестных. Согласно определению
произведение А∙X
представляет собой m-мерный
столбец. Его элемент, стоящий в i-й
строке, имеет вид
ai1x1+ai2x2+…+ainxn .
Но эта сумма есть не что иное, как левая часть i-го уравнения системы (1.1) и по условию она равна bi , т.е. элементу, стоящему в i-й строке столбца В. Отсюда получаем: А∙X = В. Это и есть матричная запись системы линей-
ных уравнений. Здесь: А – матрица коэффициентов системы, В – столбец свободных членов, X – столбец неизвестных.
4) Транспонирование матрицы. Транспонированием любой матрицы называется операция, в результате которой меняются местами строки и столбцы с сохранением порядка их следования. В результате транспонирования (m×n)-матрицы А получается (m×n)-матрица, обозначаемая символом А´ и называемая транспонированной по отношению к матрице А.
Пример. Для А = (а1 а2 а3) найти А∙А´ и А´∙А.
Решение. Транспонированная строка – это столбец. Поэтому:
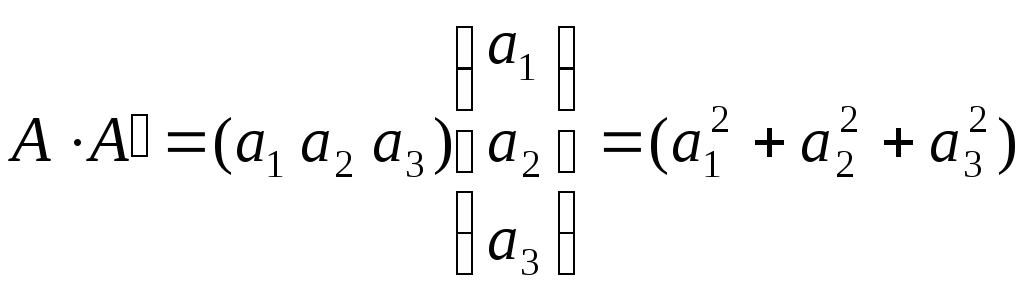 –квадратная
матрица 1го
порядка.
–квадратная
матрица 1го
порядка.
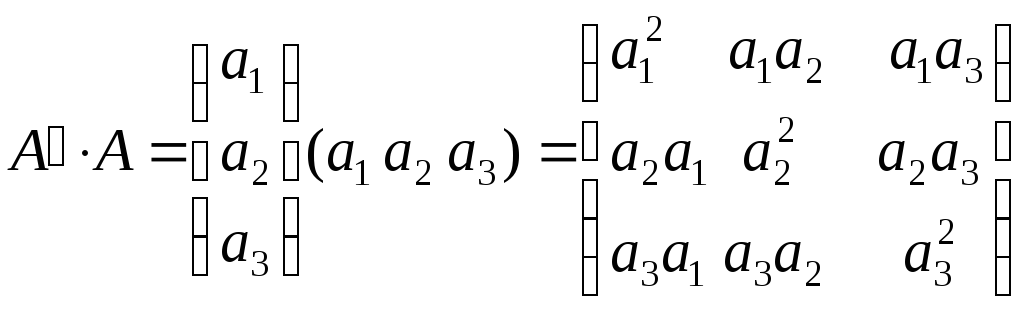 –квадратная матрица
3го
–квадратная матрица
3го
порядка.
