§6. Разложение вектора

I Частный случай

Пусть в пространстве дана ДПСК. Обозначим через – единичные векторы осейOx ,Oy и Oz соответственно ( они лежат на осях и направлены в положительные стороны).

Теорема 1. Всякий вектор можно представить (единственным образом) в виде линейной комбинации векторов:

. (1)

Схема доказательства

Пусть аА₁ и А₂ – проекции точки А на оси координат. Тогда (правило параллелограмма).

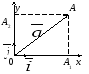
значит где. Аналогичногде.

Замечание 1. Представление вектора в виде (1) называют разло-48жениемпо базису. Слагаемые в правой части (1) называют ком- понентами вектора.

Замечание 2. Радиус-вектором точки М называют вектор , часто обозначаемыйили. Его проекции совпадают с координатами точкиМ: если M(x; y; z), то Полезная формула:

II Общий случай

Векторы называются линейно независимыми, если ни один из них не является линейной комбинацией других. Для двух векторов незави- симость равносильна неколлинеарности, а для трех – некомпланарности.

Говорят, что линейно независимые векторы образуют базис, если любой другой вектор является их линейной комбинацией.

Теорема 2. Любая тройка некомпланарных векторов образует базис в пространстве. Любая пара неколлинеарных векторов образует базис в плос- кости, содержащей эту пару векторов.

Другими словами, если – некомпланарные векторы, то для любого векторасуществуют (и притом единственные) числатакие, что

. (2)

Поиск коэффициентов линейной комбинации (2) сводится к решению системы линейных уравнений, матрица коэффициентов которой составлена из проекций векторов ,,(по столбцам), а свободные члены – это

проекции вектора .

Замечание к §3-6.

Студент должен уметь:

– выполнять действия с векторами в геометрической и координатной формах;

– находить проекции, длину, направляющие косинусы, орт вектора;

– разлагать вектор по базису;

– проверять коллинеарность и компланарность векторов.

ЛЕКЦИЯ 5

§7. Скалярное произведение векторов

I Определение

Скалярным произведением двух векторов иназывают число, обозначаемое символом, и вычисляемое по формуле

(1)

где φ – угол между векторами .

Вспоминая формулу для проекции одного вектора на другой, можно выразить скалярное произведение векторов идругими формулами:

(2)

II Механический смысл

Если вектор изображает силу, точка приложения которой перемещается из начала векторав его конец, то работа этой силы есть не

что иное, как .

II Свойства скалярного произведения

1. (коммутативность).

2. (ассоциативность относительно умножения на

число).

3. (дистрибутивность относительно сложения).

Замечание 1. Указанные свойства дают право при скалярном перемножении векторных многочленов выполнять действия почленно, не заботясь о порядке сомножителей. Например,

Замечание 2. Скалярного произведения трех векторов не существует.

4. Скалярное произведение называется скалярным квадратом вектораи обозначается символом. Скалярный квадрат вектора, равен квадрату его длинны:

.

Это свойство можно использовать для нахождения длин векторов. Например, найти длину вектора , гдеИмеем:

откуда .

5. Если , то(т.к.), но важно и обратное утверждение: если , то векторы взаимно перпендикулярны. Действительно, равенствовозможно, если: 1), или 2), или 3). В первом случае сразу получаем. Второй (третий) случай означает, что вектор() есть нулевой вектор, направление которого можно считать каким угодно, в частности перпендикулярным .

Сказанное выше можно сформулировать как условие перпендикулярности векторов:

векторы перпендикулярны тогда и только тогда, когда их скалярное произведение равно 0.