IV Выражение скалярного произведения через проекции

Пусть известны проекции векторов на оси некоторой ДПСК: Запишем разложения этих векторов по базису:

Базисные векторы – единичные, значит, их скалярные квадраты равны 1; они взаимно перпендикулярные значит . Перемножая разложения почленно, получим

. (3)

Это и есть формула, выражающая скалярное произведение векторов через их проекции на оси ДПСК.

Из формулы (3) можно получить ряд важных следствий.

1. Длина вектора вычисляется по формуле

.

2. Угол φ между векторами 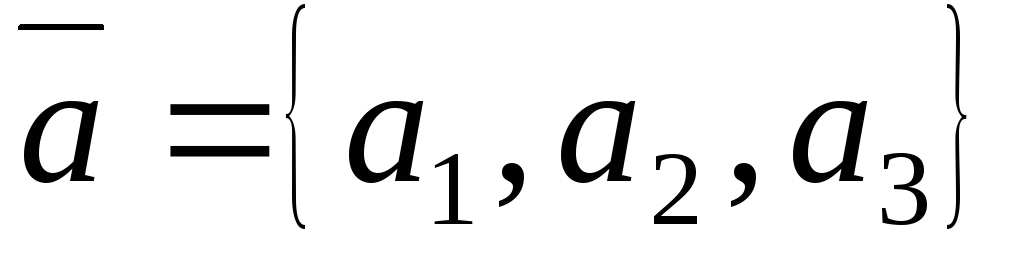иопределяется равенством

3. Необходимым и достаточным условием перпендикулярности векторов 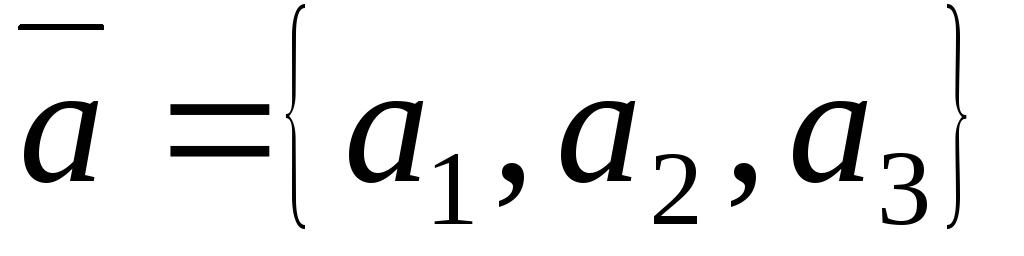и 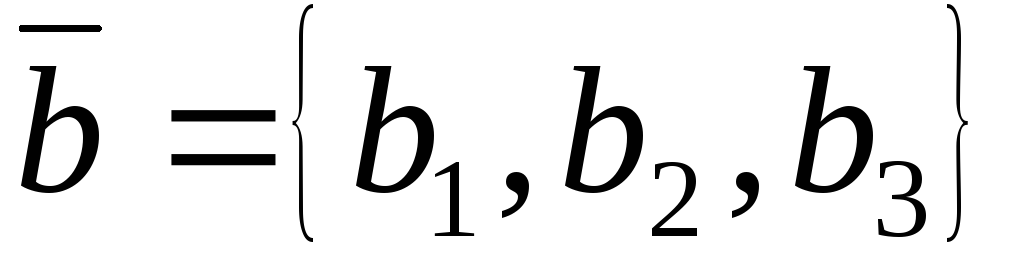является равенство

.

4. Если ось и составляет с осями координат углы , то проекция векторана эту ось определяется равенством

. (4)

Для доказательства (4) рассмотрим единичный вектор одинаково направленный с осьюи. Тогда: 1) ; 2)Но из определенияследует

.

Остается в этой формуле положить и воспользоваться формулой (3)

и тем, что

5. Если , то.

§8. Векторное произведение векторов

I Определение

Векторным произведением вектора на векторназывается вектор, который обозначается символоми определяется условиями:

1) (φ – угол между и);

2) и;

3) тройка векторов () является правой тройкой, т.е. из концакратчайший поворот отккажется совершающимся против часовой стрелки.

II Механический смысл

Если вектор изображает силу, приложенную к какой-нибудь точкеМ, а вектор идет из некоторой точкиО в точку М, то вектор представляет собой момент силыотносительно точкиО.

III Свойства векторного произведения

1. (антикоммутативность).

2. (ассоциативность по отношению к

числовому множителю).

3. (дистрибутивность относительно

сложения).

Замечание 1. Указанные свойства дают право при векторном перемножении векторных многочленов выполнять действия почленно, обращая внимание на порядок сомножителей.

4. (условие коллинеарности векторов).

Замечание 2. Так как всегда , то в векторной алгебре понятие векторного квадрата не употребляется.

5. Если векторы иприведены к общему началу, то модуль их векторного произведения равен площади параллелограмма, построенного на векторахи.

Пример. На векторах ипостроен параллелограммР₁ а на диагоналях его построен еще один параллелограмм Р₂. Как связаны площади этих параллелограммов?

Решение. Диагонали Р₁ – это сумма и разность и:Тогда площадь параллелограммаР₂:

Итак, площадь параллелограмма Р₂ в два раза больше площади параллелограмма Р₁.

IV Выражение векторного произведения через проекции

Приведем таблицу векторного умножения базисных векторов , легко получаемую из рисунка

В столбце базисных векторов приведены первые множители векторного произведения, а в строке – вторые.

Пусть известны проекции векторов ив некоторой ДПСК:,. Разложим векторы по базису

и векторно перемножим эти “многочлены” почленно. Учитывая приведенную таблицу, получим:

В этой формуле нетрудно заметить формальное разложение некоторого определителя третьего порядка по элементам, например, первой строки. Итак, имеем

Пример. Найти площадь ΔАВС, где А(1;1;1), B(2;2;2) и C(4;3;5).

Решение. Найдем векторы и. Перемножим их векторно:

Модуль этого вектора – это площадь параллелограмма, построенного на и , а половина этого модуля – искомая площадь треугольника:

Вектор обладает важным свойством, которое понадобится нам в дальнейшем: этот вектор перпендикулярен векторамиили, другими словами, этот вектор перпендикулярен плоскостиΔАВС.