§7. Обратная матрица

Пусть А – квадратная матрица n-го порядка, а Е – единичная матрица того же порядка.

Матрица В называется обратной по отношению к матрице А, если АВ=ВА=Е.

Теорема. Всякая матрица с отличным от нуля определителем (т.н. невырожденная матрица) имеет обратную и притом единственную.

Доказательство. Вычислим алгебраические дополнения A_ij всех n² элементов матрицы А, составим из них новую матрицу и транспонируем её. Получим т.н. союзную матрицу:

.

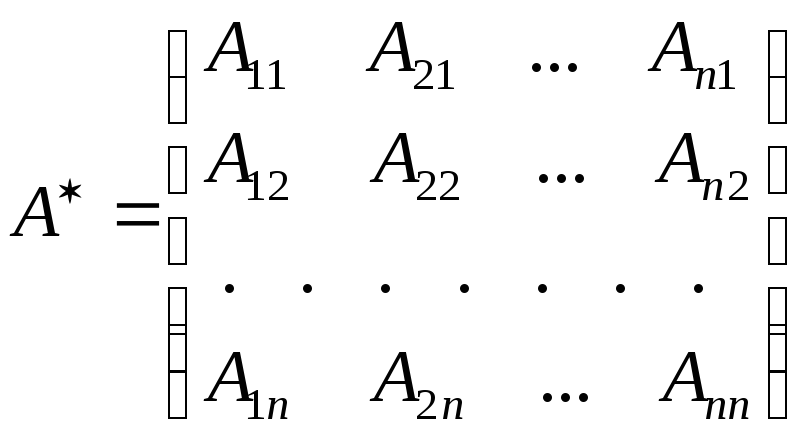Рассмотрим произведение матриц А∙А^*=(с_ij). Его элементы вычисляются по формуле . Если i=j, то эта сумма равна определителю ∆=det(A) (по определению), если же i≠j, то она равна 0 (по свойству 9). Итак, матрица А∙А^* имеет вид

=∆∙Е.

Но тогда . Аналогично можно показать, что иА*А=∆·Е и .Все это означает, что матрицаи есть обратная матрица по отношению к матрицеА.

Докажем единственность. Пусть существует еще одна матрица С (кроме построенной выше В) такая, что СА=АС=Е. Тогда: С=СЕ=С(АВ)=(СА)В=ЕВ=В, т.е. С совпадает с матрицей В. Теорема доказана.

Замечание. Матрицу обратную к матрице А, принято обозначать символом А^-1. В силу одного из свойств определителей.

Пример. Найти матрицу, обратную к данной

.

Решение. Убедимся, что матрица А невырожденная: Δ=а₁₁∙A₁₁=1∙(3∙5–3∙4)=3≠0. Находим алгебраические дополнения элементов матрицы А:

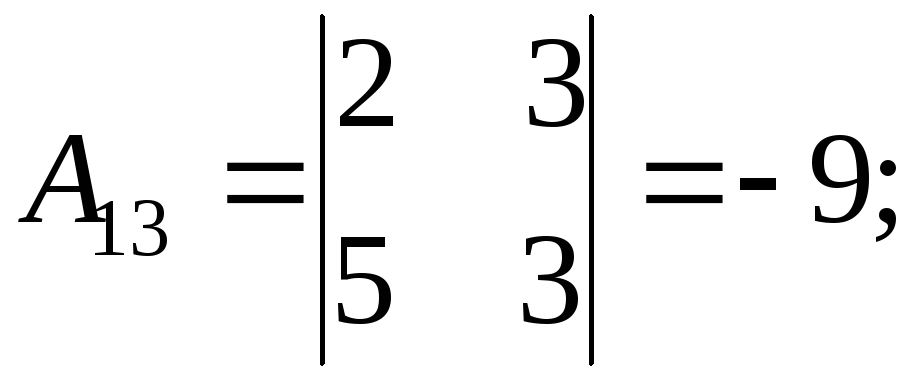
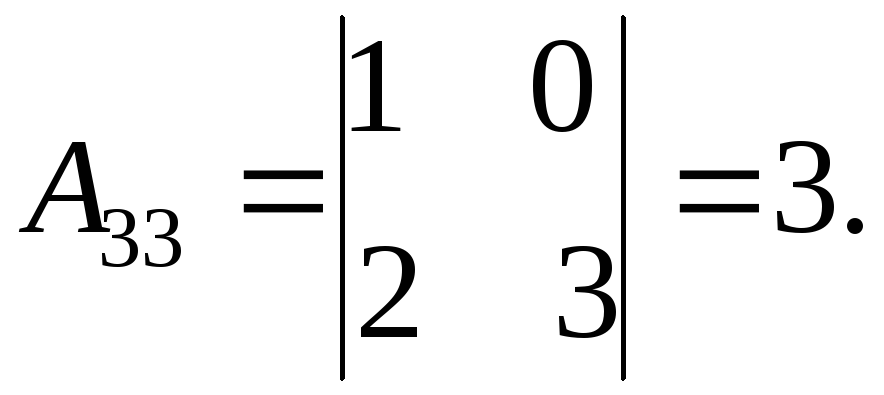
Составляем союзную матрицу

.

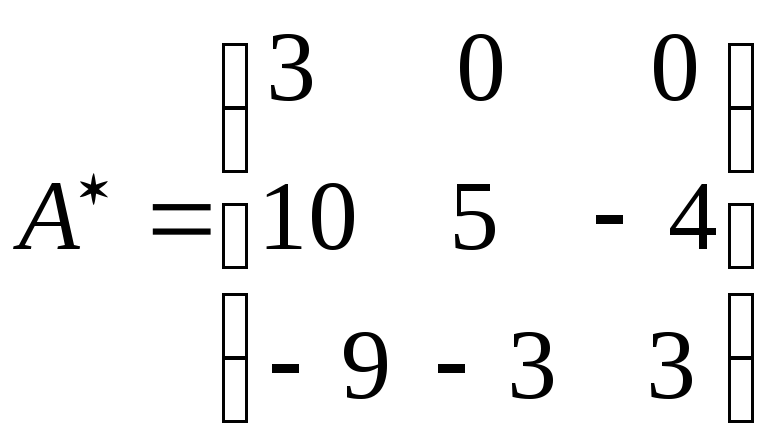Находим обратную матрицу

.

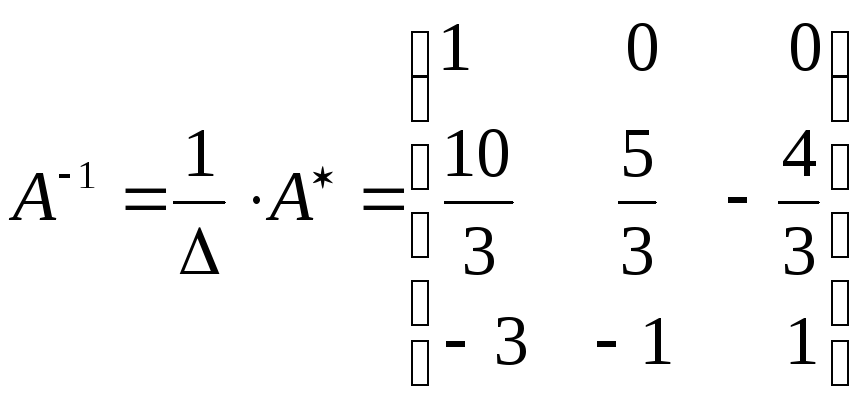ЛЕКЦИЯ 3

Тема Системы линейных уравнений

§1. Основные определения

В общем случае система m линейных уравнений с n неизвестными имеет следующий вид:

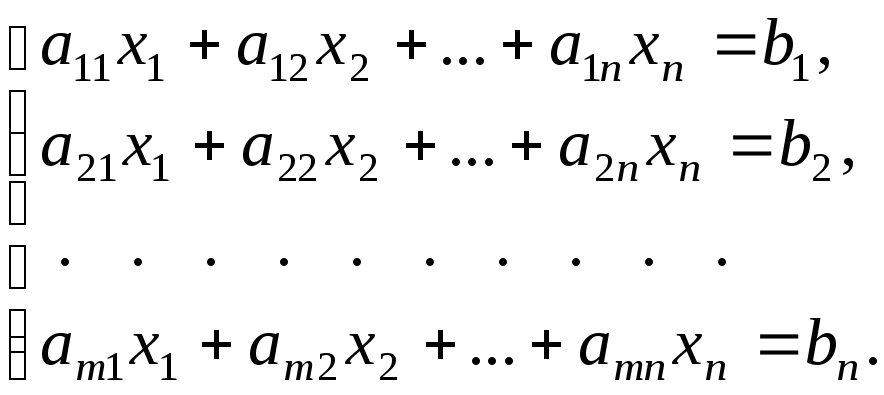(1)

При этом через x₁, x₂,…, x_n обозначены неизвестные, подлежащие определению, причем, их число n, не предполагается обязательно равным числу уравнений m. Величины a₁₁, a₁₂,…, a_mn , называемые коэффициентами системы, и величины b₁, b₂,…, b_n, называемые свободными членами, предполагаются известными.

Решением системы (1) называется такая совокупность n чисел c₁, c₂,…, c_n , что каждое из уравнений (1) обращаются в верное числовое равенство после замены в нем неизвестных x_i соответствующими числами c_i , i=1,2,…,n.

Система уравнений называется совместной, если она имеет, по крайней мере, одно решение, и несовместной, если у нее не существует ни одного решения.

Например, система

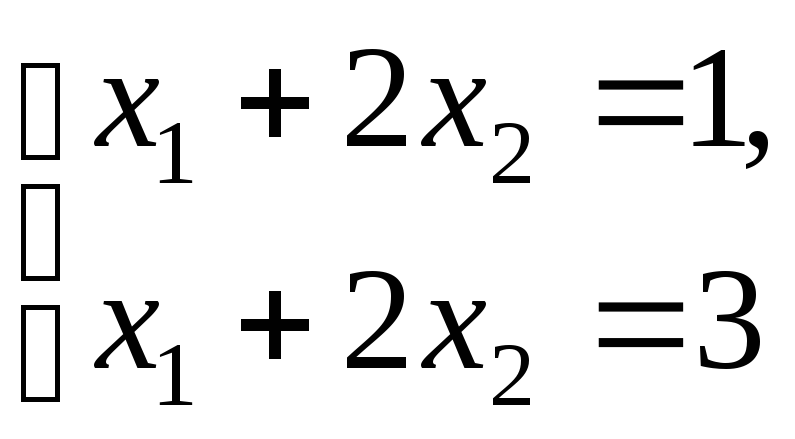
является несовместной, ибо в противном случае мы получили бы, что 1=3.

Решить систему уравнений означает найти все её решения или доказать, что она несовместна.

Два решения совместной системы с₁, с₂, …, с_n и d₁, d₂, …, d_n называют-

ся различными, если нарушается хотя бы одно из равенств с₁=d₁, c₂=d₂, …

…, c_n=d_n.

Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если у нее существуют, по крайней мере, два различных решения.

Система уравнений называется однородной, если свободные члены всех её уравнений равны нулю.

Очевидно, однородная система всегда совместна, ибо обладает решением x₁=0, x₂=0,…, x_n=0 (т.н. тривиальное решение).

Можно доказать, что, если система уравнений имеет два различных решения, то она имеет бесконечное множество решений.

Справедливость этого наглядно проявляется в случае системы двух уравнений с двумя неизвестными:

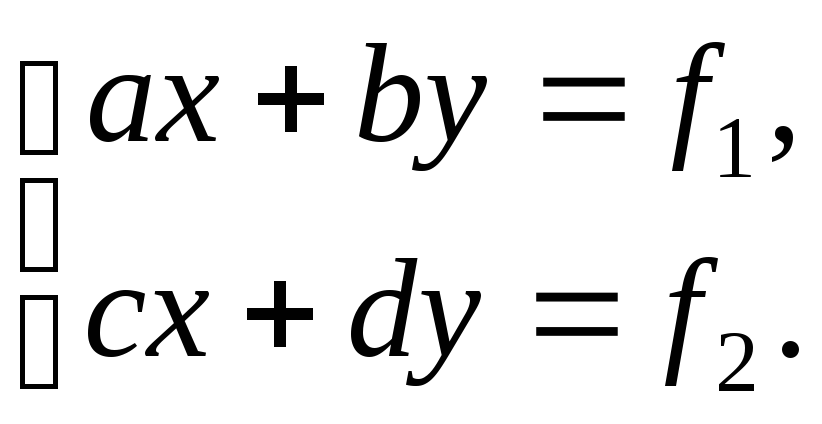(2)

Каждое уравнение системы (2) определяет на плоскости Oxy некоторую прямую. Решение системы (2) – это координаты общей точки двух прямых. Но у двух прямых может не существовать общих точек, быть только одна общая точка или бесконечно много общих точек ( если прямые совпадают ).

Две системы линейных уравнений называются эквивалентными (равносильными), если они или обе несовместимы, или же обе совместны и обладают одними и теми же решениями.