§4. Линейные операции над векторами

I Сложение векторов

Суммой векторов иназывают вектор, обозначаемый+, который идет из начала векторав конец вектора, при условии, чтоприложен к концу. (“правило треугольника”) .

Полезная форма записи

.

З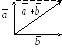амечание. Сумму векторов можно находить и по так называемому правилу параллелограмма: приведем векторы ик общему началу, построим на них параллелограмм, тогда+есть диагональ этого параллелограмма, идущая из общего началаи. ''Правило треугольника'' удобно при сложении 3-х и более векторов, ''правило параллелограмма'' удобно тем, что на том же параллелограмме легко показать разность–.

II Умножение вектора на число

Произведением числа λ на вектор называют вектор, обозначаемый символомλи удовлетворяющий условиям: 1)|λ|=|λ|∙| |; 2) λ, еслиλ>0, и λ, если λ<0.

Ортом вектора называют орт^о, одинаково направленный с вектором . Очевидно, чтобы получить орт ненулевого вектора надо разделить вектор на его длину (т.е. умножить на):

III Вычитание векторов

Разность векторов определяется следующим образом

–= + (–1)∙.

В параллелограмме, построенном на векторах ии имеющих общее начало,–есть диагональ идущая из конца ''вычитаемого''

к концу ''уменьшаемого''.

.

IV Основные свойства линейных операций

Введенные выше операции обладают всеми обычными свойствами сложения и умножения чисел:

–коммутативность сложения;

–ассоциативность сложения;

–дистрибутивность умножения относительно сложения;

и т.п.

Эти свойства дают право при умножении скалярного многочлена на векторный многочлен производить умножение “почленно”.

Замечание. Согласно определению векторы иколлинеарные. Оказывается, справедливо и, в некотором смысле, обратное утверждение, а именно:

если вектор коллинеарен ненулевому вектору, то существует и притом единственное, числоλ такое, что . Попробуйте доказать это утверждение, взяв, где знак “+” соответствует, а знак “–” соответствует.

§5. Проекции вектора на оси. Направляющие косинусы

Рассмотрим некоторую ось u и выберем какой-нибудь отрезок в качестве единицы измерения длин. Если нам дан некоторый вектор , то поместим его начало в какую-нибудь точкуО оси u, а конец вектора пометим буквой А. Пусть далее В – какая-нибудь точка оси u, расположенная в положительном направлении от точки О.

Угол называют углом наклона векторак осиu. Этот угол понимаем в элементарно-геометрическом смысле, пределы изменения от 0 до π.

Проекцией вектора на осьu называют число

,

где φ – угол наклона к осиu.

Это число имеет наглядный геометрический смысл. Спроектируем начало и конец вектора на осьu, получим точки А₁,В₁. Рассмотрим вектор лежащий на осиu. Тогда

причем знак “+” соответствуем случаю, когда угол φ острый, а “–”, когда φ – тупой.

В

φ

А

А₁ В₁ u

Элементарно-геометрическими методами можно получить свойства проекций вектора на ось:

.

Замечание 1. Если φ – это угол между векторами и(понимаемый как угол между двумя отрезками, исходящими из одной точки), то числоназывают проекцией векторана направление вектора, или просто проекциейнаи обозначают символом

Пусть теперь на плоскости (или в пространстве) задана ДПСК. Проекции вектора на оси координат обозначаюта_x, a_y, a_z, или a₁, a₂, a₃, или X, Y, Z. Проекции вектора на оси координат, будучи заданы, вполне определяют его как свободный вектор, т.е. с точностью до положения в пространстве. Если вектор расположен в плоскости xOy, то достаточно двух проекций a₁ и a₂. Проекции вектора часто называют его координатами.

Тот факт, что вектор имеет проекцииa₁, a₂, a₃, показывают записью

.

Итак, впредь для нас вектор, чаще всего, это упорядоченная тройка (или пара) чисел.

Если вектор задан началомA(x₁; y₁; z₁) и концом B(x₂; y₂; z₂), то его проекции определяются формулами

т.е.

Выразим линейные операции над векторами через их проекции. Пусть ,. Тогда:

1. тогда и только тогда когда

2.

3.

4. условие коллинеарности: тогда и только тогда, когда

т.е. проекции пропорциональны;

5.

6. условие компланарности векторов ,и:

Обозначим через углы, которые векторсоставляет с осями абсцисс, ординат и аппликат соответственно. Направляющими косинусами вектораназывают косинусы этих углов. Очевидно (из определения проекций):

.

Основное свойство направляющих косинусов:

.

Кроме того, направляющие косинусы вектора служат проекциями орта этого вектора:

.

Замечание 2. Вектор можно задавать: 1) длиной и направлением (т.е. углами ); 2) началом и концом; 3) проекциями. Необходимо уметь переходить от одного способа к другому.