Конспект лекций
по разделу курса высшей математики
«АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ»
Оглавление
Раздел I Элементы линейной алгебры
Тема Матрицы и определители…………………………… 5
§1. Матрицы: основные определения…………………………… 5
§2. Основные операции над матрицами и их свойства…………… 7
§3. Линейная зависимость и независимость вектор-столбцов и
вектор-строк…………………………………………………….. 10
§4. Определители второго и третьего порядков …………………. 12
§5. Определители порядка п …………………………………….. 14
§6. Свойства определителей ……………………………………… 15
§7. Обратная матрица ……………………………………………... 19
Тема Системы линейных уравнений …………………….. 21
§1. Основные определения ………………………………………... 21
§2. Формулы Крамера для решения системы линейных
уравнений ………………………………………………………. 22
§3. Решение системы линейных уравнений с помощью
обратной матрицы ……………………………………………… 26
§4. Решение системы линейных уравнений методом Гаусса ……. 27
§5. Теорема Кронекера – Капелли …………………………………. 29
Раздел II Аналитическая геометрия
Тема Векторная алгебра ……………………………………….. 31
§1. Действительные числа. Числовая ось ………………………….. 31
§2. Системы координат ……………………………………………... 32
§3. Векторы: основные определения ……………………………….. 35
§4. Линейные операции над векторами …………………………….. 36
§5. Проекции вектора на оси. Направляющие косинусы ………….. 38
§6. Разложение вектора ………………………………………………. 40
§7. Скалярное произведение векторов ……………………………… 42
§8. Векторное произведение векторов ……………………………… 44
§9. Смешанное произведение трёх векторов ……………………….. 46
Тема Прямая на плоскости …………………………………….. 50
§1. Уравнение линии на плоскости …………………………………. 50
§2. Общее уравнение прямой на плоскости ………………………… 54
§3. Уравнения прямой с угловым коэффициентом ………………… 55
§4. Взаимное расположение двух прямых ………………………….. 58
§5. Расстояние от точки до прямой на плоскости ………………….. 59
§6. Другие формы уравнения прямой на плоскости ……………….. 60
Тема Плоскость и прямая в пространстве ………………… 64
§1. Уравнение поверхности и уравнения линии ……………………. 64
§2. Общее уравнение плоскости ……………………………………... 65
§3. Неполные уравнения плоскости …………………………………. 66
§4. Взаимное расположение двух плоскостей ………………………. 68
§5. Расстояние от точки до плоскости ……………………………….. 68
§6. Другие виды уравнения плоскости ………………………………. 69
§7. Прямая в пространстве ……………………………………………. 70
§8. Расстояние от точки до прямой в пространстве …………………. 73
§9. Взаимное расположение двух прямых в пространстве ………….. 73
§10.Взаимное расположение плоскости и прямой
в пространстве ……………………………………………………. 74
Тема Линии второго порядка …………………………………... 75
§1. Общее уравнение …………………………………………………... 75
§2. Окружность ………………………………………………………… 76
§3. Эллипс ………………………………………………………………. 77
§4. Гипербола …………………………………………………………… 79
§5. Парабола …………………………………………………………….. 82
§6. Касательные к кривым второго порядка ………………………….. 84
Литература ………………………………………………………………… 85
Приложения ……………………………………………………………….. 86
Раздел I Элементы линейной алгебры
ЛЕКЦИЯ 1
Тема Матрицы и определители
§1. Матрицы: основные понятия
Понятие матрицы возникает и используется в различных разделах высшей математики, в частности, при изучении систем линейных уравнений. В отличие от элементарной алгебры мы будем рассматривать системы с произвольным числом уравнений и неизвестных. Все неизвестные приходится обозначать одной буквой с индексом; то же относится и к свободным членам. Коэффициенты при неизвестных приходится индексировать двумя индексами: первый указывает на номер уравнения системы, а второй – на номер неизвестного, при котором находится коэффициент. Система m линейных уравнений с n неизвестными (не обязательно m=n ) запишется в следующем общем виде:
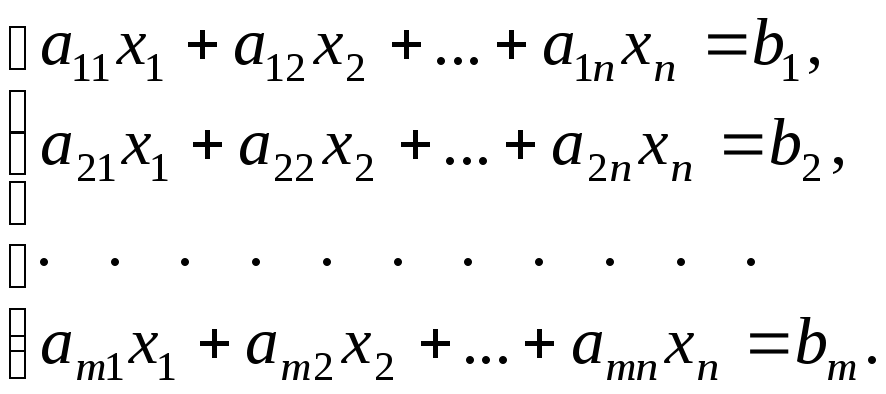(1)
Используя символ суммирования ∑, можно получить более простую запись системы:
(2)
Составленная из чисел, прямоугольная таблица вида
(3)
называется матрицей и кратко обозначается A, или (аij ), или A=(aij ) (i=1,2,…,m; j=1,2,…,n).
Числа в матрице расположены рядами. Горизонтальные ряды называются строками, а вертикальные – столбцами. Сами числа называются элементами матрицы. Индексы указывают месторасположение элемента: первый индекс указывает номер строки, второй – столбца. Заметим, что a13 следует читать “а один три”, а не “а тринадцать”. В матрице (3) m строк и
n столбцов и о ней говорят: “матрица A размера m×n” или “(m×n)-матрица A=(aij)”.
Матрица, состоящая из одного столбца (и m строк), называется вектор- столбцом, или вектором, или столбцом. Уточняя, говорят: “m-мерный столбец”.
Матрица, состоящая из одной строки ( и n столбцов), называется
n-мерной строкой, вектором, вектор-строкой.
Итак, вся информация о системе (1) содержится в двух матрицах: в матрице коэффициентов A=(aij) и столбце свободных членов B=(bi).
Если в матрице (3) m=n (т.е. число строк равно числу столбцов), то матрица называется квадратной матрицей порядка n:
(4)
Для такой матрицы вводятся понятия главной и побочной диагоналей. Главной диагональю матрицы (4) называют диагональ а11 а22 … аnn , идущая из левого верхнего угла этой матрицы в правый нижний её угол. Побочной диагональю этой матрицы называется диагональ an1 an-1,2 … a1n , идущая из левого нижнего угла в правый верхний угол.
Если все элементы матрицы (4), расположенные ниже главной диагонали, равны нулю, то матрица называется верхней треугольной. Нижняя треугольная определяется аналогично. Верхние и нижние треугольные матрицы называются также просто треугольными.
Матрица (4) называется диагональной, если она одновременно и верхняя треугольная, и нижняя, т.е. ниже и выше главной диагонали стоят нули.
Диагональная матрица, у которой все элементы, стоящие на главной диагонали равны 1, называется единичной и обозначается E, или En (индекс указывает порядок).
Матрица, у которой все элементы равны нулю, называется нулевой.
Приведем примеры, рассмотренных выше частных случаев квадратной матрицы:
,
,
,Е3=
.