
IDZ_VysshMatematTerehov
.pdf
Терехов С.В. Индивидуальные домашние задания по высшей математике
|
|
Кубы 30 чисел |
Таблица 4. |
|||
|
|
|
|
|||
N |
N 3 |
N |
N 3 |
N |
|
N 3 |
1 |
1 |
11 |
1331 |
21 |
|
9261 |
2 |
8 |
12 |
1728 |
22 |
|
10648 |
3 |
27 |
13 |
2197 |
23 |
|
12167 |
4 |
64 |
14 |
2744 |
24 |
|
13824 |
5 |
125 |
15 |
3375 |
25 |
|
15625 |
6 |
216 |
16 |
4096 |
26 |
|
17576 |
7 |
343 |
17 |
4913 |
27 |
|
19683 |
8 |
512 |
18 |
5832 |
28 |
|
21952 |
9 |
729 |
19 |
6859 |
29 |
|
24389 |
10 |
1000 |
20 |
8000 |
30 |
|
27000 |
Степени обладают следующими свойствами:
1о. a0 = 1 – по определению, a ≠ 0 ( 00 – не имеет смысла), например,
70 = 1;
2о. am = an m = n , из равенства степеней одинаковых чисел следует
равенство показателей степени;
3о. (am )n = am n , при возведении степени в степень показатели сте-
пеней перемножаются, например, (22 )3 = 22 3 = 26 = 64 ;
4о. am an = am + n , при перемножении одинаковых чисел с разными по-
казателями степеней показатели степени складываются, на-
пример, 3 10−5 4 10−7 = 12 10−5− 7 = 12 10 −12 ;
5о. aamn = am − n , при делении одинаковых чисел с разными показателями
степеней из показателя степени числа, стоящего в числителе, вычитают показатель степени числа, стоящего в знаменателе
дроби, например, |
|
3 |
10−5 |
= |
3 |
10−5 − ( − 7 ) = |
3 |
10 − 5 + 7 |
= |
3 |
10 2 |
; |
|
4 |
10−7 |
4 |
4 |
4 |
6о. (a b)m = am bm, при возведении в степень произведения разных чи-
сел каждое из чисел возводится в ту же степень, например,
(4 11)2 = 42 112 =16 121=1936;
7 |
о |
a m |
am |
, возведение в степень дроби сводится к возведению в |
||||||||||
|
. = |
bm |
||||||||||||
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
эту степень числителя и знаменателя дроби, например, |
||||||||||||||
|
|
|
|
|
|
3 |
3 |
= |
33 |
= |
27 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
5 |
53 |
125 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
10. Дробью называется рациональное число, у которого числитель дроби не делится нацело на её знаменатель:
10

Терехов С.В. Индивидуальные домашние задания по высшей математике
числитель  m знаменатель
m знаменатель  n
n
Делить на 0 нельзя,
так как выражение 03 (или ему аналогичные)
смысла не имеет.
11. Дробь называется правильной, если m<n (дробь меньше 1), в противоположном случае, когда m≥ n (дробь больше или равна 1), –
неправильной.
Пример 4. Указать, какие из приведенных дробей правильные, а какие – не-
правильные: 293 ; 1731 ; 1513 ; 52 ; 99 ; 14325 ; 1873 . Правильные дроби: 293 ; 1731 ; 52 ; 1873 .
Неправильные дроби: 1513 ; 99 = 1; 14325 .
Над дробями выполняют следующие действия:
а) сокращение дробей. Если числитель и знаменатель дроби содержат в своём разложении на простые сомножители общие множители, то числитель и знаменатель дроби можно сократить на эти
множители: |
|
30 |
= |
2 |
3 5 |
= |
2 |
; |
|
105 |
3 |
5 7 |
7 |
||||||
|
|
|
|
||||||
б) сложение (вычитание) дробей. При сложении (вычитании) дро-
бей (например, 307 + 1054 = ...? ) прежде всего, находят наименьший об-
щий знаменатель (НОЗ). Для отыскания НОЗ знаменатели дробей раскладываются на простые множители. В приведенном примере 30 = 2 3 5 и 105 = 3 5 7 . НОЗ берётся в виде произведения неповторяющихся сомножителей: НОЗ= 2 3 5 7 = 210 . Деля НОЗ на знаме-
натель первой дроби, получим дополнительный множитель к этой дроби 7. Поступая аналогично по отношению к знаменателю второй дроби, получаем дополнительный множитель к этой дроби 2. Итак,
|
7 |
2 |
|
7 7 |
|
4 2 |
|
49 + 8 |
|
|
|
19 3 |
|
|
|
|||
7 |
|
+ |
|
4 |
|
= |
+ |
= |
= |
57 |
= |
= |
19 |
. |
||||
30 |
105 |
|
210 |
210 |
210 |
210 |
70 3 |
70 |
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||
в) умножение дробей сводится к перемножению числителей и зна-
менателей дробей, причём первое произведение (числителей дробей) будет числителем, а второе произведение (знаменателей дро-
бей) – знаменателем результирующей дроби: |
2 |
|
5 |
= |
2 5 |
= |
10 |
. |
7 |
3 |
7 3 |
21 |
|||||
|
|
|
|
|
|
|
|
|
11
Терехов С.В. Индивидуальные домашние задания по высшей математике
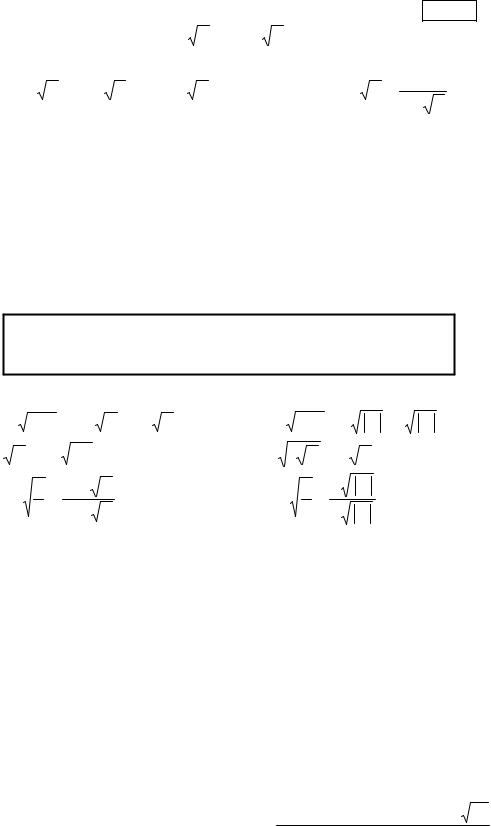
12. Числа a и b называются взаимно-обратными, если a b = 1 .
Пример 5. Являются ли числа 2 + 3 |
и 2 − 3 |
взаимно-обратными? |
|||||||
Да, потому что |
|
|
|
|
|
|
|
||
(2 + 3 ) (2 − 3 ) = 22 − ( 3) |
2= 4 − 3 = |
1, т.е. 2 + |
3 = |
1 |
. |
||||
− |
|||||||||
|
|
|
|
|
|
2 |
3 |
||
Сумма взаимно-обратных чисел удовлетворяет неравенству |
|||||||||
|
a + |
1 |
|
≥ 2 , |
|
|
|
|
|
|
|
|
|
|
|
||||
a |
|
|
|
|
|||||
|
|
|
|
|
|
|
|||
причём равенство выполняется только при a = ±1;
г) деление дробей. Для того чтобы разделить первую дробь на вто-
рую, надо 1-ую дробь умножить на перевёрнутую 2-ую дробь:
6 |
÷ |
|
5 |
= |
|
6 |
|
11 |
= |
|
6 11 |
= |
66 |
= 1 |
1 |
. |
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
13 |
11 |
13 |
5 |
13 5 |
65 |
65 |
|||||||||||||
|
|
|
|
|
|
|
|||||||||||||
Число 0 можно делить на любое другое число,
в результате получим 0.
Рассмотрим основные свойства корня n -ой степени:
1о. 2 n+ 1 a b = 2 n+ 1 a 2 n+ 1 b ; |
2о. 2 n a b = 2 n a 2 n b ; |
||||
3о. (m a )k = m ak ; |
|
|
4о. n m a = n m a ; |
||
5о. 2 n + 1 a |
= 2 n + 1 |
a |
; |
6о. 2 n a |
= 2 n a . |
b |
2 n + 1 |
b |
|
b |
2 n b |
Математические предложения часто содержат выражения, заключённые в круглые (…), квадратные […] или фигурные {…} скобки, для указания выполнения определённого порядка (приоритета) действий. Распределение действий по приоритету таковы:
– вначале выполняются действия с выражениями в скобках. При наличии разных скобок первоначально выполняют указанные действия во внутренних скобках;
– затем последовательно выполняют возведение в степень и извле- |
||||
чение при возможности корней; |
|
|
|
|
– выполняются действия умножения и деления; |
|
|
|
|
– действия сложения и вычитания выполняются последними. |
|
|||
Пример 5. Вычислить значение выражения: |
{[(9 − 22 )+ 3 5]− (4 + 2) 2 |
}− |
16 |
= ...? |
2 |
|
|
||
|
|
|
|
|
Самой внутренней скобкой является скобка (9 − 22 ), в которой надо вначале найти значение 22 = 4, а затем найти разность 9− 4 = 5. Следующей скобкой является квадратная скобка [(9 − 22 )+ 3 5]= [ 5 + 3 5 ]: вначале выполним действие умножения 3 5 =15, а затем сложения – [ 5+ 3 5] = [ 5+15] = 20. После этого выполняются: действие в оставшейся круглой скобке ( 4+2) =6 с последующим умно-
12
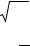
Терехов С.В. Индивидуальные домашние задания по высшей математике
жением ( 4 + 2 ) 2 = 6 2 = 12. Итак в фигурной скобке осталось выполнить действие вычитания {20 − 12 } = 8 . Вычислим числитель дроби так: 8 − 16 = 8 − 4 = 4 .
Последним действием делим числитель дроби на её знаменатель: 42 = 2 .
Ранее проведенные вычисления демонстрировали применение деятичной системы исчисления, которая использует для построения чисел цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Помимо десятичной системы исчисления в компьютерных технологиях применяют двоичную систему, в которой используются только две цифры: 0 и 1. Записать число в двоичной системе исчисления означает представить его в виде степеней числа два. Схема перевода осуществляется путём последовательного деления числа на 2 с записью остатка деления (0 или 1).
Пример 6. Перевести в двоичный код число 25. Результаты деления записываем под число справа налево:
делимое |
1 |
3 |
6 |
12 |
25 |
остаток деления (двоичный код) |
1 |
1 |
0 |
0 |
1. |
Таким образом, десятичное число 25 задаётся двоичным кодом 11001. Пример 7. Перевести двоичный код 11001 в десятичное число.
Для обратного перехода от двоичной записи к десятичному виду числа поступают так:
– под двоичным кодом записывают слева направо степени числа 2 (табл. 5)
двоичный код |
1 |
1 |
0 |
0 |
1 |
степени числа 2 |
4 |
3 |
2 |
1 |
0; |
– число 2 возводят в степени, которые стоят под 1 в двоичном коде, и результаты суммируют: 24 + 23 + 20 = 16 + 8 + 1 = 25 .
|
|
|
|
|
Таблица 5. |
|
Положительные степени числа 2. |
||||
n |
2 n |
n |
2 n |
n |
2 n |
0 |
1 |
10 |
1 024 |
20 |
1 048 576 |
1 |
2 |
11 |
2 048 |
21 |
2 097 152 |
2 |
4 |
12 |
4 096 |
22 |
4 194 304 |
3 |
8 |
13 |
8 192 |
23 |
8 388 608 |
4 |
16 |
14 |
16 384 |
24 |
16 777 216 |
5 |
32 |
15 |
32 768 |
25 |
33 554 432 |
6 |
64 |
16 |
65 536 |
26 |
67 108 864 |
7 |
128 |
17 |
131 072 |
27 |
134 217 728 |
8 |
256 |
18 |
262 144 |
28 |
268 435 456 |
9 |
512 |
19 |
524 288 |
29 |
536 870 912 |
Дробное число переводят в двоичную запись путём вычитания из числа последовательности отрицательных степеней 2 (см. табл. 6). Процесс продолжается до полного исчерпания десятичного числа.
13
Терехов С.В. Индивидуальные домашние задания по высшей математике
Таблица 6.
Отрицательные степени числа 2.
n |
2 n |
n |
2 n |
–1 |
0,5 |
–11 |
0,00048828125 |
–2 |
0,25 |
–12 |
0,000244140625 |
–3 |
0,125 |
–13 |
0,0001220703125 |
–4 |
0,0625 |
–14 |
0,00006103515625 |
–5 |
0,03125 |
–15 |
0,000030517578125 |
–6 |
0,01562 |
–16 |
0,0000152587890625 |
–7 |
0,0078125 |
–17 |
0,00000762939453125 |
–8 |
0,00390625 |
–18 |
0,000003814697265625 |
–9 |
0,001953125 |
–19 |
0,0000019073486328125 |
–10 |
0,0009765625 |
–20 |
0,00000095367431640625 |
Пример 8. Перевести число 0,40625 в двоичный код.
–если вычитание 0,5 (степень n= –1) невозможно, то после запятой ставим 0 и переходим к следующей степени (0,25 при n= –2); если вычитание возможно, то ставим 1;
–описанный процесс представления десятичной дроби в двоичной системе исчисления продолжается до тех пор, пока в остатке не получится 0, или до достижения установленной точности представления:
|
_ 0,40625 |
Двоичный код |
|||
(n=-1) |
|
0,5 (нельзя – после запятой ставим 0) |
0,01101 |
||
|
_ |
0,40625 |
|
|
|
(n=-2) |
|
0,25 (можно – ставим 1) |
|
||
|
|
||||
|
_ |
0,15625 |
|
|
|
(n=-3) |
0,125 (можно – ставим 1) |
|
|||
|
_ |
0,03125 |
|
|
|
(n=-4) |
|
0,0625 (нельзя –ставим 0) |
|
||
|
_ 0,03125 |
|
|||
(n=-5) |
|
0,03125(можно – ставим 1) |
|
||
Пример 9. Перевести двоичный код 0,01101 в десятичное число.
Переход осуществляется также как и для целых чисел, пишутся отрицательные степени под числом, но слева направо; затем 2 возводится в те степени, которые расположены под единицами:
двоичный код |
0, |
0 |
1 |
1 |
0 |
1 |
степени числа 2 |
0 |
-1 |
-2 |
-3 |
-4 |
-5; |
результаты складываются: 2−2 + 2−3 + 2−5 = 0, 25 + 0,125 + 0, 03125 = 0, 40625 .
13. Арифметической прогрессией называется такая последовательность чисел a1, a2 ,..., an , …, у которой разность d между предыдущим
и последующим членами прогрессии постоянна:
a2 − a1 = a3 − a2 = a4 − a3 = ... = an − an−1 = ... = d .
Пример 10. Является ли последовательность чётных чисел 2, 4, 6,... арифметической прогрессией?
14
Терехов С.В. Индивидуальные домашние задания по высшей математике
Да, является, так как разность между предыдущим и последующим членами последовательности постоянна и равна d = 2 .
Если известен первый член арифметической прогрессии a1 и
её разность d , то любой член последовательности вычисляется по формуле: an = a1 + (n − 1) d .
Пример 11. Вычислить седьмой член арифметической прогрессии для последовательности чётных чисел.
Так как для последовательности чётных чисел первый член прогрессии равен a1 = 2 , а разность d = 2 , то седьмой член прогрессии равен a7 = 2 + 6 2 = 14 .
Основное свойство арифметической прогрессии:
каждый её член равен полусумме его соседних членов,
т.е. an = an− 1 + an+ 1 .
2
Для нахождения суммы n первых членов арифметической прогрес-
сии применяют формулу: |
|
an + a1 |
n |
или |
|
|
(n − 1) d |
n |
. |
||
Sn = |
|
Sn = a1 |
+ |
|
|
||||||
2 |
2 |
||||||||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
14. Геометрической прогрессией называется такая последовательность чисел a1, a2 , ..., an , …, для которой отношение прогрессии q
последующего члена к предыдущему есть величина постоянная:
|
a |
2 |
= |
a |
3 |
= ... = |
a n |
= ... = q |
. |
|
a1 |
a2 |
an− 1 |
||||||
|
|
|
|
|
|||||
Пример 12. Является ли последовательность чисел -2, 4, -8, 16, -32,... геометрической прогрессией.
Да, является, так как её знаменатель q = |
4 |
|
= |
− 8 |
= |
16 |
= |
− 32 |
= −2 . |
|
− 2 |
4 |
− 8 |
16 |
|||||||
|
|
|
|
|
||||||
Согласно определению, a2 = a1 q; |
a3 = a2 q = a1 q2; a4 = a3 q = a1 q3 ; …, |
|||||||||
т.е. любой член геометрической прогрессии вычисляется по формуле: an
Каждый член знакоположительной геометрической прогрессии
равен среднему геометрическому от его соседних членов,
т.е. an =  an− 1 an+ 1 .
an− 1 an+ 1 .
Сумма n |
первых членов геометрической прогрессии находится |
||||||||||
по формуле: |
Sn = |
a 1 |
(1 − qn ) |
(q ≠ 1) |
. Если |
|
q |
|
<1, то сумма бесконечной |
||
|
|
||||||||||
|
1 − q |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
геометрической прогрессии равна |
|
a |
. |
||||||||
S = |
1 |
|
|||||||||
1 − q |
|||||||||||
15

Терехов С.В. Индивидуальные домашние задания по высшей математике
Пример 13. Вычислить сумму бесконечной геометрической прогрессии при
a1 = |
1 |
и q = − |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
1 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
1 |
|
|
Сумма бесконечной геометрической прогрессии равна S = |
|
2 |
|
|
|
= |
|
= |
. |
|||||||
|
|
1 |
|
2 |
3 |
3 |
||||||||||
|
|
|
1 |
− − |
|
|
|
|
|
|
|
|
||||
|
|
|
2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
15. Одночленом называется произведение числового множителя на
одну или несколько букв: − 2 a b; |
1 x2 y z; 2 d; l x; − 0.5 . |
|
3 |
16.Многочленом (полиномом или целым алгебраическим выраже-
нием) называется сумма одночленов: ax2 + bx + c; 3x − y .
17.Члены полинома, отличающиеся только числовым множителем или равные между собой, называются подобными.
18.Приведением подобных членов называется замена нескольких подобных слагаемых одним выражением, коэффициент при кото-
ром равен алгебраической сумме коэффициентов при подобных слагаемых:
2x3 − 3x2 + 6x − 5 + ax3 − bx2 − 4x + 6 = (2 + a)x3 − (3 + b)x2 + 2x + 1.
В дальнейшем числовые коэффициенты будем обозначать на-
чальными буквами латинского алфавита a , b , c , d ,... , а неизвестные переменные величины – последними буквами этого алфавита
s, t, u, v, w, x, y, z .
Все последующие рассуждения будем проводить по отношению к полиномам вида
|
|
|
|
|
|
Pn (x) = an xn + an−1 xn− 1 + ...+ a2 x2 + a1 x + a0 |
, |
|
|
|
||||||
где числовые множители an , an−1, …, |
a 2 , a1, |
a0 |
R , x – переменная |
|||||||||||||
неизвестная, а n N – называется порядком полинома: |
|
|
|
|||||||||||||
P0 ( x) = − 2 |
и Q0 ( x) = a – полиномы нулевого порядка; |
|
|
|
||||||||||||
P1(x) = ax+ b – полином первого порядка (линейный полином); |
||||||||||||||||
P2 ( x) = ax 2 + bx + c – полином второго порядка и т.д. |
|
|
|
|||||||||||||
19. Полином вида |
|
|
|
|
|
|
|
|
|
|
||||||
a |
n |
xn + a |
n |
−1 |
xn −1 y + a |
n − 2 |
xn − 2 y2 + ... + a |
2 |
x2 yn − 2 |
+ a x yn − 1 |
+ a |
0 |
yn |
|||
|
|
|
|
|
|
|
1 |
|
|
|
||||||
называется однородным многочленом двух переменных.
Следует обратить внимание на то, что сумма показателей степе-
ни в произведении неизвестных есть величина неизменная для однородного многочлена.
Рассмотрим арифметические действия над полиномами:
16
Терехов С.В. Индивидуальные домашние задания по высшей математике
– при сложении (вычитании) полиномов после приведения подобных членов получают полином, порядок которого равен высшему порядку многочлена, входящего в сумму.
Пример 14. Найти сумму полинома второй степени P2 (x) = 2x2 − 3x + 4 и многочлена первого порядка P1(x) = 6x − 7 .
Результирующим многочленом будет полином второго порядка
Q2 (x) = P2 (x) + P1 (x) = 2x2 − 3x + 4 + 6x − 7 = 2x2 + (−3 + 6)x + (4 − 7) = 2x2 + 3x − 3 .
– при умножении одного многочлена на другой получается полином, степень которого равна сумме порядков полиномов, входящих в произведение, получаемое путём умножения каждого одночле-
на первого многочлена на каждый одночлен второго полинома и приведения подобных членов.
Пример 15. Найти произведение полиномов P2 (x) = 2x2 − 3x + 4 и P1 (x) = 6 x − 7 .
В результате произведения получим полином
Q3 (x) = P2 (x)P1 (x) = (2x2 − 3x + 4)(6x − 7) = 2x2 6x + 2x2 (−7) − 3x 6x − 3x (−7) + 4 6x +
+4 (−7) = 12x3 − 14x2 − 18x2 + 21x + 24x − 28 = 12x3 − 32x2 + 45x − 28.
Вопределённых случаях для перемножения полиномов приме-
няют формулы сокращённого умножения:
1) |
(a + b) 2 = a 2 + 2ab + b 2 – квадрат суммы |
|||
|
( x + 1)2 = ( x )2 + 2 |
x 1+ 12 = x + 2 x + 1; |
||
|
(x + 2) 2 = (x) 2 + 2 x 2 + 22 = x2 + 4 x + 4 ; |
|||
2) |
( a − b ) 2 = a 2 − 2 a b + b 2 – квадрат разности |
|||
|
(3 − x)2 = 32 − 2 3 x + x2 = 9 − 6x + x2 ; |
|||
(2x − 5)2 = (2x)2 − 2 2x 5 + 52 = 4x2 − 20x + 25; |
||||
3) |
(a + b)3 = a3 + 3a2b + 3ab2 + b3 – куб суммы |
|||
4) |
(3x + 1)3 = (3x)3 + 3 (3x)2 1 + 3 3x 12 + 13 = 27x3 + 27x2 + 9x + 1; |
|||
(a − b)3 = a3 − 3a2b + 3ab2 − b3 – куб разности |
||||
|
(2 − x)3 = 23 − 3 22 x + 3 2 x2 − x3 = 8 − 12x + 6x2 − x3 ; |
|||
5) |
a2 − b2 = (a − b) (a + b) |
– разность квадратов |
||
|
x2 − 4 = x 2 − 2 2 = (x − 2) (x + 2) ; |
|
||
|
3 − x = ( 3 )2 − ( |
x )2 = ( 3 − x ) ( 3 + x ); |
||
6) |
a3 − b3 = (a − b) (a2 + ab + b2 ) – разность кубов |
|||
|
(x − 2) (x2 + 2x + 4) = x3 − 23 = x3 − 8 ; |
|||
7) a3 + b3 = (a + b) (a2 − ab + b2 ) – сумма кубов |
||||
|
8x3 + 27 = (2x) 3 + 3 3 = (2x + 3) (4x2 − 6x + 9) ; |
|||
8) a4 − b4 = (a − b) (a + b) (a2 + b2 ) |
– разность квартетов; |
|||
9) a4 + b4 = (a2 + |
2 a b + b2 ) (a2 − |
2 a b + b2 ) – сумма квартетов; |
||
17

Терехов С.В. Индивидуальные домашние задания по высшей математике
– при делении полиномов возникают дроби вида Pn (x) , при этом
Qm (x)
исключаются те значения переменной x , при которых знаменатель дроби обращается в нуль (Qm (x) = 0 – корни этого уравнения исклю-
чаются из рассмотрения в силу того, что делить на 0 нельзя).
20. Отношение полиномов Pn (x) называется рациональной дробью.
Qm (x)
21. Если порядок многочлена, стоящего в числителе дроби, меньше степени полинома, стоящего в знаменателе дроби (n < m), то дробь называется правильной, в противном случае ( n ≥ m ) – дробь называ-
ется неправильной.
Пример 16. Определить, какие из приведенных рациональных дробей являются правильными, а какие – неправильными:
а)
б)
в)
|
|
|
|
|
|
|
|
|
|
|
2x − 3 |
|
; |
|
x3 |
; |
3x4 − 5x2 + 7 |
? |
|
|
|
|
|
|
|
|
|
3x2 − 4x + 5 |
|
|
x3 − 8 |
|
x − 2 |
||||
2x − 3 |
= |
|
|
P1 (x) |
n = 1; |
n < m – правильная рациональная дробь; |
||||||||||||
3x2 − 4x + 5 |
|
Q2 (x) |
|
m = 2, |
||||||||||||||
x3 |
P3 (x) |
|
|
n = 3; |
|
– неправильная рациональная дробь; |
||||||||||||
|
= |
|
|
|
|
m = 3, n = m |
||||||||||||
x3 − 8 |
Q (x) |
|
|
|||||||||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x4 − 5x2 + |
7 |
= |
|
P4 (x) |
n = 4; |
n > m – неправильная рациональная дробь. |
||||||||||||
x − 2 |
|
|
Q (x) |
m = 1, |
||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
Если рациональная числовая дробь неправильная, то можно выделить целую часть так же.
Пример 17. Выделить целую часть и правильную рациональную дробь у чис-
ла 2573 = …?
Разделим числитель дроби на её знаменатель:
_ 257 3 – знаменатель дроби
24 85 – целая часть
_ 17 15
2 – остаток деления
2573 = 85 + 23 или в сокращённом виде 2573 = 85 23 .
При делении полинома на полином надо обращать внимание на старшие степени полиномов и числовые множители при них.
Пример 18. Выделить “целую” часть у неправильной рациональной дроби
P (x) |
|
3x4 − 5x2 + 7 |
= …? |
4 |
= |
|
|
Q (x) |
x − 2 |
||
1 |
|
|
|
18

Терехов С.В. Индивидуальные домашние задания по высшей математике
Итак, _ 3x4 − 5x2 + 7 |
|
x − 2 – знаменатель дроби |
|
|
|
|
|||||||||||
|
3x4 − 6x3 |
|
|
3x3 + 6x2 + 7x + 14 – “целая” часть |
|||||||||||||
|
_ 6x3 − 5x2 + 7 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
6x3 − 12x2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
_ 7x2 + 7 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
7x2 − 14x |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
_ 14x + 7 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
14x − 28 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
35 |
– остаток деления |
||||||||
|
|
|
|
|
3x4 − 5x2 + 7 |
= 3x |
3 |
+ 6x |
2 |
+ 7x + 14 |
35 |
|
. |
||||
|
|
|
|
|
|
x − 2 |
|
|
+ |
|
|
||||||
|
|
|
|
|
|
|
|
x − 2 |
|||||||||
Деление числителя на знаменатель дроби прекращается тогда, когда в остатке деления получается полином, порядок которого ста-
новится меньше порядка полинома, стоящего в знаменателе.
Таким образом, если математическое предложение содержит рациональные дроби, то с ними выполняются те же действия, что и над обычными дробями. Отличие состоит в том, что надо исклю-
чать из рассмотрения те значения переменной x , при которых знаменатель дроби обращается в 0.
Если пример содержит несколько дробей, то все дроби надо привести к наименьшему общему знаменателю (НОЗ), для чего зна-
менатели дробей раскладываются на простые множители и НОЗ
берётся в виде произведения неповторяющихся сомножителей.
Пример 19. Найти НОЗ и дополнительные множители для дробей
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 x |
|
− 2 x + 1 |
= |
|
1 |
|
|
. |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x + 2 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 − x |
|
2 − |
4 |
|
|
|
|
|
|
|
|
|
|||||||||
В этой задаче знаменатели дробей равны |
|
|
|
|
|
|
3x |
|
2x + 1 |
|
|
|
|
|
|
||||||||||||||||||||||
|
3x |
|
− |
2x + 1 |
|
= |
|
1 |
|
|
|
3x |
− |
2x + 1 |
= |
|
1 |
|
|
|
|
|
+ |
= |
|
1 |
|
|
|||||||||
|
x + |
2 |
2 − x |
|
x2 − 4 |
|
x + 2 |
− (x − 2) |
x |
2 − 4 |
|
x + 2 |
|
(x − 2) (x + 2) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x − 2 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x + 2 , |
x − 2 и x2 − 4 = (x − 2)(x + 2) , |
|
|
|
|
|||||||||||||||||||
отсюда видно, |
что произведение (x − 2)(x + 2) |
является НОЗ. Поступая так же, |
|||||||||||||||||||||||||||||||||||
как и при суммировании обычных дробей, получаем |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
x − 2 |
x + 2 |
1 |
|
|
|
3x (x − 2) |
|
(2x + 1) (x + 2) |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
3x |
+ |
|
2x + 1 |
= |
|
1 |
|
|
|
|
|
+ |
= |
1 |
, |
|
||||||||||||||||
|
|
|
|
|
x + 2 |
|
|
x − 2 |
(x − 2) (x + 2) |
|
|
x2 − 4 |
|
|
|
|
x2 − 4 |
|
x2 − 4 |
|
|
||||||||||||||||
при этом x − 2 ≠ 0, x + 2 ≠ 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
Разложение полиномов на простые сомножители применяется |
|||||||||||||||||||||||||||||||||||
при решении различных задач. Если x1, x2 ,..., xn |
– вещественные кор- |
||||||||||||||||||||||||||||||||||||
ней уравнения Pn(x) = 0, то полином можно представить в виде произ-
19
