IDZ_VysshMatematTerehov

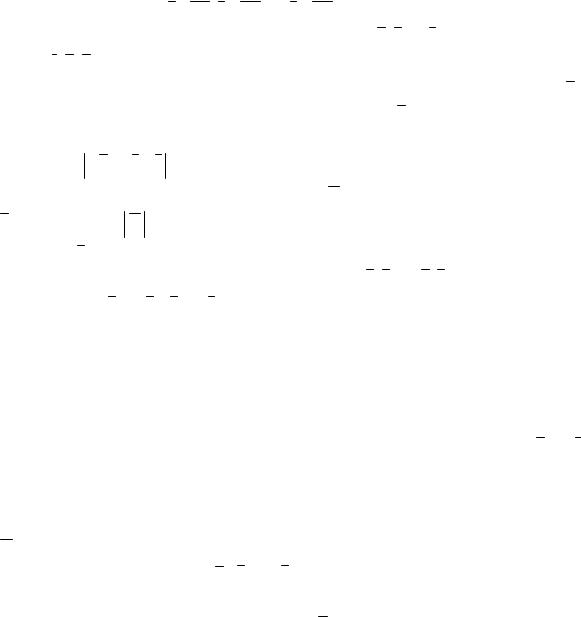
Терехов С.В. Индивидуальные домашние задания по высшей математике

Задания для самостоятельного решения

II. Элементы векторной алгебры

Вариант 2

Даны четыре точки A ( 2; 0; 1 ), B ( − 1; 1; 0 ) , C (0; − 1; − 2 ) и D (1; 1; 0 ):

1.Найти векторы a = AB, b = AC и c = AD. Имеются ли среди них коллинеарные? Записать разложение векторов a, b и c по декартовому базису (i, j, k ).

2.Найти единичный вектор того же направления что и вектор a .

3.Найти направляющие косинусы вектора a . Сравнить с ответом в предыдущем пункте. Сделать выводы.

4.Найти 2 a − 3b + c .

5.Определить координаты вектора X = ( x; y; z) , коллинеарного вектору a , зная, что X = 5 и он направлен в сторону, противоположную

вектору a .

6.Вычислить скалярные произведения a b и a c . Перпендикулярны

ли векторы a и b , a и c между собой?

7.Найти внутренний угол при вершине A и внешний угол при вершине C треугольника ABC .

10. Найти единичный вектор, перпендикулярный векторам a и b .

F = ( 2; − 1; 3 ) , приложенной к точке A относительно точки C .

13.Лежат ли векторы a , b и c в одной плоскости? Могут ли эти

векторы образовать базис пространства и почему? Если могут, то разложить по этому базису вектор d = (1; − 1; 5 ) .

14.Чему равны объём пирамиды с вершинами A, B , C , D и её высота, опущенная из точки A на основание BCD ?

90

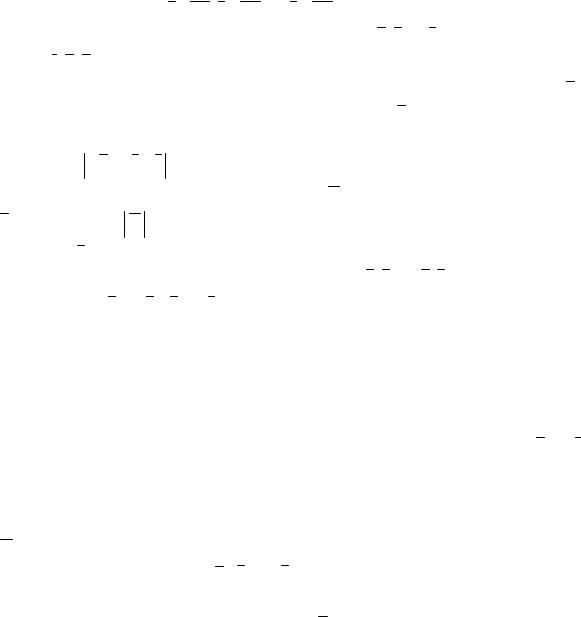
Терехов С.В. Индивидуальные домашние задания по высшей математике

Задания для самостоятельного решения

II. Элементы векторной алгебры

Вариант 3

Даны четыре точки A (1; 2; 0 ) , B ( 0; 1; 1 ) , C ( 0; 1; 2 ) и D ( 0; 1; − 1 ):

1.Найти векторы a = AB, b = AC и c = AD. Имеются ли среди них коллинеарные? Записать разложение векторов a, b и c по декартовому базису (i, j, k ).

2.Найти единичный вектор того же направления что и вектор a .

3.Найти направляющие косинусы вектора a . Сравнить с ответом в предыдущем пункте. Сделать выводы.

4.Найти 2 a − 3b + c .

5.Определить координаты вектора X = ( x; y; z) , коллинеарного вектору a , зная, что X = 5 и он направлен в сторону, противоположную

вектору a .

6.Вычислить скалярные произведения a b и a c . Перпендикулярны

ли векторы a и b , a и c между собой?

7.Найти внутренний угол при вершине A и внешний угол при вершине C треугольника ABC .

10. Найти единичный вектор, перпендикулярный векторам a и b .

F = ( 2; − 1; 3 ) , приложенной к точке A относительно точки C .

13.Лежат ли векторы a , b и c в одной плоскости? Могут ли эти

векторы образовать базис пространства и почему? Если могут, то разложить по этому базису вектор d = (1; − 1; 5 ) .

14.Чему равны объём пирамиды с вершинами A, B , C , D и её высота, опущенная из точки A на основание BCD ?

91

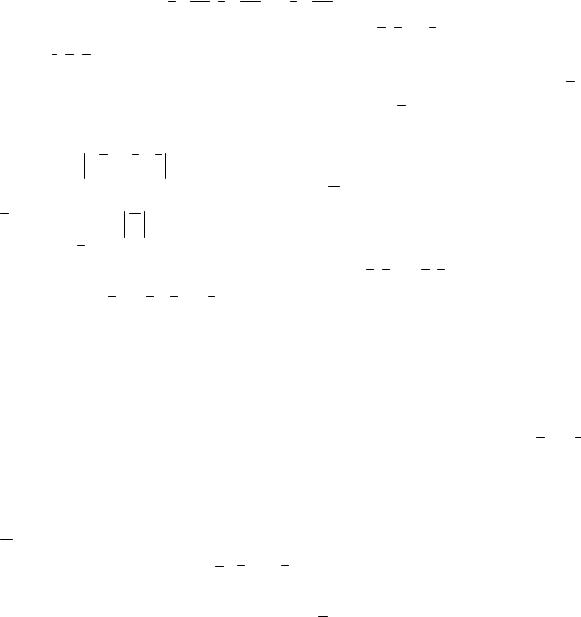
Терехов С.В. Индивидуальные домашние задания по высшей математике

Задания для самостоятельного решения

II. Элементы векторной алгебры

Вариант 4

Даны четыре точки A ( − 1;0; 2 ) , B (1; − 2; 0 ) , C (1; − 1; 0 ) и D ( 0; 1; 1 ):

1.Найти векторы a = AB, b = AC и c = AD. Имеются ли среди них коллинеарные? Записать разложение векторов a, b и c по декартовому базису (i, j, k ).

2.Найти единичный вектор того же направления что и вектор a .

3.Найти направляющие косинусы вектора a . Сравнить с ответом в предыдущем пункте. Сделать выводы.

4.Найти 2 a − 3b + c .

5.Определить координаты вектора X = ( x; y; z) , коллинеарного вектору a , зная, что X = 5 и он направлен в сторону, противоположную

вектору a .

6.Вычислить скалярные произведения a b и a c . Перпендикулярны

ли векторы a и b , a и c между собой?

7.Найти внутренний угол при вершине A и внешний угол при вершине C треугольника ABC .

10. Найти единичный вектор, перпендикулярный векторам a и b .

F = ( 2; − 1; 3 ) , приложенной к точке A относительно точки C .

13.Лежат ли векторы a , b и c в одной плоскости? Могут ли эти

векторы образовать базис пространства и почему? Если могут, то разложить по этому базису вектор d = (1; − 1; 5 ) .

14.Чему равны объём пирамиды с вершинами A, B , C , D и её высота, опущенная из точки A на основание BCD ?

92

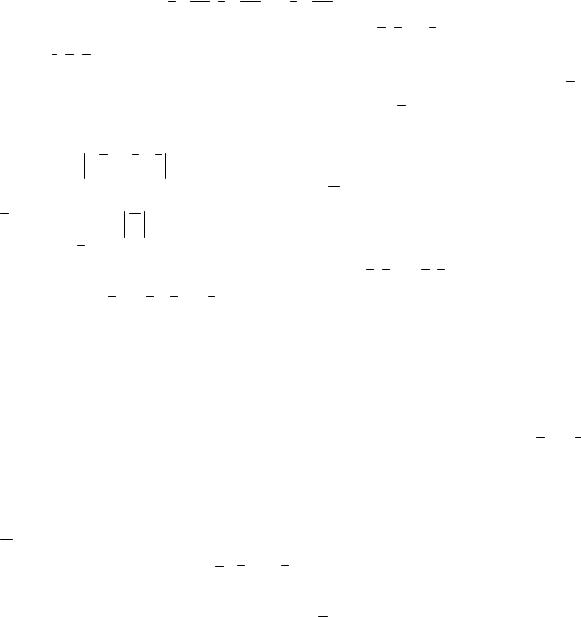
Терехов С.В. Индивидуальные домашние задания по высшей математике

Задания для самостоятельного решения

II. Элементы векторной алгебры

Вариант 5

Даны четыре точки A (0; 2; − 1 ) , B ( 0; 1; − 1 ) , C ( − 1; 0; 1 ) и D ( − 1; 0; 2 ):

1.Найти векторы a = AB, b = AC и c = AD. Имеются ли среди них коллинеарные? Записать разложение векторов a, b и c по декартовому базису (i, j, k ).

2.Найти единичный вектор того же направления что и вектор a .

3.Найти направляющие косинусы вектора a . Сравнить с ответом в предыдущем пункте. Сделать выводы.

4.Найти 2 a − 3b + c .

5.Определить координаты вектора X = ( x; y; z) , коллинеарного вектору a , зная, что X = 5 и он направлен в сторону, противоположную

вектору a .

6.Вычислить скалярные произведения a b и a c . Перпендикулярны

ли векторы a и b , a и c между собой?

7.Найти внутренний угол при вершине A и внешний угол при вершине C треугольника ABC .

10. Найти единичный вектор, перпендикулярный векторам a и b .

F = ( 2; − 1; 3 ) , приложенной к точке A относительно точки C .

13.Лежат ли векторы a , b и c в одной плоскости? Могут ли эти

векторы образовать базис пространства и почему? Если могут, то разложить по этому базису вектор d = (1; − 1; 5 ) .

14.Чему равны объём пирамиды с вершинами A, B , C , D и её высота, опущенная из точки A на основание BCD ?

93

Терехов С.В. Индивидуальные домашние задания по высшей математике

Задания для самостоятельного решения

II. Элементы векторной алгебры

Вариант 6

Даны четыре точки A (2; − 1; 0 ) , B (1; 1; 0 ) , C ( − 1; 2; 0 ) и D (1; − 1; 1 ) :

1.Найти векторы a = AB, b = AC и c = AD. Имеются ли среди них коллинеарные? Записать разложение векторов a, b и c по декартовому базису (i, j, k ).

2.Найти единичный вектор того же направления что и вектор a .

3.Найти направляющие косинусы вектора a . Сравнить с ответом в предыдущем пункте. Сделать выводы.

4.Найти 2 a − 3b + c .

5.Определить координаты вектора X = ( x; y; z) , коллинеарного вектору a , зная, что X = 5 и он направлен в сторону, противоположную

вектору a .

6.Вычислить скалярные произведения a b и a c . Перпендикулярны

ли векторы a и b , a и c между собой?

7.Найти внутренний угол при вершине A и внешний угол при вершине C треугольника ABC .

10. Найти единичный вектор, перпендикулярный векторам a и b .

F = ( 2; − 1; 3 ) , приложенной к точке A относительно точки C .

13.Лежат ли векторы a , b и c в одной плоскости? Могут ли эти

векторы образовать базис пространства и почему? Если могут, то разложить по этому базису вектор d = (1; − 1; 5 ) .

14.Чему равны объём пирамиды с вершинами A, B , C , D и её высота, опущенная из точки A на основание BCD ?

94

Терехов С.В. Индивидуальные домашние задания по высшей математике

Задания для самостоятельного решения

II. Элементы векторной алгебры

Вариант 7

Даны четыре точки A (1; 1; 0 ) , B (2; − 1; 0 ) , C ( 0; 1; − 1 ) и D ( 0; 1; − 2 ) :

1.Найти векторы a = AB, b = AC и c = AD. Имеются ли среди них коллинеарные? Записать разложение векторов a, b и c по декартовому базису (i, j, k ).

2.Найти единичный вектор того же направления что и вектор a .

3.Найти направляющие косинусы вектора a . Сравнить с ответом в предыдущем пункте. Сделать выводы.

4.Найти 2 a − 3b + c .

5.Определить координаты вектора X = ( x; y; z) , коллинеарного вектору a , зная, что X = 5 и он направлен в сторону, противоположную

вектору a .

6.Вычислить скалярные произведения a b и a c . Перпендикулярны

ли векторы a и b , a и c между собой?

7.Найти внутренний угол при вершине A и внешний угол при вершине C треугольника ABC .

10. Найти единичный вектор, перпендикулярный векторам a и b .

F = ( 2; − 1; 3 ) , приложенной к точке A относительно точки C .

13.Лежат ли векторы a , b и c в одной плоскости? Могут ли эти

векторы образовать базис пространства и почему? Если могут, то разложить по этому базису вектор d = (1; − 1; 5 ) .

14.Чему равны объём пирамиды с вершинами A, B , C , D и её высота, опущенная из точки A на основание BCD ?

95

Терехов С.В. Индивидуальные домашние задания по высшей математике

Задания для самостоятельного решения

II. Элементы векторной алгебры

Вариант 8

Даны четыре точки A ( 0; 1; 1 ) , B (1; − 1; 0 ), C (1; 0; 2 ) и D ( − 1; − 1; 0 ):

1.Найти векторы a = AB, b = AC и c = AD. Имеются ли среди них коллинеарные? Записать разложение векторов a, b и c по декартовому базису (i, j, k ).

2.Найти единичный вектор того же направления что и вектор a .

3.Найти направляющие косинусы вектора a . Сравнить с ответом в предыдущем пункте. Сделать выводы.

4.Найти 2 a − 3b + c .

5.Определить координаты вектора X = ( x; y; z) , коллинеарного вектору a , зная, что X = 5 и он направлен в сторону, противоположную

вектору a .

6.Вычислить скалярные произведения a b и a c . Перпендикулярны

ли векторы a и b , a и c между собой?

7.Найти внутренний угол при вершине A и внешний угол при вершине C треугольника ABC .

10. Найти единичный вектор, перпендикулярный векторам a и b .

F = ( 2; − 1; 3 ) , приложенной к точке A относительно точки C .

13.Лежат ли векторы a , b и c в одной плоскости? Могут ли эти

векторы образовать базис пространства и почему? Если могут, то разложить по этому базису вектор d = (1; − 1; 5 ) .

14.Чему равны объём пирамиды с вершинами A, B , C , D и её высота, опущенная из точки A на основание BCD ?

96

Терехов С.В. Индивидуальные домашние задания по высшей математике

Задания для самостоятельного решения

II. Элементы векторной алгебры

Вариант 9

Даны четыре точки A ( − 1; 1; 0 ) , B ( − 1; − 1; 1 ) , C ( 0; − 1; 1 ) и D (1; 0; 2 ) :

1.Найти векторы a = AB, b = AC и c = AD. Имеются ли среди них коллинеарные? Записать разложение векторов a, b и c по декартовому базису (i, j, k ).

2.Найти единичный вектор того же направления что и вектор a .

3.Найти направляющие косинусы вектора a . Сравнить с ответом в предыдущем пункте. Сделать выводы.

4.Найти 2 a − 3b + c .

5.Определить координаты вектора X = ( x; y; z) , коллинеарного вектору a , зная, что X = 5 и он направлен в сторону, противоположную

вектору a .

6.Вычислить скалярные произведения a b и a c . Перпендикулярны

ли векторы a и b , a и c между собой?

7.Найти внутренний угол при вершине A и внешний угол при вершине C треугольника ABC .

10. Найти единичный вектор, перпендикулярный векторам a и b .

F = ( 2; − 1; 3 ) , приложенной к точке A относительно точки C .

13.Лежат ли векторы a , b и c в одной плоскости? Могут ли эти

векторы образовать базис пространства и почему? Если могут, то разложить по этому базису вектор d = (1; − 1; 5 ) .

14.Чему равны объём пирамиды с вершинами A, B , C , D и её высота, опущенная из точки A на основание BCD ?

97

Терехов С.В. Индивидуальные домашние задания по высшей математике

Задания для самостоятельного решения

II. Элементы векторной алгебры

Вариант 10

Даны четыре точки A( − 1; 0; 1 ) , B (1; − 1; − 2 ) , C (1; − 1; 0 ) и D (1; 0; −1):

1.Найти векторы a = AB, b = AC и c = AD. Имеются ли среди них коллинеарные? Записать разложение векторов a, b и c по декартовому базису (i, j, k ).

2.Найти единичный вектор того же направления что и вектор a .

3.Найти направляющие косинусы вектора a . Сравнить с ответом в предыдущем пункте. Сделать выводы.

4.Найти 2 a − 3b + c .

5.Определить координаты вектора X = ( x; y; z) , коллинеарного вектору a , зная, что X = 5 и он направлен в сторону, противоположную

вектору a .

6.Вычислить скалярные произведения a b и a c . Перпендикулярны

ли векторы a и b , a и c между собой?

7.Найти внутренний угол при вершине A и внешний угол при вершине C треугольника ABC .

10. Найти единичный вектор, перпендикулярный векторам a и b .

F = ( 2; − 1; 3 ) , приложенной к точке A относительно точки C .

13.Лежат ли векторы a , b и c в одной плоскости? Могут ли эти

векторы образовать базис пространства и почему? Если могут, то разложить по этому базису вектор d = (1; − 1; 5 ) .

14.Чему равны объём пирамиды с вершинами A, B , C , D и её высота, опущенная из точки A на основание BCD ?

98

Терехов С.В. Индивидуальные домашние задания по высшей математике

Задания для самостоятельного решения

II. Элементы векторной алгебры

Вариант 11

Даны четыре точки A (1; −1; 0 ), B( 0; − 2; − 1 ) , C ( − 1; − 1; 0 ) и D ( 0; 1; − 1 ):

1.Найти векторы a = AB, b = AC и c = AD. Имеются ли среди них коллинеарные? Записать разложение векторов a, b и c по декартовому базису (i, j, k ).

2.Найти единичный вектор того же направления что и вектор a .

3.Найти направляющие косинусы вектора a . Сравнить с ответом в предыдущем пункте. Сделать выводы.

4.Найти 2 a − 3b + c .

5.Определить координаты вектора X = ( x; y; z) , коллинеарного вектору a , зная, что X = 5 и он направлен в сторону, противоположную

вектору a .

6.Вычислить скалярные произведения a b и a c . Перпендикулярны

ли векторы a и b , a и c между собой?

7.Найти внутренний угол при вершине A и внешний угол при вершине C треугольника ABC .

10. Найти единичный вектор, перпендикулярный векторам a и b .

F = ( 2; − 1; 3 ) , приложенной к точке A относительно точки C .

13.Лежат ли векторы a , b и c в одной плоскости? Могут ли эти

векторы образовать базис пространства и почему? Если могут, то разложить по этому базису вектор d = (1; − 1; 5 ) .

14.Чему равны объём пирамиды с вершинами A, B , C , D и её высота, опущенная из точки A на основание BCD ?

99