Алгоритм прямого ходу методу Гаусса

1. У першому рядку першому стовпці обирають ключовий елемент, що відрізняється від нуля (у разі необхідності слід поміняти місцями рядки розширеної матриці).

2. Перший рядок переписують без змін. Під ключовим елементом записують нулі. Інші елементи обчислюють за правилом прямокутника. Для цього кожен елемент, що потребує розрахунку, з’єднують з першим рядком і першим стовпцем і також з ключовим елементом. Розраховане значення елементу дорівнює різниці між добутком елементів діагоналі, яка містить ключовий елемент, і добутком елементів іншої діагоналі згідно схеми:

Тут  ключовий елемент;  елемент, що розраховується;  нове значення елементу :.

3. Далі за ключовий елемент обирають ненульовий елемент другого рядка і другого стовпця. Перший і другий стовпці доповнюють нулями.

4. Процедуру повторюють до приведення розширеної матриці до трикутного вигляду.

Для реалізації оберненого ходу за видом одержаної розширеної матриці виписують систему рівнянь і далі одержують загальний розв’язок.

Приклад 1.11.

Розв’язати методом Гаусса систему лінійних рівнянь:

Розв’язання. Раніше для цієї системи було доведено її сумісність. Прямий хід  приведемо розширену матрицю системи до трикутного вигляду за модифікованим методом Гауса:

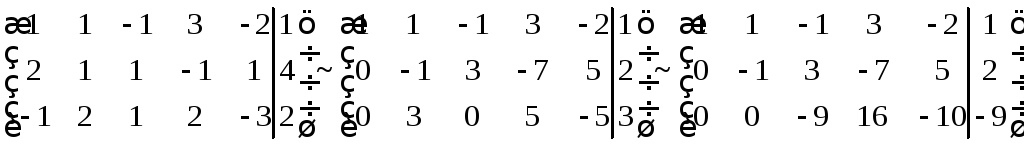
Обернений хід  випишемо відповідну останній розширеній матриці систему рівнянь:

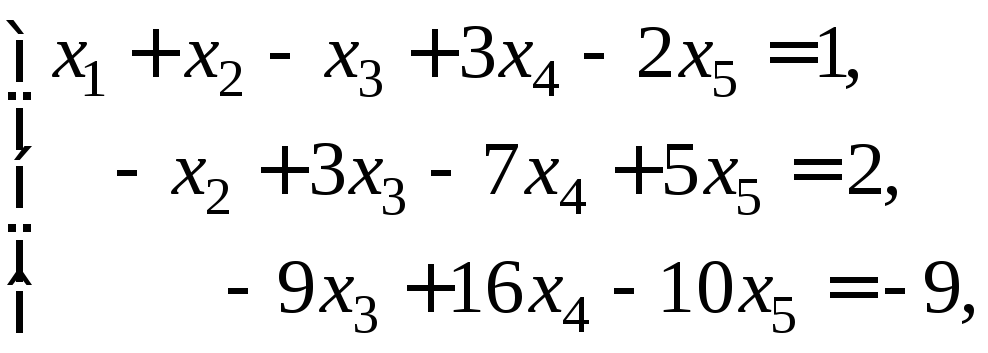
З останньої рівності знайдемо: , який підставимо у друге рівняння і одержимо:. В перше рівняння підставляємо вирази дляічерезіі одержимо.

Отже, загальний розв’язок системи має вигляд:

.

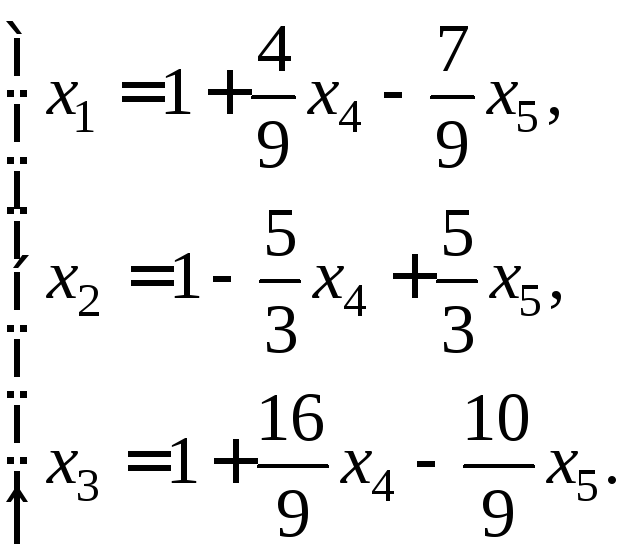Тут  вільні змінні;  основні змінні.

Надамо вільним змінним певних значень і випишемо частинні розв’язки:

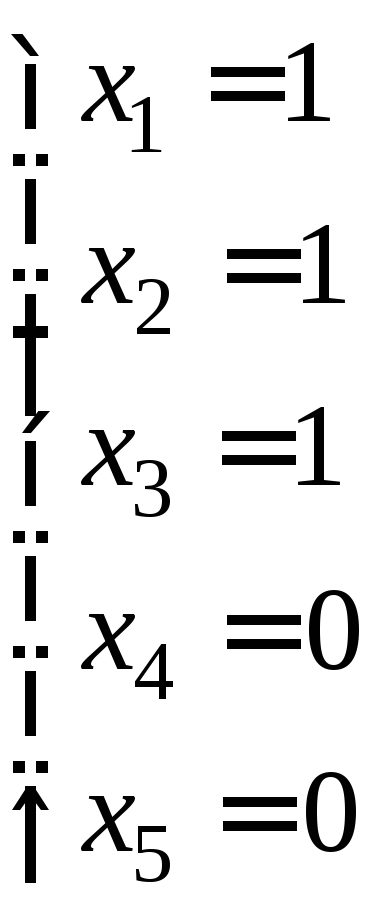
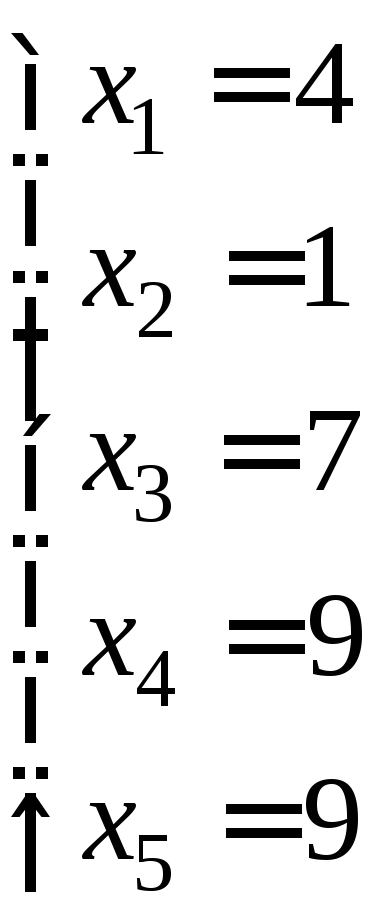
Зауваження.

Якщо після виконання алгоритму прямого ходу система містить рівняння , де, тоді система не сумісна.

Зауваження.

Якщо для квадратної системи лінійних рівнянь за методом Крамера зроблено висновок про безліч рішень, тоді за прямим ходом метода Гаусса з’явиться нульовий рядок, на який не зважають.

2. Елементи аналітичної геометрії

2.1. Векторна алгебра

Найчастіше ми звикли використовувати скалярні величини (або скаляри), тобто такі величини для характеристики яких достатньо задати їх числове значення. Скалярними величинами є температура, маса, час, густина, площа, об’єм, довжина відрізка, електричний заряд, опір провідника, прибуток, рентабельність, обсяг виробництва, витрати підприємства, товарообіг.

Величини, які крім абсолютної величини характеризуються ще й напрямком, називають векторними. Вектори часто використовують у математиці, фізиці і технічних науках. Наприклад, силу характеризують дві властивості – модуль і напрямок. Сила є прикладом векторної величини. Багато інших фізичних величин (момент сили, швидкість, прискорення, напруженість силового поля) також є векторними величинами.

Векторна величина геометрично зображається з допомогою направленого відрізка певної довжини і певному масштабі після вибору одиниці масштабу.

Вектором називають направлений відрізок прямої (або упорядковану пару точок).

Вектор позначається двома буквами, причому перша  початок вектора, друга  його кінець. Наприклад,  вектор, початок якого збігається з точкою , а кінець з точкою , напрямок – віддо. Часто вектор позначають однією буквою, наприклад. Якщо вектор позначений однією буквою, то часто в книгах її виділяють жирним шрифтом, але без риски.

Геометрично вектор зображують відрізком із стрілкою (рис.2.1).

Рисунок 2.1  Вектор

Довжиною (або модулем) вектора називають довжину відрізку, який його породжує.

Одиничним вектором (або ортом) називають вектор, довжина якого дорівнює одиниці.

Очевидно, що коли дано довільний вектор , то поділивши його на його довжину, одержимо одиничний вектор, наприклад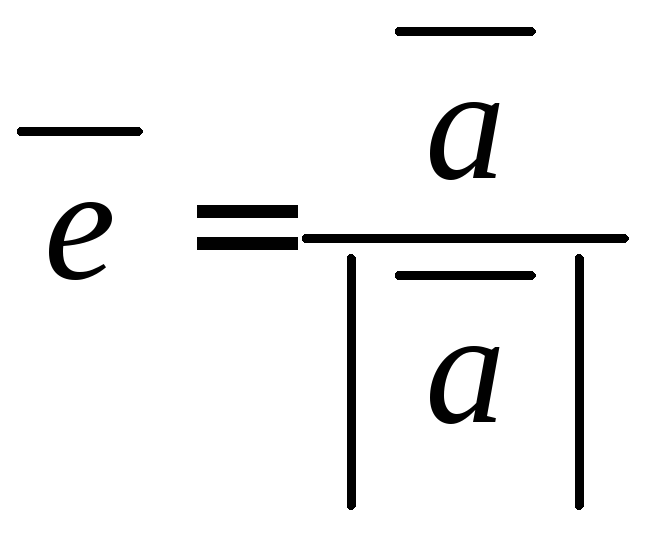, напрямок якого збігається з напрямком вектора.

Два вектори іназивають колінеарними , якщо вони лежать на паралельних прямих (рис. 2.2).

Рисунок 2.2  Колінеарні вектори.

Нульовий вектор є колінеарним з будь-яким вектором.

Два вектори іназивають рівними , якщо вони колінеарні і мають однакові довжину і напрямок (рис.2.3).

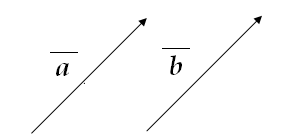
Рисунок 2.3  Рівні вектори .

Два вектори іназивають взаємно протилежними , якщо вони колінеарні, мають однакову довжину і протилежно направлені (рис. 2.4).

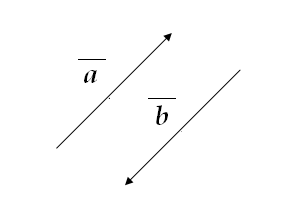
Рисунок 2.4  Взаємно протилежні вектори .

Позначають протилежний до вектору вектор як.

Вектори називають компланарними, якщо вони лежать в одній площині або паралельні їй.

Колінеарні вектори завжди компланарні, однак не всі компланарні вектори є колінеарними.

Два вектори іназивають ортогональними , якщо вони лежать на перпендикулярних прямих.

З означення вектору випливає наступне: при паралельному перенесенні вектору одержимо вектор, що дорівнює початковому. Тому початок вектору можна розміщувати у будь-якій точці простору. Отже, вектор може починатися в будь-якій точці простору. Домовимося вважати, що початок вектора співпадає з початком координат.

Над векторами як математичними об’єктами можна виконувати певні дії.