Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Донецкий национальный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Met_VM_1_3.doc

Скачиваний:

582

Добавлен:

03.03.2016

Размер:

5.81 Mб

Скачать

☆

<<< < Предыдущая 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 1920 / 2720 21 22 23 24 25 26 27 > Следующая >>>

Основні еквівалентності при

Приклад 4.21.

Довести, що функції іприє нескінченно малими одного порядку.

Розв’язання. Знайдемо границю відношення заданих функцій:

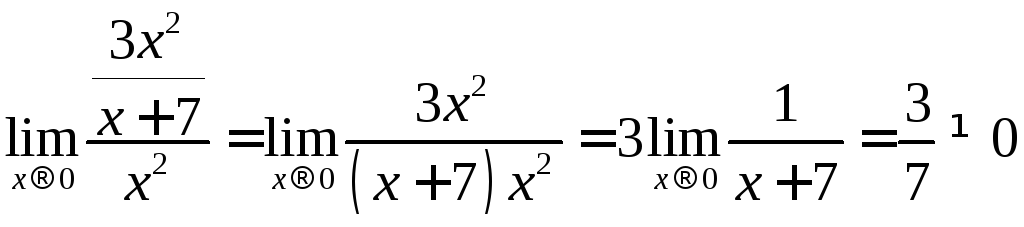Таким чином, дані функції є нескінченно малими одного порядку.

Приклад 4.22.

Чи є еквівалентними функції іпри?

Розв’язання. Знайдемо границю відношення цих функцій:

Таким чином, функція є нескінченно малою вищого порядку, ніж функція тобто дані функції не є еквівалентними.

Приклад 4.23.

Довести, що нескінченно малі функції іприє еквівалентними.

Розв’язання. Очевидно, що 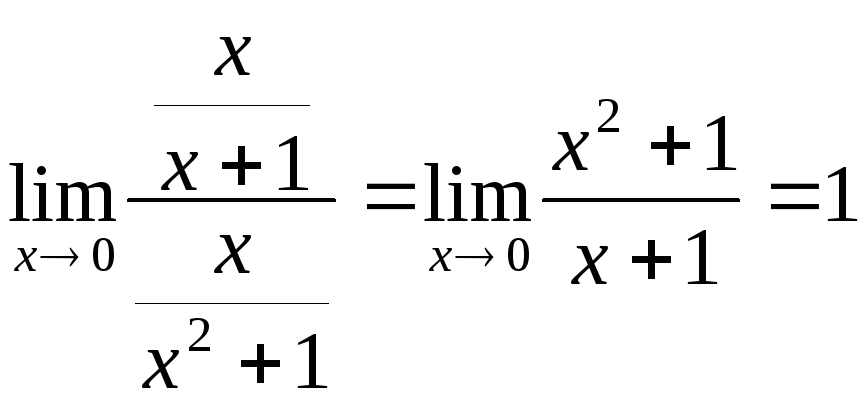. Отже,іприx  0 є еквівалентними.

Приклад 4.24.

Знайти .

Розв’язання. При функціяє нескінченно малою. Оскільки при заміні нескінченно малої функціїеквівалентною їй функцієюза теоремою 4.1. границя відношення не зміниться, то

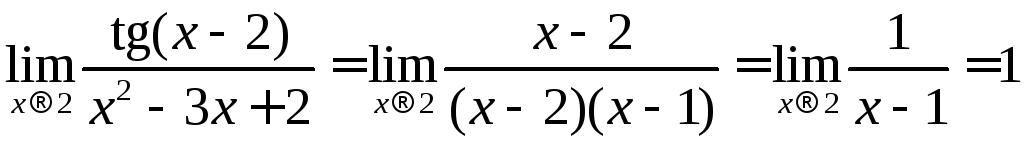Приклад 4.24.

Знайти .

Розв’язання. Оскільки при x0 ,а і оскільки за теоремою 4.1 границя відношення не зміниться, то

Приклад 4.25.

Знайти .

Розв’язання. Тут чисельник і знаменник – нескінченно малі функції, проте, х не є нескінченно малою функцією, оскільки , а не до нуля. Введемо нескінченно малу, тоді. Маємо

5. Неперервність функції

5.1. Неперервність функції в точці і на відрізку

Функцію , що визначена в деякому околі точки, називаютьнеперервною в точці , якщо:

вона визначена в точці , тобто існує ;
існує границя функції при , що прямує до , тобто існує ;
ця границя дорівнює значенню функції в точці х₀, тобто

Наведемо означення неперервності функції, яке є еквівалентним попередньому, і засноване на понятті нескінченно малої величини. Дамо аргументу приріст , тоді функціяотримає приріст.

Функцію називаютьнеперервною в точці , якщо вона визначена в цій точці і нескінченно малому приросту аргументу відповідає нескінченно малий приріст функції, тобто

Зауваження.

Визначення неперервності функції в точці може бути записане так:

тобто для неперервної функції можлива перестановка символів границі і функції.

Зауваження.

Друга умова неперервності функції означає зокрема, що

Властивості функцій, які неперервні в точці

1)	Якщо функції інеперервнів точці , то їх сума , добутокі часткає функціями, неперервнимив точці .
2)	Якщо функція неперервнав точці і , тоіснує такий окіл точки , в якому .
3)	Якщо функція неперервнав точці , а функціянеперервнав точці , то складна функціянеперервнав точці .