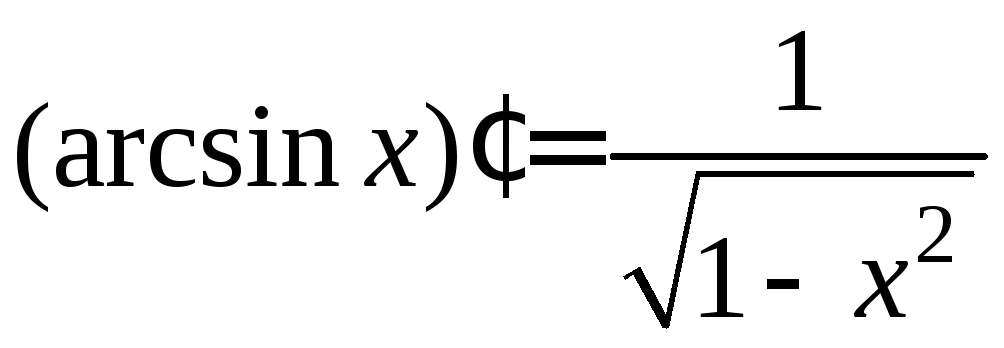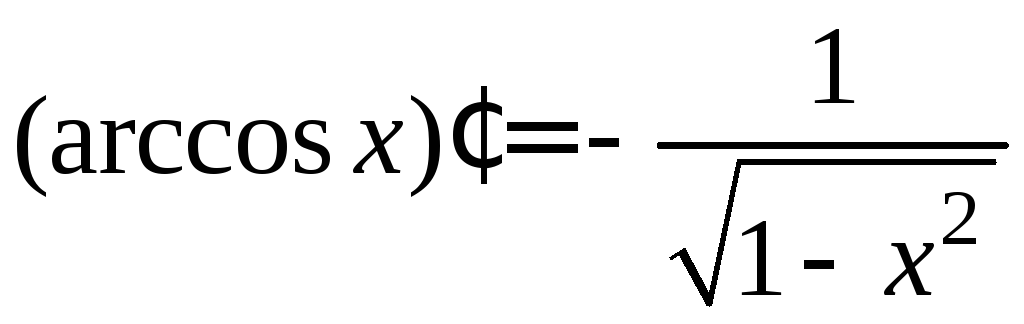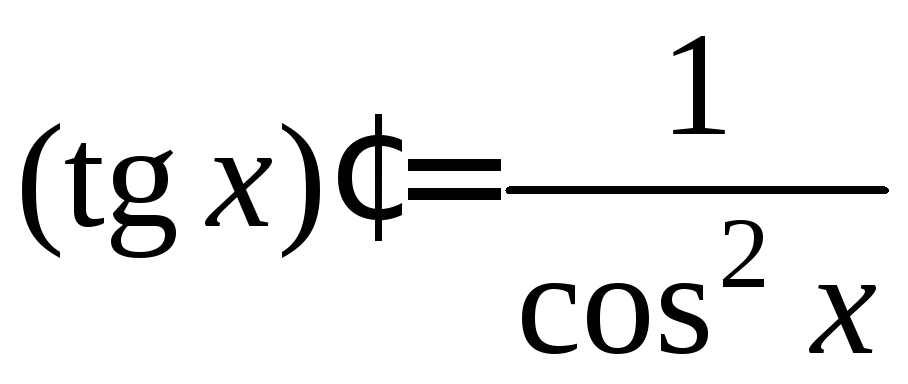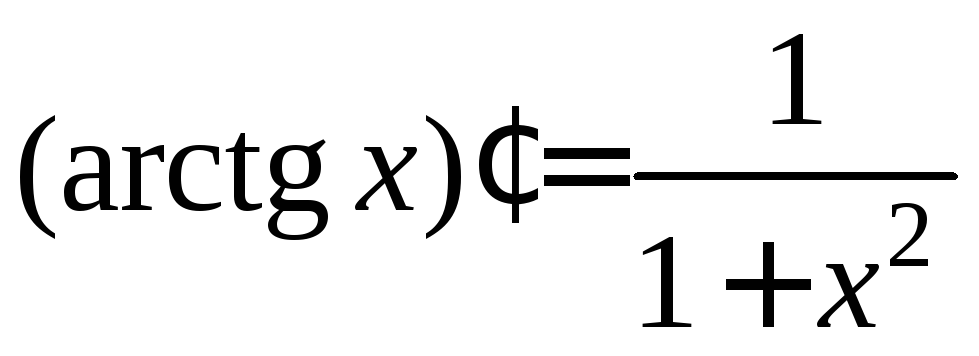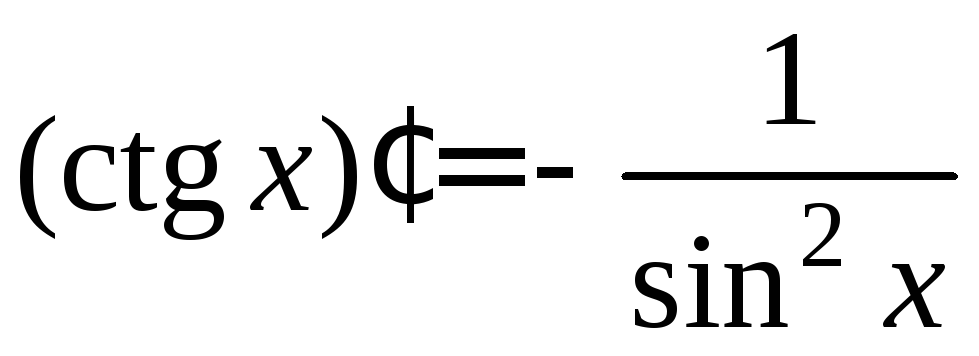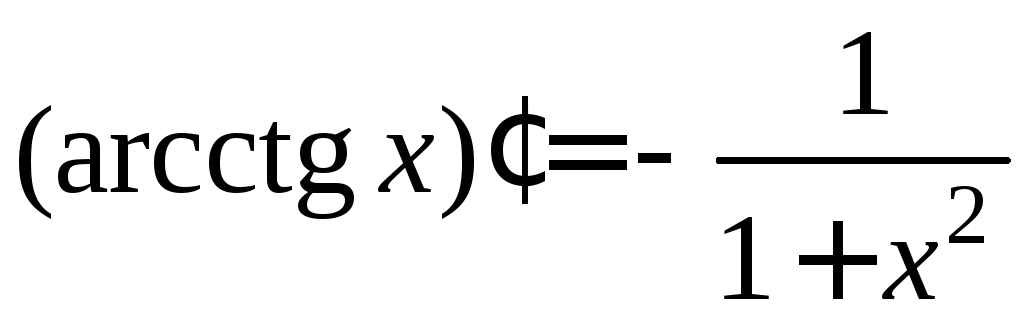- •Міністерство освіти і науки,
- •Правила оформлення контрольної роботи
- •1. Елементи лінійної алгебри
- •1.1. Матриці та дії над ними
- •Дії над матрицями
- •Основні властивості множення матриці на число
- •Основні властивості додавання та віднімання матриць
- •Основні властивості множення матриць
- •Основні властивості транспонування матриці
- •1.2. Визначники та способи їх обчислення
- •Основні властивості визначників
- •Алгоритм обчислення оберненої матриці
- •Властивості обертання невироджених матриць
- •1.3. Системи лінійних рівнянь
- •Елементарні перетворення системи лінійних рівнянь
- •Метод Крамера
- •Метод оберненої матриці
- •Метод Гаусса
- •Алгоритм прямого ходу методу Гаусса
- •2. Елементи аналітичної геометрії
- •2.1. Векторна алгебра
- •Дії над векторами
- •Властивості лінійних операцій над векторами
- •Основні властивості проекцій
- •Дії над векторами в координатній формі
- •Скалярний добуток векторів
- •Основні властивості скалярного добутку векторів
- •Векторний добуток векторів
- •Основні властивості векторного добутку векторів
- •Мішаний добуток векторів
- •Основні властивості мішаного добутку векторів
- •2.2. Пряма на площині
- •Умови взаємного розташування на площині точок і прямих
- •Контрольні питання зі змістового модуля I
- •3. Границя числової послідовності та функції. ОСновні пОняття
- •3.1. Функціональна залежність. Огляд основних елементарних функцій
- •3.2. Границя послідовності та її властивості
- •Основні теореми про послідовності, що збігаються
- •3.3. Нескінченно малі та нескінченно великі послідовності
- •Властивості нескінченно малих послідовностей
- •Властивості нескінченно великих послідовностей
- •Зв’язок між нескінченно великими і нескінченно малими послідовностями
- •3.4. Границя функції та її властивості
- •Односторонні границі функції
- •4. Обчислення границь
- •4.1. Методи розкриття невизначеностей
- •4.2. Визначні границі
- •4.3. Порівняння нескінченно малих функцій
- •Основні еквівалентності при
- •5. Неперервність функції
- •5.1. Неперервність функції в точці і на відрізку
- •Властивості функцій, які неперервні в точці
- •Властивості функцій, що неперервні на відрізку
- •5.2. Класифікація точок розриву
- •Контрольні питання зі змістового модуля II
- •6. Похідна функції однієї змінної
- •6.1. Диференційованість функції однієї змінної. Правила обчислення похідних
- •Правило знаходження похідної
- •Основні властивості похідної
- •6.2. Таблиця похідних основних елементарних функцій. Похідні вищих порядків
- •3 (Куб), ,,,.
- •6.3. Похідні функцій, заданих у параметричній, неявній формах, логарифмічне диференціювання
- •6.4. Диференціал функції однієї змінної
- •7. Диференційованість функції багатьох змінних
- •7.1. Частинні похідні та повний диференціал
- •Повний диференціал першого порядку
- •7.2. Похідна неявної, складної функції. Похідна за напрямом
- •Контрольні питання зі змістового модуля III
Правило знаходження похідної
|
1) |
надамо
значенню
|
|
2) |
обчислимо
приріст функції
|
|
3) |
складемо
відношення
|
|
4) |
знайдемо
границю цього відношення при
|
|
Приклад 6.1. |
Знайти
похідну функції
|
Розв’язання.
За допомогою правила знаходження
похідної аргументу
![]() надамо приросту
надамо приросту![]() ,
тоді приріст досліджуваної функції
,
тоді приріст досліджуваної функції![]() складе
складе
![]() .
.
Відношення приросту функції до приросту аргументу має вигляд:
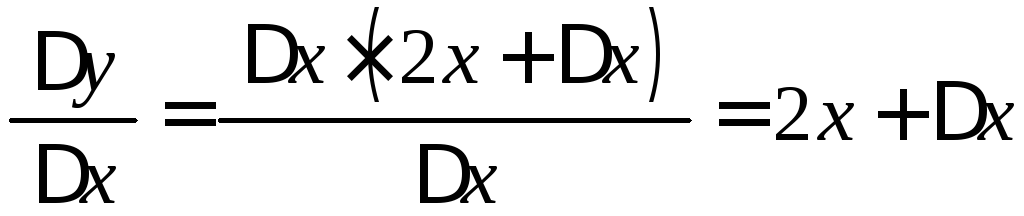 .
.
Границя
цього відношення при
![]() і становить похідну функції:
і становить похідну функції:
![]() .
.
|
Теорема 6.1. |
(зв’язок
між диференційованістю та неперервністю
функції)
Якщо
функція
|
|
Зауваження.
|
З
неперервності функції не впливає її
диференційованість.
Наприклад, функція
|
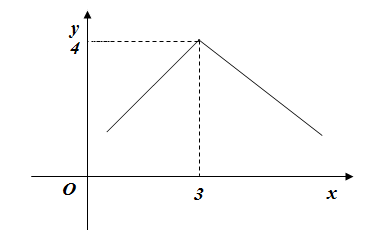
Рисунок 6.5 – Графік неперервної недиференційованої функції.
Основні властивості похідної
|
1) |
Сталий множник можна винести за знак похідної:
|
|
2) |
Похідна від алгебраїчної суми двох диференційованих функцій дорівнює алгебраїчній сумі похідній цих функцій:
|
|
3) |
Похідну добутку двох диференційованих функцій обчислюють за формулою:
|
|
4) |
Похідна частки двох диференційованих функцій дорівнює
якщо
|
|
5) |
Похідна складної функції: Нехай
|
|
6) |
Похідна оберненої функції: Нехай
для диференційованої функції
|
6.2. Таблиця похідних основних елементарних функцій. Похідні вищих порядків
Таблиця похідних основних елементарних функцій:
|
1)
|
5)
|
9)
|
|
2)
|
6)
|
10)
|
|
3)
|
7)
|
11)
|
|
4)
|
8)
|
12)
|
Нехай
функція
![]() диференційована на деякому проміжку.
Похідну
диференційована на деякому проміжку.
Похідну![]() називаютьпохідною
першого порядку
або першою
похідною функції
називаютьпохідною
першого порядку
або першою
похідною функції
![]() .
Якщо перша похідна
.
Якщо перша похідна![]() є диференційованою функцією на проміжку,
то її похідну називаютьдругою
похідною або
похідною
другого порядку
функції
є диференційованою функцією на проміжку,
то її похідну називаютьдругою
похідною або
похідною
другого порядку
функції
![]() і позначають
і позначають![]() .
.
Аналогічно вводять поняття похідної п-го порядку:
![]() ,
,
де
![]() – натуральне число.
– натуральне число.
Отже,
похідна від похідної – це похідна
другого порядку
![]() .
Похідну третього порядку позначають
таким чином:
.
Похідну третього порядку позначають
таким чином:![]() і т.д.
і т.д.
Похідні порядку вище першого називають похідними вищих порядків.
Якщо
![]() – закон прямолінійного руху матеріальної
точки, то
– закон прямолінійного руху матеріальної
точки, то![]() ‑ це прискорення цієї точки в момент
часу
‑ це прискорення цієї точки в момент
часу![]() .
В цьому полягає фізичний зміст другої
похідної.
.
В цьому полягає фізичний зміст другої
похідної.
|
Приклад 6.2. |
Знайти
похідну функції
|
Розв’язання.
Диференціюємо
спочатку тангенс, враховуючи, що роль
проміжного аргументу виконує
![]() .
Одержимо
.
Одержимо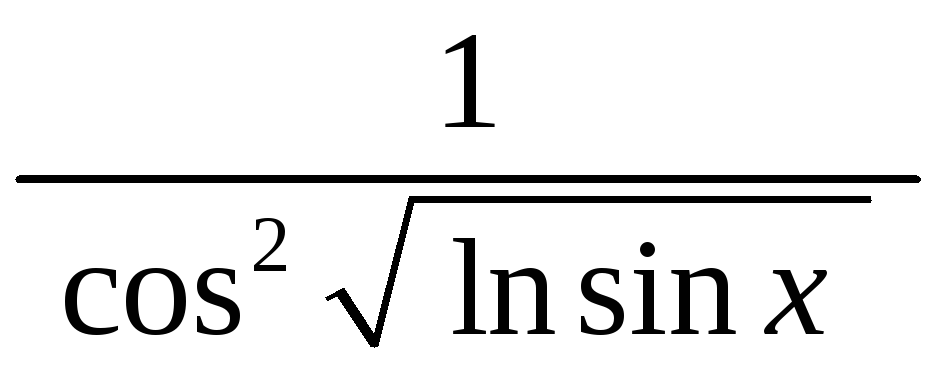 .
Тепер подумки закреслимо значок «
.
Тепер подумки закреслимо значок «![]() »
і бачимо перед собою вираз
»
і бачимо перед собою вираз![]() .
Диференціюємо корінь:
.
Диференціюємо корінь: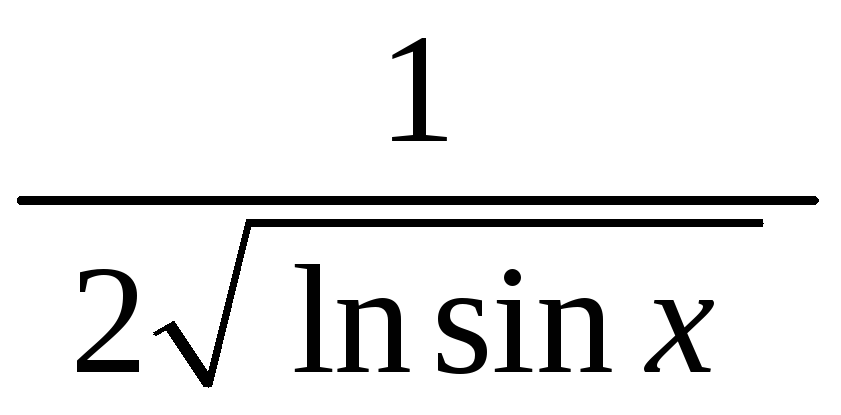 і
потім подумки закриваємо значок кореня.
Залишається
і
потім подумки закриваємо значок кореня.
Залишається![]() .
Диференційований логарифм (проміжним
аргументом є
.
Диференційований логарифм (проміжним
аргументом є![]() ):
):![]() .
Після викреслювання значка «
.
Після викреслювання значка «![]() »
залишається
»
залишається![]() ,
що при диференціюванні дає
,
що при диференціюванні дає![]() .
Тепер похідна
.
Тепер похідна![]() запишеться у вигляді добутку всіх
проміжних результатів диференціювання:
запишеться у вигляді добутку всіх
проміжних результатів диференціювання:
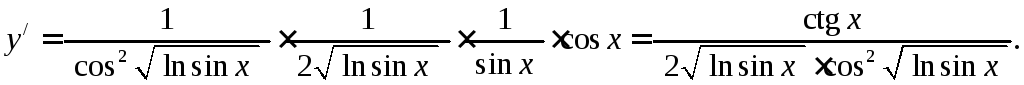
|
Приклад 6.3. |
Знайти
похідну функції
|
Розв’язання. Порядок уявного закреслювання наступний:

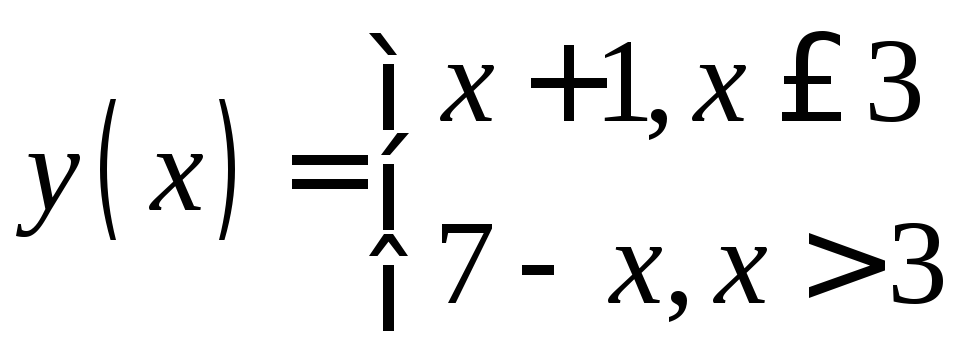 є неперервною, але не диференційованою
(рис. 6.5).
є неперервною, але не диференційованою
(рис. 6.5). ,
,
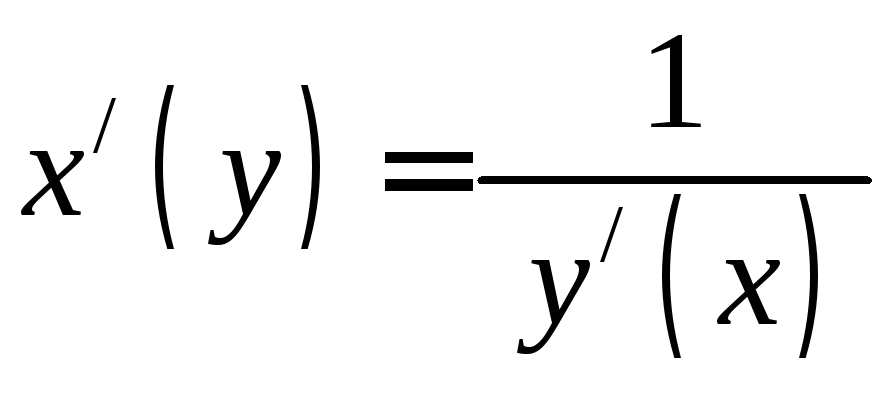 .
.