4.2. Визначні границі

При обчисленні границь тригонометричних виразів часто використовують формулу:

. (4.1)

Формулу (4.1) називають першою визначною границею і застосовують для розкриття невизначеностей вигляду у разі коли функція, що стоїть під знаком границі, містить тригонометричні функції.

Справедливі наступні співвідношення:

, ,. (4.2)

Приклад 4.12.

Знайти .

Розв’язання. При х0 вираз також прямує до нуля, тому, помноживши чисельник і знаменник на 7, отримаємо:

.

Приклад 4.13.

Знайти .

Розв’язання. При х0 маємо невизначеність . Тому, враховуючи, що, та помножуючи чисельник і знаменник на 25х, отримаємо:

.

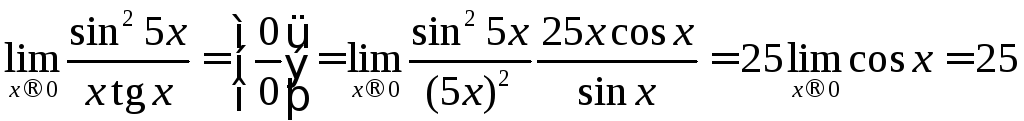Приклад 4.14.

Знайти .

Розв’язання. При х0 маємо невизначеність вигляду , тому, вводячи нову зміннуу, отримаємо

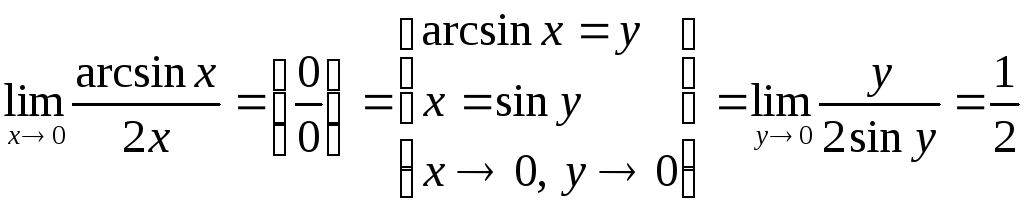
Приклад 4.15.

Знайти .

Розв’язання. 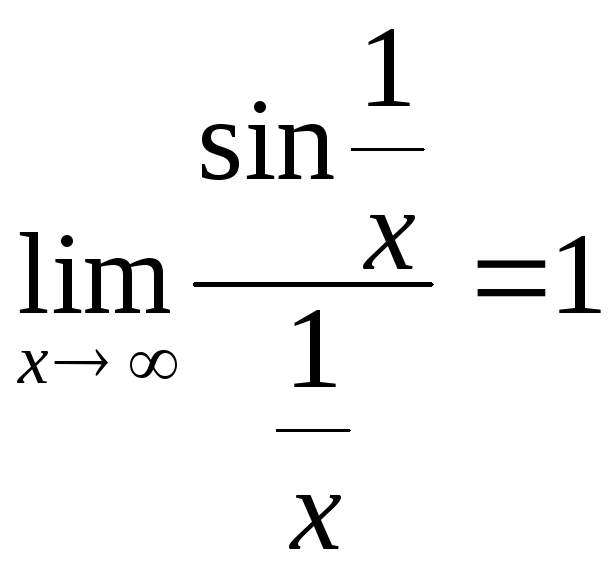за формулою (4.1), оскільки при.

Границею функції приназивають числоe. Воно ірраціональне. Приблизне значення . Маємо:

. (4.3)

Позначення цієї границі через e прийняте на знак пошани до Ейлера. Число e має велике значення в математичному аналізі і його застосуваннях. Співвідношення (4.3) називають другою визначною границею. Співвідношення (4.3) можна записати у вигляді:

. (4.4)

Другу визначну границю застосовують при розкритті невизначеності .

Приклад 4.16.

Знайти .

Розв’язання. При хмаємо невизначеність тому, перетворюючи вираз, що стоїть під знаком границі до вигляду (4.3), отримаємо:

.

Приклад 4.17.

Знайти .

Розв’язання. При хмаємо невизначеність тому, виділивши цілу частину в функції, що стоїть під знаком границі, за допомогою (4.4) отримаємо:

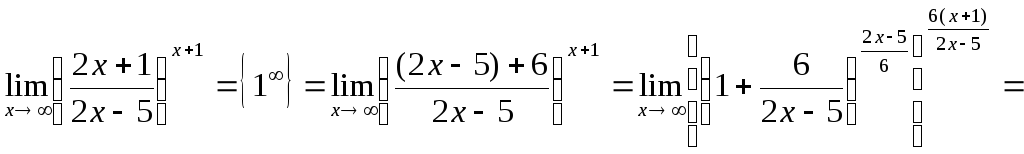
Приклад 4.18.

Знайти .

Розв’язання. Спочатку перетворимо вираз, що стоїть під знаком границі, використовуючи властивості логарифмів, а потім скористаємось (4.4):

.

Приклад 4.19.

Знайти .

Розв’язання. Виконавши перетворення з використанням властивостей логарифмів, за допомогою (4.3) отримаємо:

.

Приклад 4.20.

Знайти .

Розв’язання. Перейшовши до нової змінної, за допомогою (4.3) отримаємо:

.

4.3. Порівняння нескінченно малих функцій

Нехай і– нескінченно малі функції при, причомуможе бути як числом, так одним з символів . Тоді справедливі наступні означення.

Якщо , то функціюназиваютьнескінченно малою функцією вищого порядку мализни в порівнянні з функцією , а функціюназиваютьнескінченно малою функцією нижчого порядку мализни в порівнянні з функцією .

Якщо , то функціюназиваютьнескінченно малою функцією нижчого порядку мализни в порівнянні з функцією , а функцію називаютьнескінченно малою функцією вищого порядку мализни в порівнянні з функцією .

Якщо і,, то функціїтаназиваютьфункціями одного порядку мализни.

Якщо , то нескінченно малі функціїіназиваютьеквівалентними. Позначення: .

Якщо і,, то функціюназиваютьнескінченно малою функцією -го порядку мализни відносно нескінченно малої функції .

Теорема 4.1.

Границя відношення двох нескінченно малих функцій не зміниться, якщо кожну з них або яку-небудь одну замінити еквівалентними ним.

При обчисленні границь функцій зручно користуватися теоремою 17 і наступними основними еквівалентностями.