Контрольні питання зі змістового модуля II

3.1.	Дати означення функції, її області визначення та значень
3.2.	Яка функція називається парною, непарною, періодичною?
3.3.	Які функції називають монотонними?
3.4.	Назвати основні елементарні функції.
3.5.	Дати означення числової послідовності та її границі.
3.6.	Сформулювати основні теореми про послідовності, що збігаються.
3.7.	Дати означення нескінченно малої числової послідовності, навести приклади. Сформулювати властивості нескінченно малих послідовностей.
3.8.	Дати означення нескінченно великої числової послідовності, навести приклади. Сформулювати властивості нескінченно великих послідовностей та їх зв’язок з нескінченно малими послідовностями.
3.9.	Дати означення границі функції за Коші та за Гейне. Чи є вони еквівалентними?
3.10.	Дати означення границь функції на нескінченності та нескінченних границь, а також односторонніх границь.
4.1.	Що таке невизначеність. Навести приклади.
4.2.	Назвати основні методи розкриття невизначеностей раціональних функцій.
4.3.	Назвати основні методи розкриття невизначеностей тригонометричних функцій. Що таке перша визначна границя?
4.4.	Що таке друга визначна границя? Для яких невизначеностей її застосовують?
4.5.	Дати означення функцій вищого порядку мализни, нижчого порядку, одного порядку мализни, еквівалентних функцій.
4.6.	Навести основні еквівалентності для нескінченно малого аргументу.
5.1.	Дати означення функції, неперервної в точці та на відрізку. Навести властивості функцій, неперервних в точці та властивості функцій, неперервних на відрізку.
5.2.	Що можна сказати про неперервність елементарних функцій?
5.3.	Дати визначення точки розриву.
5.4.	Назвати типи точок розриву. Навести приклади
	.

ЗМІСТОВИЙ МОДУЛЬ 3

ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЙ

ОДНІЄЇ ТА БАГАТЬОХ ЗМІННИХ

6. Похідна функції однієї змінної

6.1. Диференційованість функції однієї змінної. Правила обчислення похідних

Спочатку розглянемо поняття дотичної. Відоме зі шкільного курсу, воно носить формальний характер і не дозволяє побудувати дотичну в загальному випадку. Дамо інше визначення дотичної.

Виберемо на кривій точкуі проведемо в ній будь-яку січну(рис. 6.1). Якщо точкупересувати вздовж кривої до точки, то січнабуде займати положення,і т.д.

Рисунок 6.1 – Ілюстрація к поняттю дотичної

Припустимо, що при необмеженому наближенні точки до точкисічнанамагається зайняти певне положення. В цьому випадку прямуназивають дотичною до кривоїв точці.

Звернемо увагу на те, що точку ми вибираємо довільно, тобто з будь-якого боку від точки, але граничне положення січноїповинне бути тим самим (рис. 6.2). Якщо залежно від вибору точкисічнапрагне зайняти різні положення, то дотичної у точціне існує (або говорять, що існує правобічна та лівобічна дотичні) (рис. 6.3).

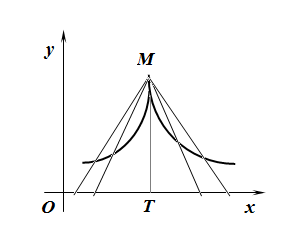
Рисунок 6.2 – Вертикальна дотична

Рисунок 6.3 – Відсутність дотичної в точці

На рис. 6.2 дотичною до кривої в точці є пряма, на рис. 6.3 дотичної у точціне існує (існує лівобічна дотичнаі правобічна дотична; дотична в точцііснувала б у тому випадку, якбизбіглася б з).

Дамо означення поняттю похідної.

Нехай – деяка функція, задана на інтервалі. На кривій, що визначається рівняннямвізьмемо довільну точкуз абсцисоюз інтервалу. Значення функції в цій точці буде. Надамо аргументу приростутаким чином, щоб точкатеж належала інтервалу. Новому значеннювідповідає точкакривої. Значенням функції в новій точці буде.

Рисунок 6.4 – Ілюстрація поняття похідної

Приріст функції складе (рис. 6.4) . Побудуємо відношення, яке показує, у скільки разів «у середньому» прирістфункції більше (або менше) приростуїї аргументу. Це відношення називають середньою швидкістю зміни функціїна ділянці. Чим менше значення, тим краще середня швидкість на ділянцібуде характеризувати ту швидкість, з якої міняється функція в точці. Тому за швидкість зміни функції в точціприродньо прийняти границю

.

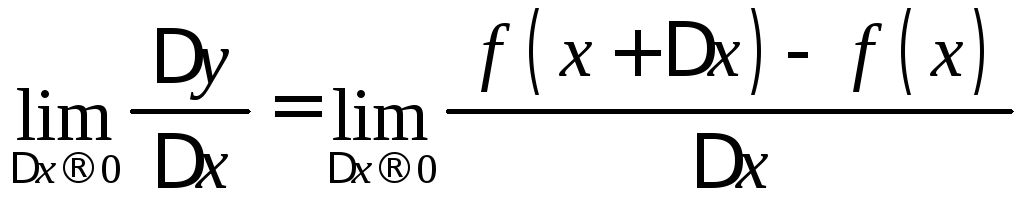Ця границя і називається похідною.

Якщо існує скінченна границя відношення при, то цю границю називаютьпохідною функції в точці і позначають . (6.1)

Означення похідної можна подати й у такому вигляді.

Похідною функції називають границю відношення приростуфункції до нескінченно малого приросту аргументу, який його викликав.

Знаходження похідної функції називають її диференціюванням. Якщо функція має похідну в точці, то кажуть, що функціядиференційована в точці . Якщо функціядиференційована в кожній точці інтервалу, то вона єдиференційованою на інтервалі .

Похідна представляє собою швидкість зміни функції в точці , тобто швидкість, з якою змінюється функція при переході через точку. Такий найбільш загальний зміст похідної.

Поняття похідної дозволяє характеризувати локальну поведінку функції і ввести апарат дослідження функцій.

Розглянемо на площині криву, задану рівнянням(рис. 64). Візьмемо точкиіна кривій. Пряманазивається січною. Вона утворює з додатним напрямком осікут. Кутовий коефіцієнт січної дорівнює тангенсу. З розгляду трикутникамаємо.

Почнемо рухати точку вздовж кривоїдо точки. При цьому точканескінченно наближується до точки, а січназмінює своє положення, аж доки не займе положення дотичної. Прямаутворює з віссюкут, тому її кутовий коефіцієнт дорівнює.

При нескінченному наближенні точки до точкисічнанескінченно наближується до дотичної. Отже, при цьомуабо, враховуючи неперервність тангенса(очевидно, що умовуможна замінити)

.

Таким чином, кутовий коефіцієнт невертикальної дотичної до графіка функції в точцідорівнює значенню похідної в точці:. У цьому полягаєгеометричний зміст похідної.

Механічний зміст похідної: похідна функції в точцівизначає швидкість зміни функції в цій точці.

У теоретичному плані підкреслимо, що існування границі, якою виражається похідна, треба розуміти в загальному значенні існування границі функції в точці. Це означає, що повинна існувати не тільки при, але й при, причому обидві границі повинні збігатися. У цій вимозі й полягає умова існування похідної у точці.

З геометричної точки зору ця умова означає незалежність граничного положення січної від того, чи вибирали ми точку праворуч або ліворуч від точки, на що було зазначено раніше.