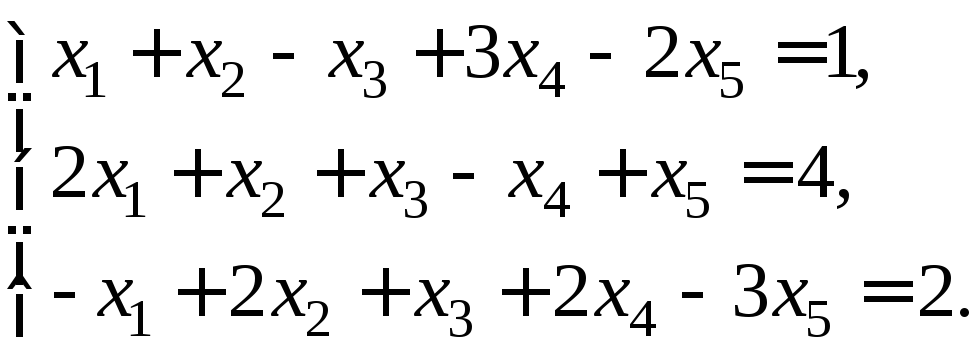- •Міністерство освіти і науки,
- •Правила оформлення контрольної роботи
- •1. Елементи лінійної алгебри
- •1.1. Матриці та дії над ними
- •Дії над матрицями
- •Основні властивості множення матриці на число
- •Основні властивості додавання та віднімання матриць
- •Основні властивості множення матриць
- •Основні властивості транспонування матриці
- •1.2. Визначники та способи їх обчислення
- •Основні властивості визначників
- •Алгоритм обчислення оберненої матриці
- •Властивості обертання невироджених матриць
- •1.3. Системи лінійних рівнянь
- •Елементарні перетворення системи лінійних рівнянь
- •Метод Крамера
- •Метод оберненої матриці
- •Метод Гаусса
- •Алгоритм прямого ходу методу Гаусса
- •2. Елементи аналітичної геометрії
- •2.1. Векторна алгебра
- •Дії над векторами
- •Властивості лінійних операцій над векторами
- •Основні властивості проекцій
- •Дії над векторами в координатній формі
- •Скалярний добуток векторів
- •Основні властивості скалярного добутку векторів
- •Векторний добуток векторів
- •Основні властивості векторного добутку векторів
- •Мішаний добуток векторів
- •Основні властивості мішаного добутку векторів
- •2.2. Пряма на площині
- •Умови взаємного розташування на площині точок і прямих
- •Контрольні питання зі змістового модуля I
- •3. Границя числової послідовності та функції. ОСновні пОняття
- •3.1. Функціональна залежність. Огляд основних елементарних функцій
- •3.2. Границя послідовності та її властивості
- •Основні теореми про послідовності, що збігаються
- •3.3. Нескінченно малі та нескінченно великі послідовності
- •Властивості нескінченно малих послідовностей
- •Властивості нескінченно великих послідовностей
- •Зв’язок між нескінченно великими і нескінченно малими послідовностями
- •3.4. Границя функції та її властивості
- •Односторонні границі функції
- •4. Обчислення границь
- •4.1. Методи розкриття невизначеностей
- •4.2. Визначні границі
- •4.3. Порівняння нескінченно малих функцій
- •Основні еквівалентності при
- •5. Неперервність функції
- •5.1. Неперервність функції в точці і на відрізку
- •Властивості функцій, які неперервні в точці
- •Властивості функцій, що неперервні на відрізку
- •5.2. Класифікація точок розриву
- •Контрольні питання зі змістового модуля II
- •6. Похідна функції однієї змінної
- •6.1. Диференційованість функції однієї змінної. Правила обчислення похідних
- •Правило знаходження похідної
- •Основні властивості похідної
- •6.2. Таблиця похідних основних елементарних функцій. Похідні вищих порядків
- •3 (Куб), ,,,.
- •6.3. Похідні функцій, заданих у параметричній, неявній формах, логарифмічне диференціювання
- •6.4. Диференціал функції однієї змінної
- •7. Диференційованість функції багатьох змінних
- •7.1. Частинні похідні та повний диференціал
- •Повний диференціал першого порядку
- •7.2. Похідна неявної, складної функції. Похідна за напрямом
- •Контрольні питання зі змістового модуля III
Властивості обертання невироджених матриць
|
1) |
|
|
2) |
|
|
3) |
|
|
4) |
|
|
5) |
|
|
Приклад 1.4. |
Знайти
обернену до матриці
|
Розв’язання.
Визначник
матриці
![]() відрізняється від нуля:
відрізняється від нуля:
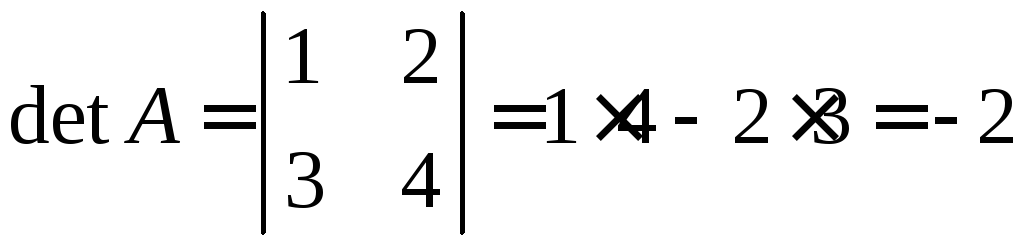 .
.
Отже
матриця
![]() є невиродженою і обернена до неї
є невиродженою і обернена до неї![]() існує.
Знайдемо алгебраїчні доповнення до
кожного елементу вихідної матриці:
існує.
Знайдемо алгебраїчні доповнення до
кожного елементу вихідної матриці:
![]() ,
,
![]() ,
,![]() ,
,![]() .
.
За
формулою (1.6) можемо записати:
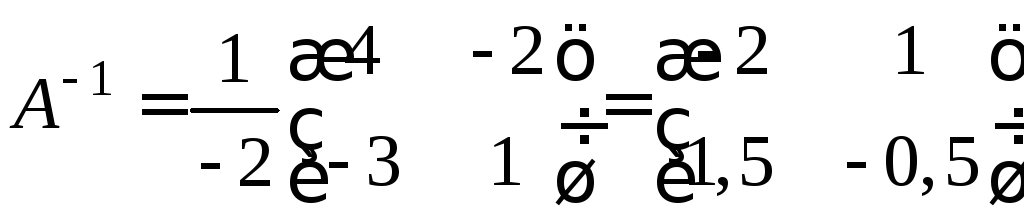 .
.
Перевірка підтверджує правильність проведених обчислень:
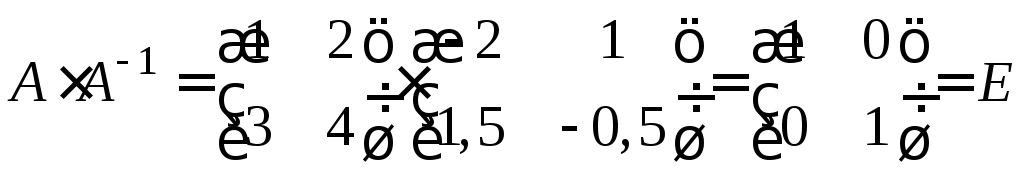 ,
,

|
Приклад 1.5. |
Знайти
обернену до матриці
|
Розв’язання.
Вихідна матриця
![]() є не виродженою, оскільки
є не виродженою, оскільки![]() .
Обчислимо алгебраїчні доповнення:
.
Обчислимо алгебраїчні доповнення:
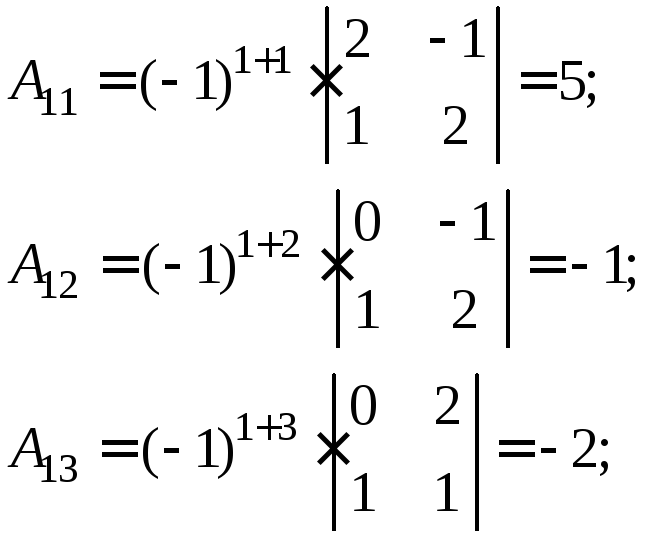


За формулою (1.7) маємо:
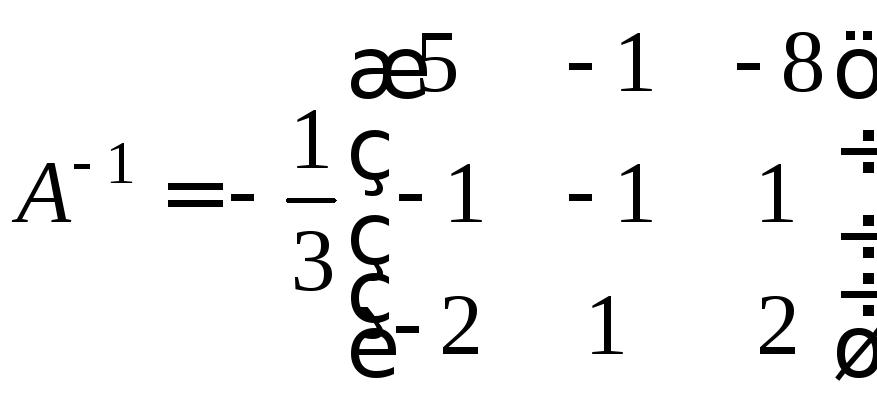 ,
отже
,
отже
 .
.
|
|
Рангом
матриці
|
Ранг
матриці визначається порядком ненульового
мінору, а не його значенням. Якщо
![]() ,
то це означає, що існує хоча б один
відмінний від нуля мінор порядку
,
то це означає, що існує хоча б один
відмінний від нуля мінор порядку![]() ,
а всі мінори порядку, більшого від
,
а всі мінори порядку, більшого від![]() дорівнюють
нулю. Зрозуміло, що
дорівнюють
нулю. Зрозуміло, що
![]() .
.
1.3. Системи лінійних рівнянь
|
|
Системою
лінійних алгебраїчних рівнянь
називають сукупність
де
|
|
|
Якщо
всі вільні члени дорівнюють нулю
|
Випишемо
основну матрицю системи:
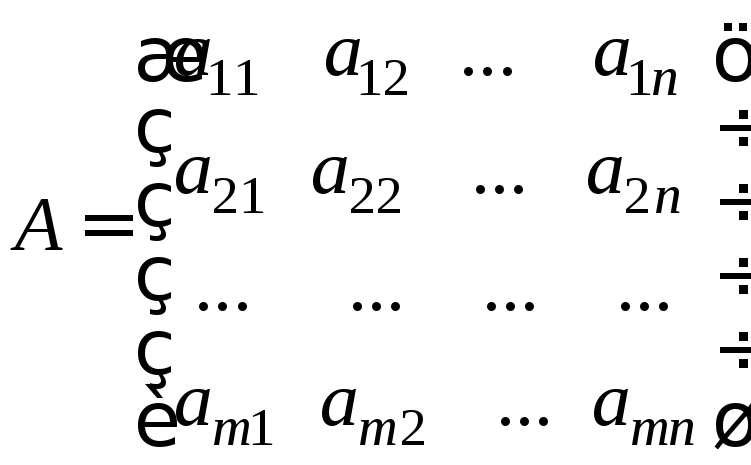 ,
яка складається з коефіцієнтів при
невідомих;
матрицю-стовпець вільних членів:
,
яка складається з коефіцієнтів при
невідомих;
матрицю-стовпець вільних членів:
 ;
матрицю-стовпець невідомих:
;
матрицю-стовпець невідомих: .
.
Використовуючи дії над матрицями, систему рівнянь (1.8) можна записати у матричній формі
![]() .
(1.9)
.
(1.9)
|
|
Розв’язком
системи лінійних рівнянь
(1.8) називають таку сукупність чисел
|
Загальний розв’язок системи передбачає вираз основних невідомих через вільні. Частинний розв’язок одержують із загального наданням вільним змінним певних значень
Розширена
матриця
![]() системи (1.8) або (1.9) складається з матриці
системи (1.8) або (1.9) складається з матриці
![]() і стовпця вільних членів
і стовпця вільних членів![]() і має вигляд (для
зручності стовпець
вільних членів у розширеній матриці
відділяють вертикальною лінією):
і має вигляд (для
зручності стовпець
вільних членів у розширеній матриці
відділяють вертикальною лінією):
 .
.
|
|
Систему рівнянь називають сумісною, якщо вона має хоча б один розв’язок, і несумісною, якщо вона не має жодного розв’язку. |
|
|
Систему називають визначеною, якщо вона має тільки один розв’язок, і невизначеною, якщо система має більше одного розв’язку. |
Однорідна система завжди є сумісною, оскільки завжди має нульовий розв’язок.
Елементарні перетворення системи лінійних рівнянь
|
1) |
додавання до обох частин рівняння відповідних частин другого, помножених на одне число; |
|
2) |
переставлення рівнянь місцями; |
|
3) |
виключення з подальшого розгляду рівнянь, що є тотожностями для всіх значень невідомих змінних. |
Ці елементарні перетворення не змінюють сумісності і розв’язку системи лінійних рівнянь.
Умову сумісності системи лінійних рівнянь характеризує теорема Кронекера-Капеллі (Леопольд Кронекер (1823-1891) ‑ німецький математик).
|
Теорема 1.4. (Кронекера-Капеллі) |
Для
того, щоб система лінійних алгебраїчних
рівнянь (1.8) була сумісною, необхідно
і достатньо, щоб ранг матриці
|
|
Приклад 1.6. |
Перевірити сумісність системи рівнянь
|
Розв’язання.
Випишемо
основну та розширену матриці системи
лінійних рівнянь:
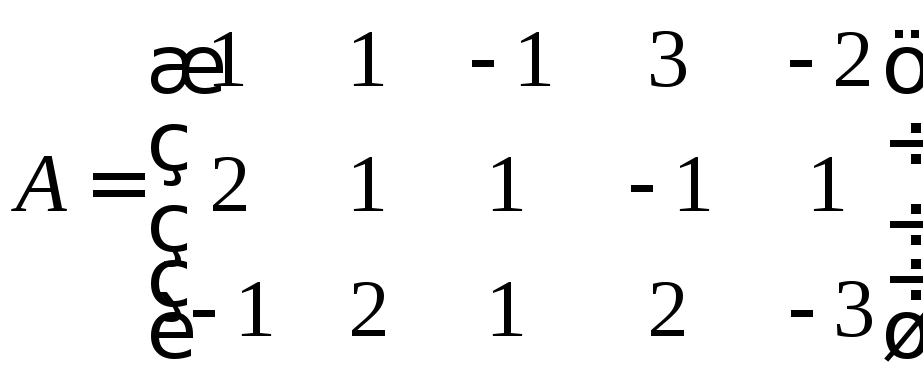 ,
,
 .
.
З
елементів цих двох матриць можна скласти
базисний мінор третього порядку, що не
дорівнює нулю:
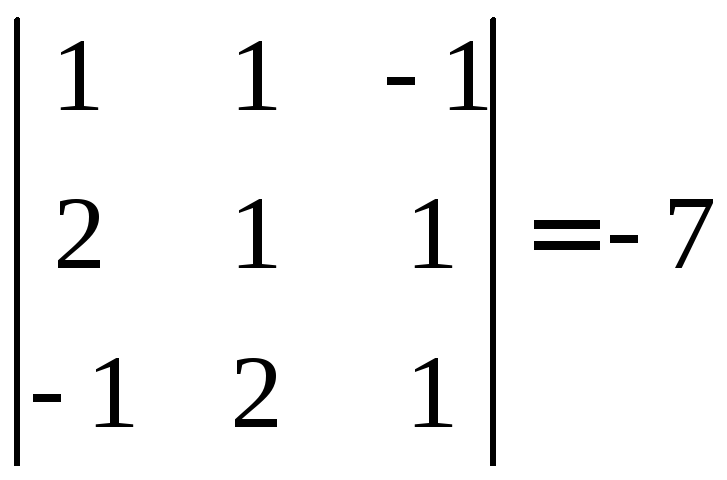 .
.
Отже,
![]() і
і![]() .
Тобто
.
Тобто![]() .
За теоремою Кронекера-Капеллі досліджувана
система лінійних рівнянь є сумісною.
.
За теоремою Кронекера-Капеллі досліджувана
система лінійних рівнянь є сумісною.
Частинним
випадком прямокутної системи (1.8) є
квадратна система рівнянь
![]() .
Тоді матриця системи
.
Тоді матриця системи![]() є квадратною:
є квадратною:
 ,
,
а
її визначник
![]() називаютьосновним
визначником системи.
називаютьосновним
визначником системи.

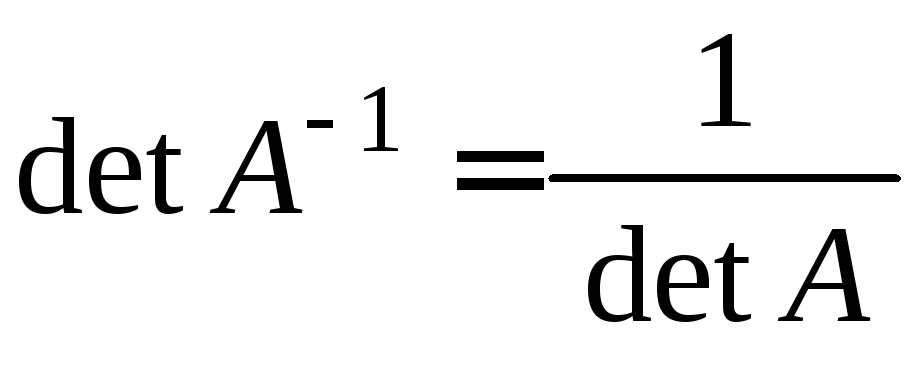 ;
; .
.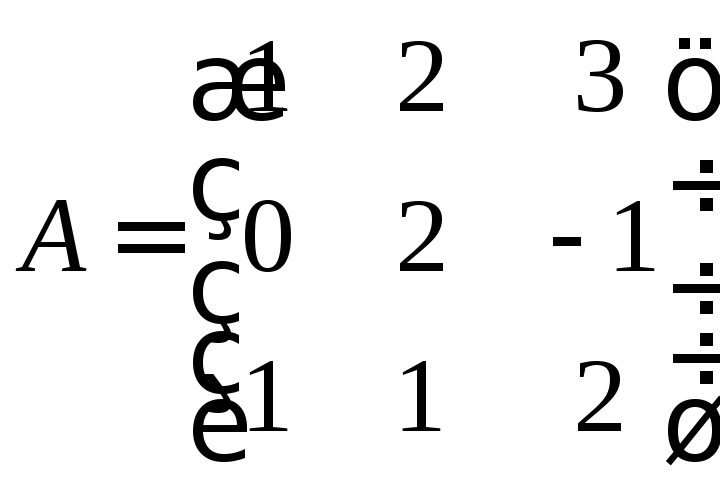 .
. (1.8)
(1.8)