Метод Гаусса

Метод Гаусса – метод послідовного виключення змінних – полягає в тому, що за допомогою елементарних перетворень система рівнянь шляхом послідовного виключення змінних приводиться до рівносильної системи східчастого (або трикутного) виду, з якої, починаючи з останніх (за номером) змінних, знаходять всі інші змінні.

Метод Гаусса є універсальним методом розв’язання систем лінійних рівнянь (1.8). Метод Гаусса реалізується в два етапи, які розділяються на декілька кроків. Перший етап полягає у приведенні системи лінійних рівнянь до трикутного вигляду.

І етап  прямий хід виключень:

І крок  припустимо, що коефіцієнт (у протилежному випадку можна поміняти місцями рівняння у системі). Поділимо перше рівняння наі за його допомогою виключимо з усіх інших рівнянь системи змінну. Для цього слід одержане перше рівняння помножити на, …,та додати відповідно до другого, … ,т-го рівнянь системи. Таким чином одержимо еквівалентну вихідній систему лінійних рівнянь, яка містить змінну тільки у першому рівнянні.

ІІ крок  перше рівняння залишаємо без змін. Далі припустимо, що коефіцієнт при у другому рівнянні одержаної системи відрізняється від нуля. Слід розділити на нього друге рівняння і аналогічно першому кроку виключити зміннуз усіх рівнянь системи. Змінна, таким чином, залишається тільки в першому та другому рівняннях.

ІІІ крок  Перше і друге рівняння залишаються без змін. За основу беруть третє рівняння і за його допомогою виключають змінну .

Процес послідовного виключення змінних продовжується до приведення вихідної системи лінійних рівнянь до системи лінійних рівнянь трикутного вигляду:

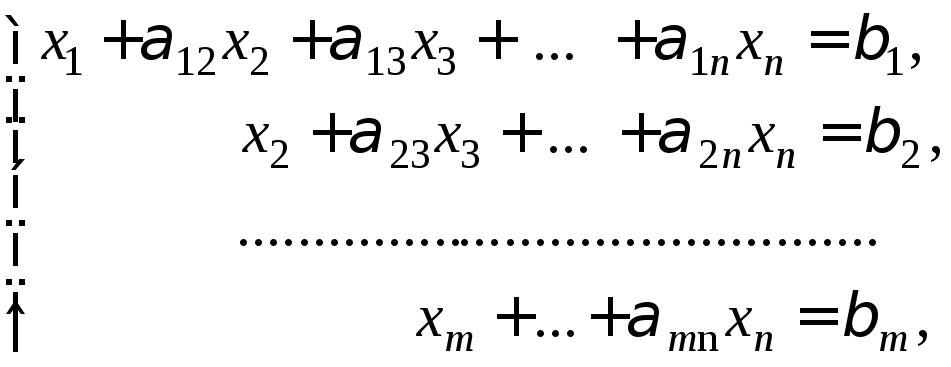(1.13)

де , нові коефіцієнти при невідомих.

Другий етап передбачає знаходження значень невідомих з одержаної системи рівнянь, проводячи рух у протилежному напрямку.

ІІ етап  обернений хід методу Гаусса:

І крок  з останньої рівності модифікованої системи визначаємо вираз змінної через змінні, … ,.

ІІ крок  з передостанньої рівності визначаємо вираз змінної через змінні, … ,з урахуванням виразу змінної.

Далі проводяться аналогічні перетворення для знаходження виразу всіх інших змінних до . В результаті подібних розрахунків одержимо

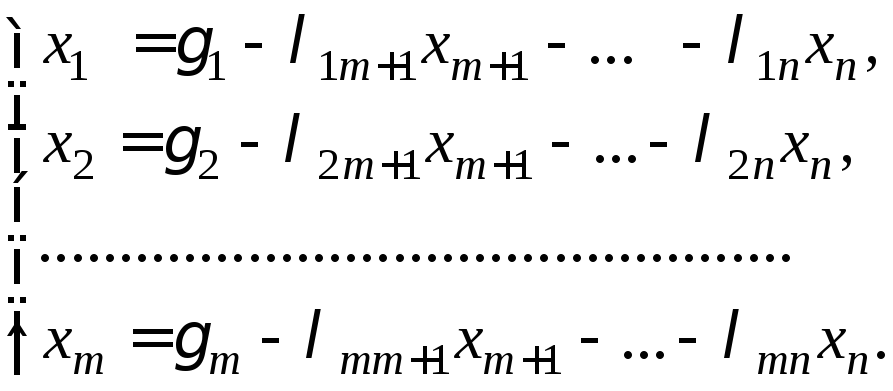(1.14)

Невідомі називаютьбазисними змінними, а невідомі називаютьвільними змінними.

Ранг основної матриці системи (1.8) дорівнює кількості базисних змінних.

Розглянемо застосування цього методу на конкретному прикладі.

Приклад 1.10.

Розв’язати методом Гаусса систему лінійних рівнянь:

Розв’язання. Перший етап: приведемо вихідну систему до трикутного вигляду. Перше і третє рівняння поміняємо місцями і розділимо перше рівняння на :

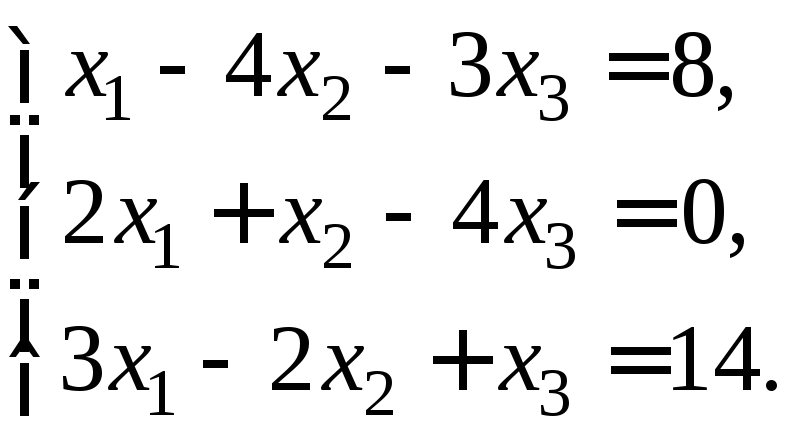
Перше рівняння перепишемо без змін. Помножимо перше рівняння на таі додамо до другого та третього рівнянь:

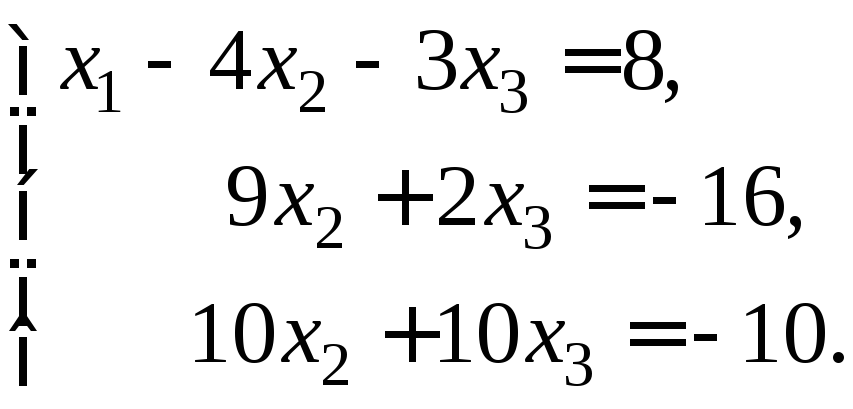
Третє рівняння розділимо на 10 і поміняємо місцями з другим:

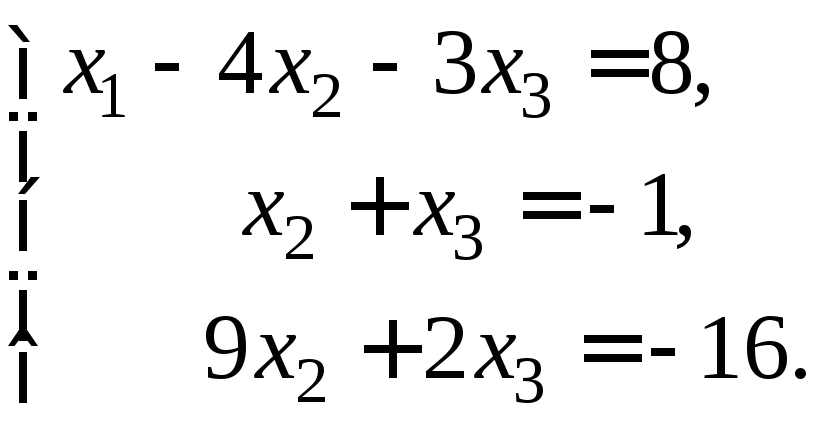
Перше і друге рівняння перепишемо без змін. Друге рівняння помножимо на і додамо до третього:

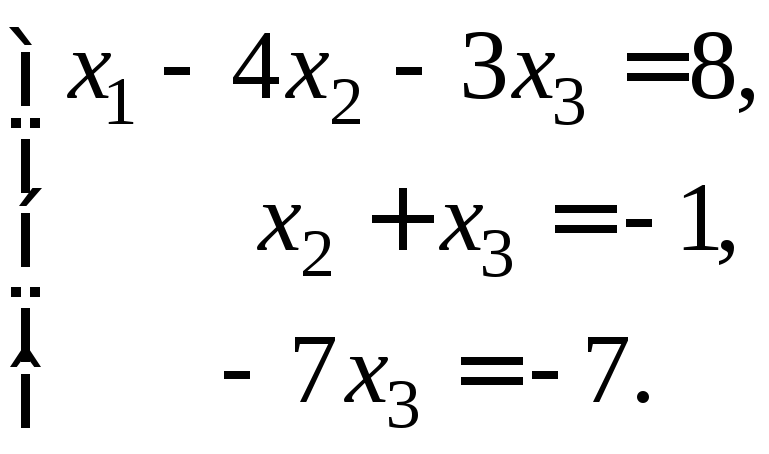
Другий етап: знайдемо значення невідомих. З останньої рівності одержимо і підставимо у друге рівняння, з якого визначимо. Підставимо значенняі в перше рівняння системи і одержимо . Отже, розв’язок вихідної системи є таким:,,.

На практиці зручним виявляється застосовувати ідею методу Гаусса для перетворення елементів розширеної матриці системи лінійних рівнянь, а не до самих рівнянь. Така модифікація методу Гаусса заснована на використанні правила прямокутника.

Прямий хід методу Гаусса, тобто приведення розширеної матриці до трикутного вигляду, реалізується згідно наступного алгоритму.