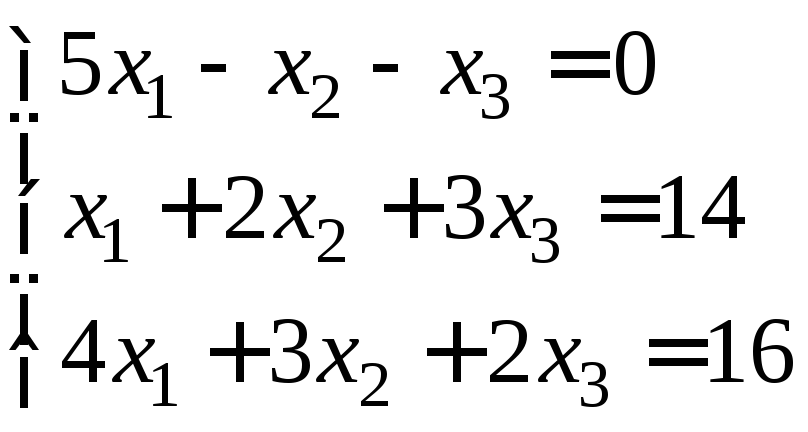- •Міністерство освіти і науки,
- •Правила оформлення контрольної роботи
- •1. Елементи лінійної алгебри
- •1.1. Матриці та дії над ними
- •Дії над матрицями
- •Основні властивості множення матриці на число
- •Основні властивості додавання та віднімання матриць
- •Основні властивості множення матриць
- •Основні властивості транспонування матриці
- •1.2. Визначники та способи їх обчислення
- •Основні властивості визначників
- •Алгоритм обчислення оберненої матриці
- •Властивості обертання невироджених матриць
- •1.3. Системи лінійних рівнянь
- •Елементарні перетворення системи лінійних рівнянь
- •Метод Крамера
- •Метод оберненої матриці
- •Метод Гаусса
- •Алгоритм прямого ходу методу Гаусса
- •2. Елементи аналітичної геометрії
- •2.1. Векторна алгебра
- •Дії над векторами
- •Властивості лінійних операцій над векторами
- •Основні властивості проекцій
- •Дії над векторами в координатній формі
- •Скалярний добуток векторів
- •Основні властивості скалярного добутку векторів
- •Векторний добуток векторів
- •Основні властивості векторного добутку векторів
- •Мішаний добуток векторів
- •Основні властивості мішаного добутку векторів
- •2.2. Пряма на площині
- •Умови взаємного розташування на площині точок і прямих
- •Контрольні питання зі змістового модуля I
- •3. Границя числової послідовності та функції. ОСновні пОняття
- •3.1. Функціональна залежність. Огляд основних елементарних функцій
- •3.2. Границя послідовності та її властивості
- •Основні теореми про послідовності, що збігаються
- •3.3. Нескінченно малі та нескінченно великі послідовності
- •Властивості нескінченно малих послідовностей
- •Властивості нескінченно великих послідовностей
- •Зв’язок між нескінченно великими і нескінченно малими послідовностями
- •3.4. Границя функції та її властивості
- •Односторонні границі функції
- •4. Обчислення границь
- •4.1. Методи розкриття невизначеностей
- •4.2. Визначні границі
- •4.3. Порівняння нескінченно малих функцій
- •Основні еквівалентності при
- •5. Неперервність функції
- •5.1. Неперервність функції в точці і на відрізку
- •Властивості функцій, які неперервні в точці
- •Властивості функцій, що неперервні на відрізку
- •5.2. Класифікація точок розриву
- •Контрольні питання зі змістового модуля II
- •6. Похідна функції однієї змінної
- •6.1. Диференційованість функції однієї змінної. Правила обчислення похідних
- •Правило знаходження похідної
- •Основні властивості похідної
- •6.2. Таблиця похідних основних елементарних функцій. Похідні вищих порядків
- •3 (Куб), ,,,.
- •6.3. Похідні функцій, заданих у параметричній, неявній формах, логарифмічне диференціювання
- •6.4. Диференціал функції однієї змінної
- •7. Диференційованість функції багатьох змінних
- •7.1. Частинні похідні та повний диференціал
- •Повний диференціал першого порядку
- •7.2. Похідна неявної, складної функції. Похідна за напрямом
- •Контрольні питання зі змістового модуля III
Метод Крамера
Метод
Крамера (Габріель Крамер (1704-1752) ‑
швейцарський математик) застосовують
до знаходження розв’язку квадратних
систем лінійних рівнянь. В ньому
застосовують поняття визначника основної
матриці системи
![]() і допоміжних визначників
і допоміжних визначників![]() ,
які отримують з визначника
,
які отримують з визначника![]() заміною першого, другого і так далі до
заміною першого, другого і так далі до![]() го
стовпця на стовпець вільних членів:
го
стовпця на стовпець вільних членів:
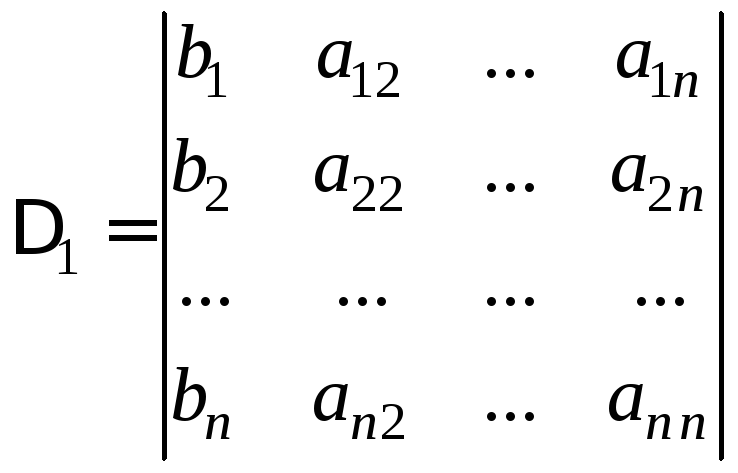 ,
,
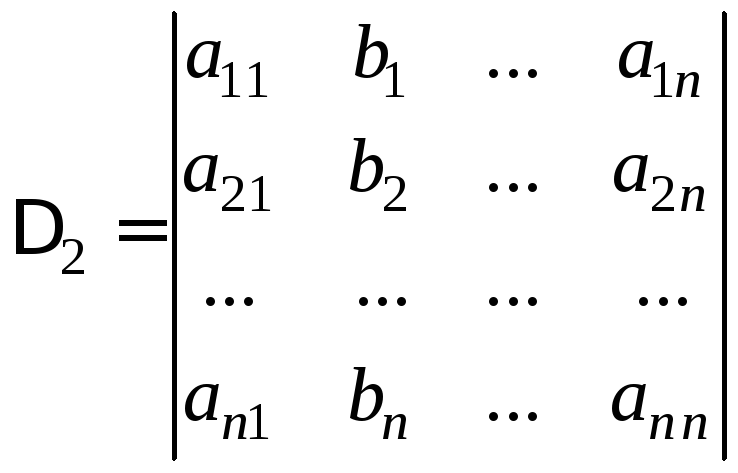 ,
…,
,
…, .
.
Наприклад, для системи, що містить три лінійних рівняння з трьома невідомими
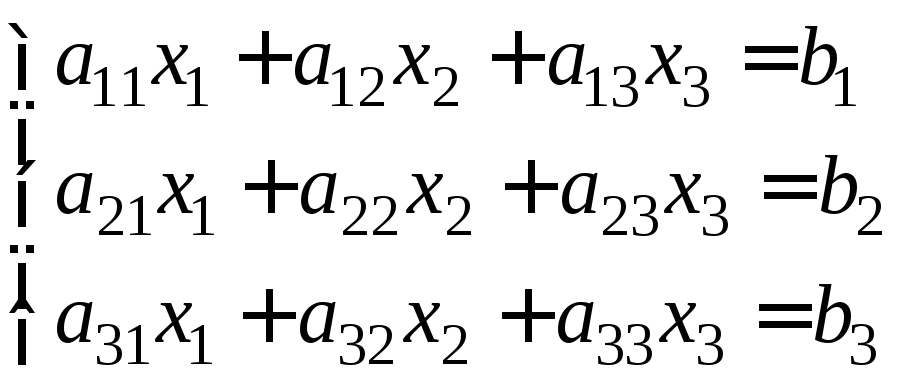 ,
,
маємо:
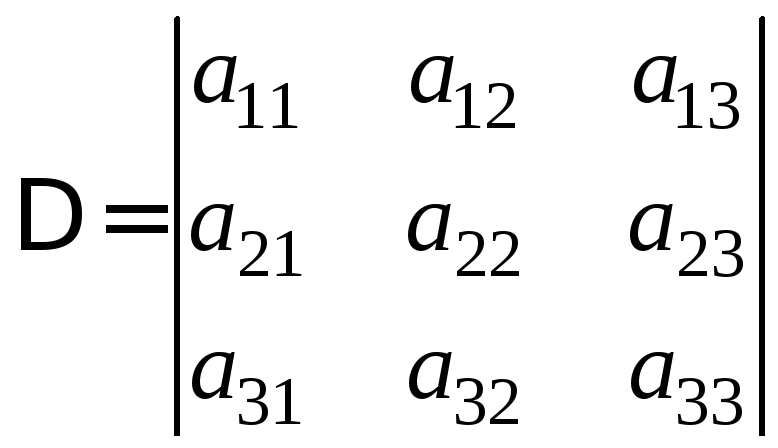 ,
,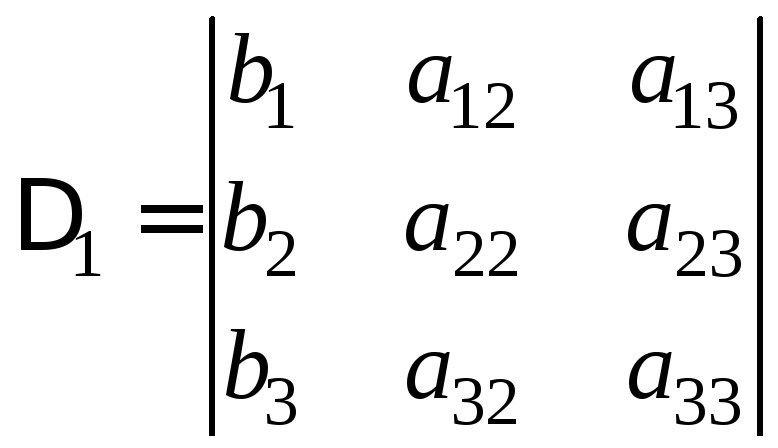 ,
,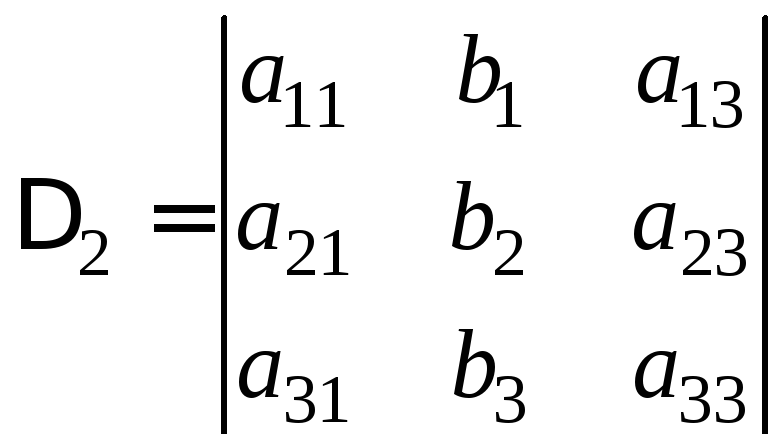 ,
,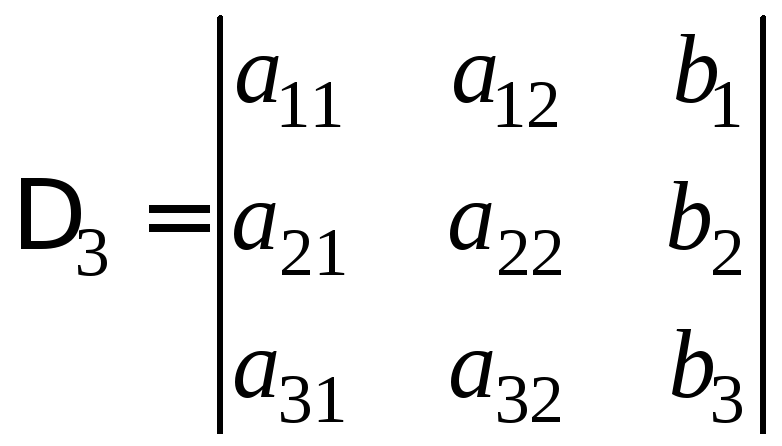 .
.
В залежності від значення визначника основної матриці та значень допоміжних визначників реалізується один з трьох варіантів:
|
1) |
Якщо
визначник основної матриці системи
(1.8) не дорівнює нулю
|
|
2) |
Якщо
основний визначник системи (1.8) дорівнює
нулю
|
|
3) |
Якщо
основний визначник системи (1.8) дорівнює
нулю, а хоча б один з допоміжних
визначників
|
Слід зауважити, що метод Крамера для випадку 2 тільки встановлює існування нескінченної множини розв’язків, але не дає їх виду.
Для
однорідної системи лінійних рівнянь
при
![]() система має єдиний розв’язок
система має єдиний розв’язок![]() .
При
.
При![]() однорідна система має безліч розв’язків.
однорідна система має безліч розв’язків.
|
Приклад 1.7. |
Розв’язати систему лінійних рівнянь методом Крамера
|
Розв’язання.
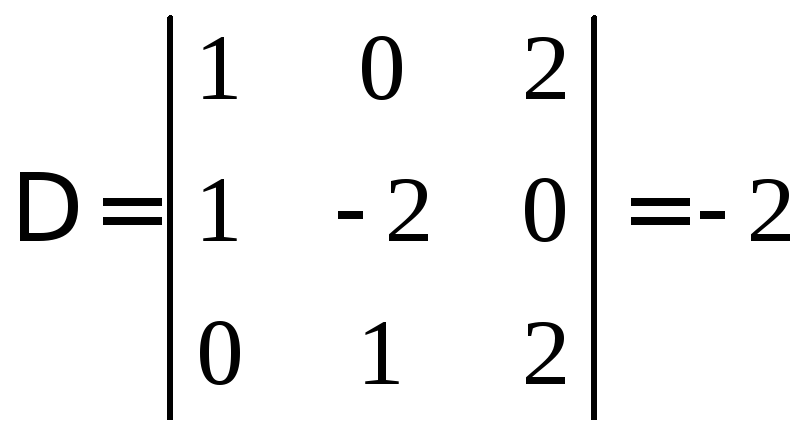
Визначник
основної матриці системи має вид
 .
Оскільки він відрізняється від нуля,
робимо висновок про існування єдиного
розв’язку системи.
.
Оскільки він відрізняється від нуля,
робимо висновок про існування єдиного
розв’язку системи.
Обчислимо допоміжні визначники:
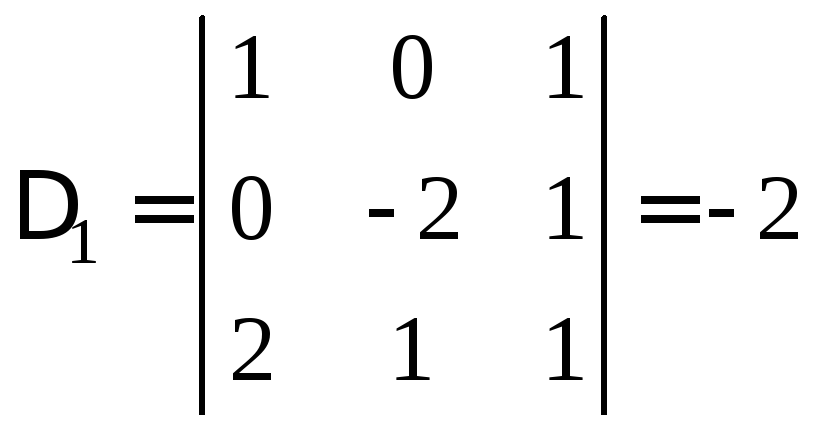 ,
,
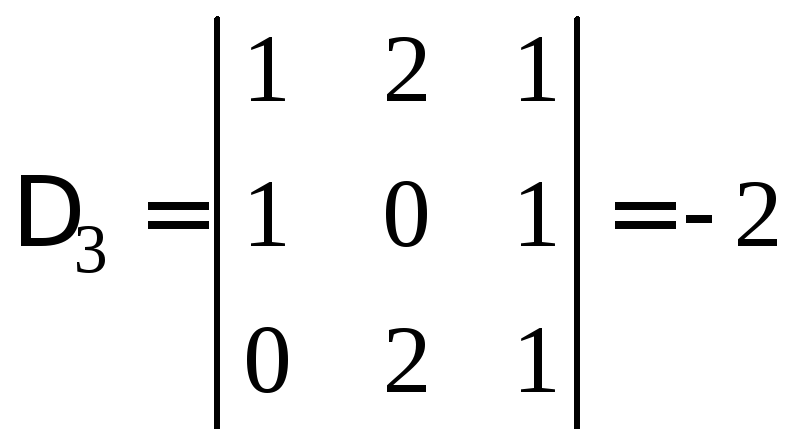 ,
, .
.
За методом Крамера згідно формул (1.10) маємо розв’язок:
![]() .
.
Після знаходження розв’язку системи лінійних рівнянь рекомендується провести перевірку правильності проведених обчислень.
Перевірка:
підстановка у вихідну систему одержаних
значень невідомих
![]() ,
,![]() ,
,![]() призводить до тотожностей:
призводить до тотожностей: що підтверджує правильність отриманого
результату.
що підтверджує правильність отриманого
результату.
Метод оберненої матриці
Матричний метод засновано на використанні властивостей множення матриць. Цей метод є дуже зручним у випадку систем невисокого порядку.
Якщо
основна матриця
![]() системи (1.8) є невиродженою, тобто
системи (1.8) є невиродженою, тобто![]() ,
тоді для неї існує обернена
,
тоді для неї існує обернена![]() .
Помножимо матричну рівність (1.9) зліва
на обернену матрицю
.
Помножимо матричну рівність (1.9) зліва
на обернену матрицю![]() :
:
![]() .
(1.11)
.
(1.11)
З
відношення (1.11) з урахуванням відомої
формули
![]() ,
а також властивостей множення матриць,
а саме
,
а також властивостей множення матриць,
а саме![]() ,
випливає матрична форма розв’язку
системи (1.8):
,
випливає матрична форма розв’язку
системи (1.8):
![]() .
(1.12)
.
(1.12)
Співвідношення (1.11) лежить в основі методу оберненої матриці.
|
Приклад 1.8. |
Розв’язати систему лінійних рівнянь з прикладу 1.7 методом оберненої матриці. |
Розв’язання.
Для основної матриці системи
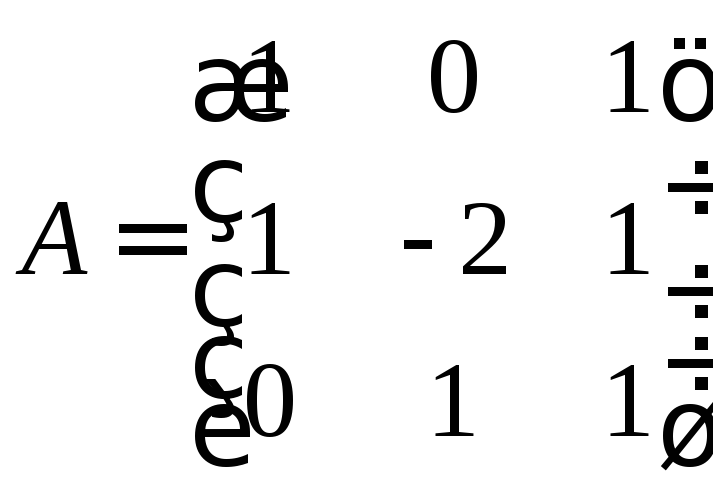 ,
яка єневиродженою,
оскільки
,
яка єневиродженою,
оскільки
![]() ,
обернена буде такою:
,
обернена буде такою:
 .
.
Вектор-стовпець
вільних членів є таким:
 .
Тоді за формулою (1.12) одержимо:
.
Тоді за формулою (1.12) одержимо: .
.
Отже,
![]() .
.
|
Приклад 1.9. |
Розв’язати
матричним методом систему лінійних
рівнянь
|
Розв’язання.
Знайдемо обернену до матриці
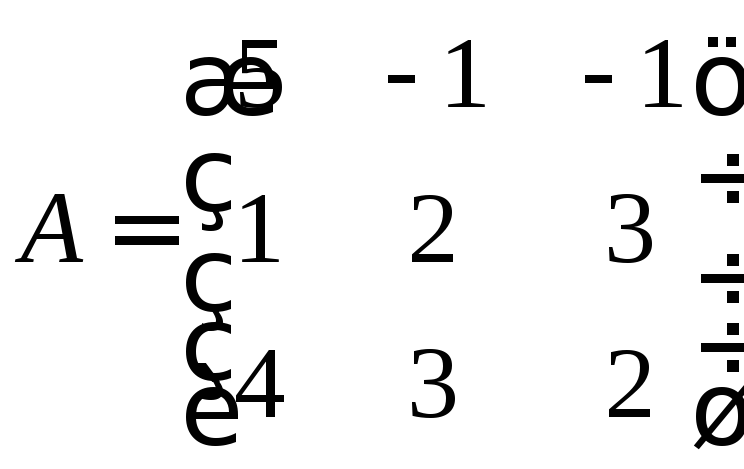 з визначником
з визначником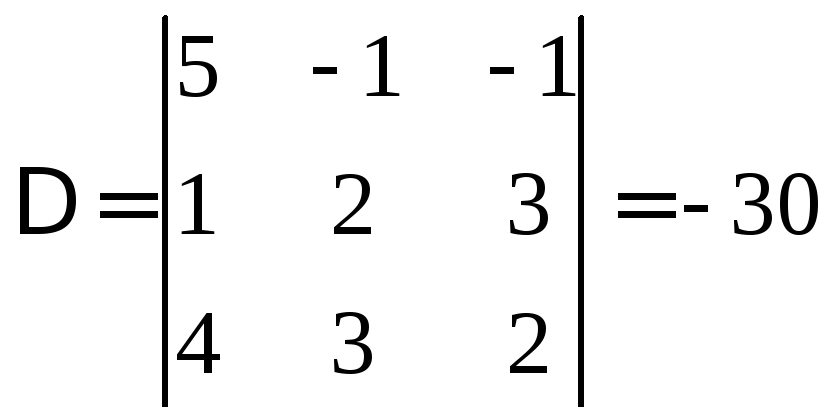 :
: .
.
Тоді
 .
.
Отже,
![]() .
.
Незважаючи на обмеження можливості застосування методу оберненої матриці і складність обчислень при великих значеннях коефіцієнтів, а також систем високого порядку, матричний метод може бути легко реалізованим на ЕОМ.
Метод
оберненої матриці і метод Крамера є
дуже трудомісткими за кількістю
обчислювальної роботи. Тим часом існують
більше економічні методи розв’язання
систем лінійних рівнянь, які опираються
на попереднє перетворення матриці
системи до спеціального виду. Одним із
них є метод Гауса, що застосовується не
тільки у випадку, коли
![]() .
.

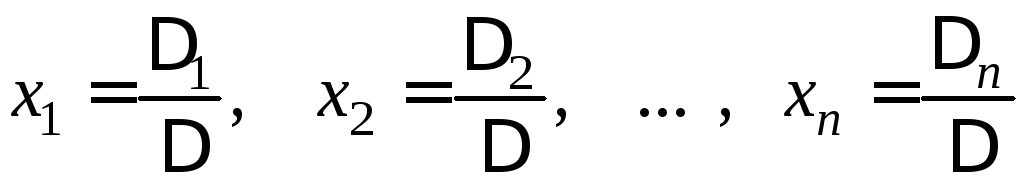 .
(1.10)
.
(1.10)