Дії над матрицями

1.	Множення матриці на число

Щоб помножити матрицю на число, необхідно на це число помножити всі елементи матриці: .

Основні властивості множення матриці на число

1)	;
2)	.

За правилом множення матриці на число індексують економічні показники, приводячи їх до порівнянного виду. Наприклад, щоб виразити запаси тканин в порівнянних цінах, всі значення множать на індекс цін.

Розмірність матриці при множенні її на число не змінюється.

Наприклад, якщ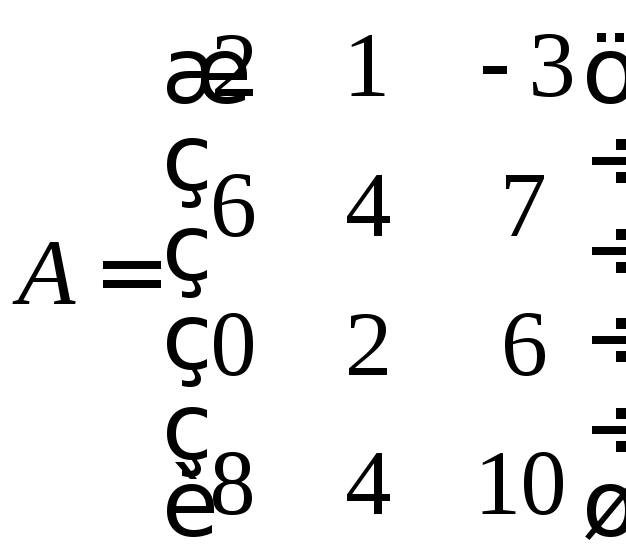о , то.

2.	Додавання та віднімання матриць

Щоб додати (відняти) дві матриці одного порядку, необхідно додати (відняти) всі відповідні елементи цих матриць (елементи з однаковими індексами): .

Основні властивості додавання та віднімання матриць

1)	;
2)	;
3)	;
4)	;
5)	;
6)	.

Наприклад, для матриць ірозмірностісума та різниця мають вид:

, .

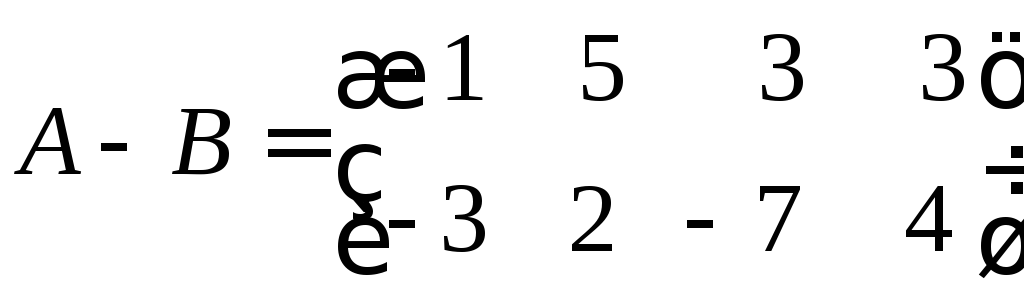За допомогою правила додавання матриць формують різноманітні накопичувані відомості та таблиці.

3.	Множення матриць

Матрицю можна помножити на матрицюі обчислити добуток матрицьтільки у випадку узгодженості цих матриць.

Матрицю називаютьузгодженою з матрицею , якщо кількість стовпців матрицідорівнює кількості рядків матриці.

Наприклад, матриці іє узгодженими тому, що матрицямістить три стовпці, а матриця‑ три рядки.

Зауваження.

Узгодженість матриці з матрицеюне передбачаєвиконання умови узгодженості матриці з матрицею.

Таким чином, перемножити дві матриці можна тільки тоді, коли кількість стовпців першої матриці дорівнює кількості рядків другої. Узгодження розмірностей матриць-множників і матриці добутку можна подати за допомогою наступної схеми:

Отже, в результаті множення матриці на матрицюодержуємо матрицю, кількість рядків в якій дорівнює кількості рядківматриці, а кількість стовпців ‑ кількості стовпцівматриці, тобто матрицямає розмірність.

Якщо перемножуються квадратні матриці іоднакової розмірності, то їх добутокє матрицею тієї ж розмірності.

Щоб знайти елемент добутку, який міститься в-му рядку і-му стовпці, необхідно знайти суму добутків елементів-го рядка матриціна елементи-го стовпця матриці: .

Основні властивості множення матриць

1)	;
2)	, ;
3)	, ;
4)	;
5)	;
6)	;
7)	.

Приклад 1.1.

Перевірити узгодженість і знайти добуток матриць і, якщо,.

Розв’язання. Розмірності матриць-множників: ‑,‑. Вони визначають виконання умови узгодженості матриціз матрицею. Тобто добутокіснує і має розмірність. Проведемо обчислення добутку матрицьі:

Зауважимо, що у даному випадку не існує, бо матрицяне є узгодженою з матрицею.

Приклад 1.2.

Знайти добутки таматриці-рядкаі матриці-стовпця.

Розв’язання. Очевидно, що матриця узгоджена з матрицею, і навпаки матрицяє узгодженою з матрицею.

;

.

Отже, у першому випадку добуток є матрицею розмірності , а у другому це матриця порядку , тобто скалярна величина.

Зауваження.

Добуток двох ненульових матриць може дорівнювати нульовій матриці, тобто з того, що , не випливає, що, або.

Наприклад, 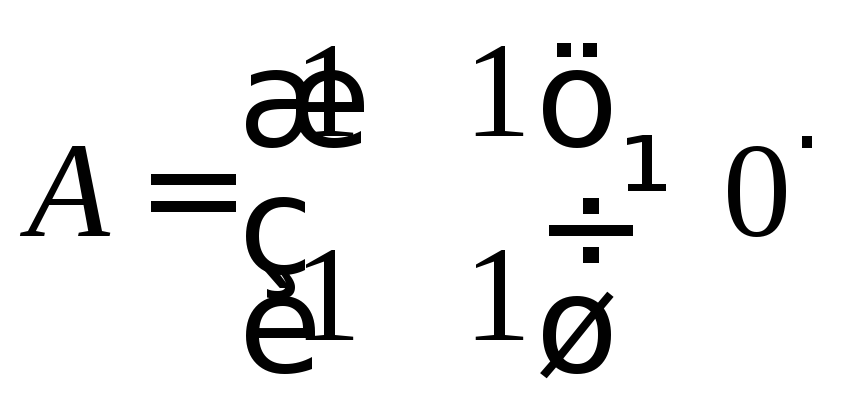,, але.

Для знаходження цілого додатного степеня квадратної матриціслід знайти добутокматриць: .

Наприклад, для обчислення , депотрібно знайти добуток.

Зауваження.

Операція піднесення до степеня визначається тільки для квадратних матриць.

4.	Транспонування матриці

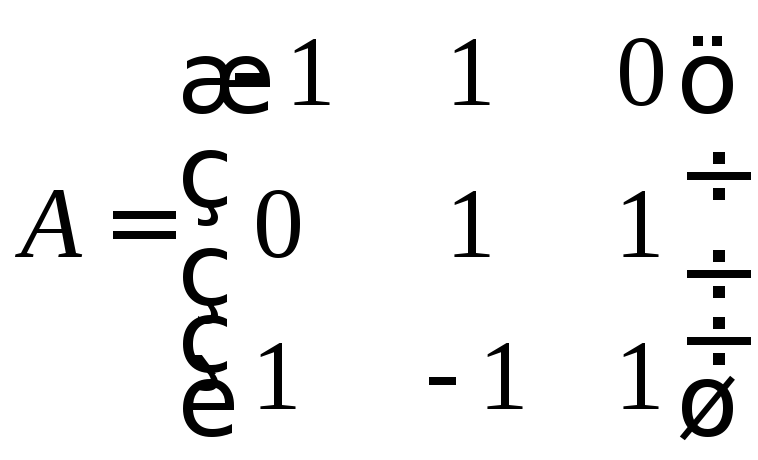Щоб транспонувати матрицю , треба поміняти місцями її рядки зі стовпцями. Транспоновану матрицю позначають символом. Якщо вихідна матрицямає розмірність, то розмірність транспонованої матрицібуде.