
- •Міністерство освіти і науки,
- •Правила оформлення контрольної роботи
- •1. Елементи лінійної алгебри
- •1.1. Матриці та дії над ними
- •Дії над матрицями
- •Основні властивості множення матриці на число
- •Основні властивості додавання та віднімання матриць
- •Основні властивості множення матриць
- •Основні властивості транспонування матриці
- •1.2. Визначники та способи їх обчислення
- •Основні властивості визначників
- •Алгоритм обчислення оберненої матриці
- •Властивості обертання невироджених матриць
- •1.3. Системи лінійних рівнянь
- •Елементарні перетворення системи лінійних рівнянь
- •Метод Крамера
- •Метод оберненої матриці
- •Метод Гаусса
- •Алгоритм прямого ходу методу Гаусса
- •2. Елементи аналітичної геометрії
- •2.1. Векторна алгебра
- •Дії над векторами
- •Властивості лінійних операцій над векторами
- •Основні властивості проекцій
- •Дії над векторами в координатній формі
- •Скалярний добуток векторів
- •Основні властивості скалярного добутку векторів
- •Векторний добуток векторів
- •Основні властивості векторного добутку векторів
- •Мішаний добуток векторів
- •Основні властивості мішаного добутку векторів
- •2.2. Пряма на площині
- •Умови взаємного розташування на площині точок і прямих
- •Контрольні питання зі змістового модуля I
- •3. Границя числової послідовності та функції. ОСновні пОняття
- •3.1. Функціональна залежність. Огляд основних елементарних функцій
- •3.2. Границя послідовності та її властивості
- •Основні теореми про послідовності, що збігаються
- •3.3. Нескінченно малі та нескінченно великі послідовності
- •Властивості нескінченно малих послідовностей
- •Властивості нескінченно великих послідовностей
- •Зв’язок між нескінченно великими і нескінченно малими послідовностями
- •3.4. Границя функції та її властивості
- •Односторонні границі функції
- •4. Обчислення границь
- •4.1. Методи розкриття невизначеностей
- •4.2. Визначні границі
- •4.3. Порівняння нескінченно малих функцій
- •Основні еквівалентності при
- •5. Неперервність функції
- •5.1. Неперервність функції в точці і на відрізку
- •Властивості функцій, які неперервні в точці
- •Властивості функцій, що неперервні на відрізку
- •5.2. Класифікація точок розриву
- •Контрольні питання зі змістового модуля II
- •6. Похідна функції однієї змінної
- •6.1. Диференційованість функції однієї змінної. Правила обчислення похідних
- •Правило знаходження похідної
- •Основні властивості похідної
- •6.2. Таблиця похідних основних елементарних функцій. Похідні вищих порядків
- •3 (Куб), ,,,.
- •6.3. Похідні функцій, заданих у параметричній, неявній формах, логарифмічне диференціювання
- •6.4. Диференціал функції однієї змінної
- •7. Диференційованість функції багатьох змінних
- •7.1. Частинні похідні та повний диференціал
- •Повний диференціал першого порядку
- •7.2. Похідна неявної, складної функції. Похідна за напрямом
- •Контрольні питання зі змістового модуля III
7. Диференційованість функції багатьох змінних
7.1. Частинні похідні та повний диференціал
Дотепер ми розглядали функції, які мали один аргумент.
|
|
Нехай
кожній точці
Тоді
відповідність (7.1) називають функцією
двох змінних,
а множину значень
|
Для
функції двох змінних область визначення,
взагалі кажучи, є деякою областю площини
![]() .
А графічне зображення самої функції
(7.1) визначає, взагалі кажучи, деяку
поверхню в трьохвимірному просторі
.
А графічне зображення самої функції
(7.1) визначає, взагалі кажучи, деяку
поверхню в трьохвимірному просторі![]() .
.
Аналогічно можна ввести в розгляд функцію декількох змінних.
Розглянемо
функцію
![]() і точку
і точку![]() з області її визначення.
Станемо змінювати координату
з області її визначення.
Станемо змінювати координату
![]() ,
залишаючи значення
,
залишаючи значення![]() постійним. В результаті отримаємо
функцію
постійним. В результаті отримаємо
функцію![]() від однієї змінної
від однієї змінної![]() .
.
Надамо
величині
![]() приросту
приросту![]() таким чином, що точка
таким чином, що точка![]() теж
буде належати області визначення функції
(7.1). Складемо
різницю
теж
буде належати області визначення функції
(7.1). Складемо
різницю
![]() ,
,
яку
називають частинним
приростом функції (7.1)
по аргументу
![]() в точці
в точці![]() .
.
|
|
Якщо існує скінченна границя
то
її називають частинною
похідною
від
функції
|
Аналогічно
вводимо частинний
приріст функції по аргументу
![]() в точці
в точці![]() :
:
![]() .
.
|
|
Якщо існує скінчена границя
то
її називають частинною
похідною від функції
|
Правило
обчислення частинних похідних: частинні
похідні обчислюють за відомими правилами
диференціювання функції однієї змінної;
при обчисленні
![]() вважають
вважають![]() постійною величиною; при обчисленні
постійною величиною; при обчисленні![]() постійним слід вважати
постійним слід вважати![]() .
.
|
Приклад 7.1. |
Знайти
частинні похідні функцій: а) |
Розв’язання.
а)
![]() ,
,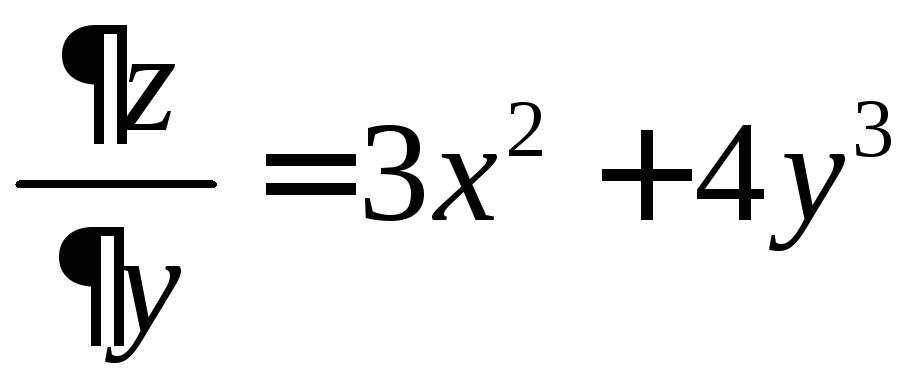 ;
;
б)
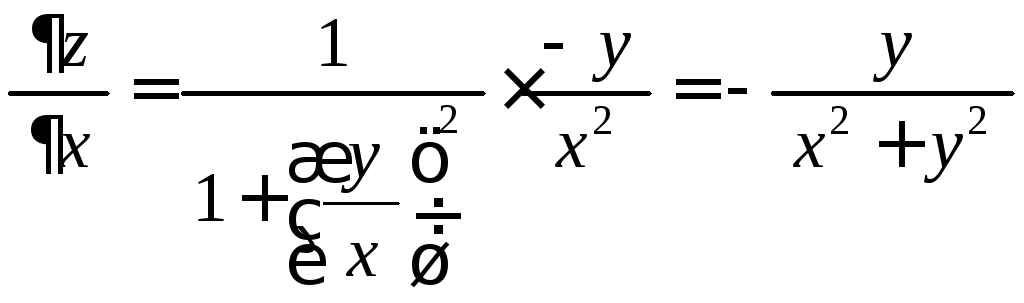 ,
, ;
;
в)
![]() ,
,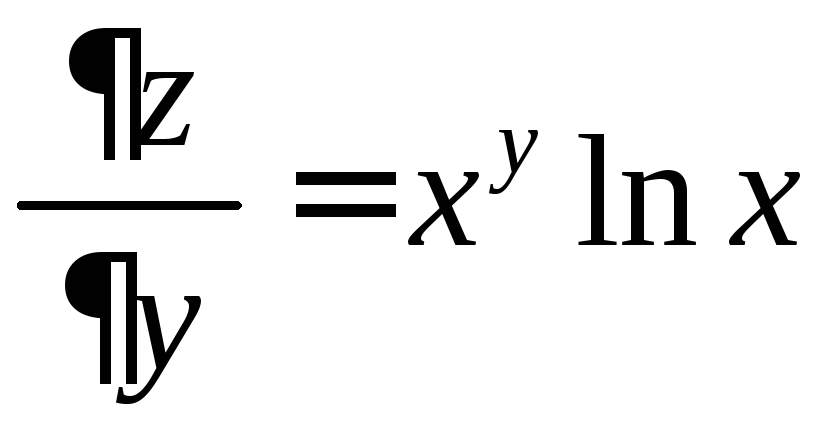 .
.
Геометричний
зміст частинних похідних функції
![]() :
:
|
|
Частинна
похідна
|
|
|
Частинна
похідна
|
Крива
![]() визначається як перетин поверхні
визначається як перетин поверхні![]() площиною
площиною![]() ,
а крива
,
а крива![]() є перетином цієї поверхні площиною
є перетином цієї поверхні площиною![]() .
.
|
|
Розглянемо
функцію
|
|
Приклад 7.2. |
Визначити
частинну похідну функції
|
Розв’язання.
![]() .
.
|
|
Частинні
похідні
Похідні від частинних похідних другого порядку називають частинними похідними третього порядку. |
Аналогічно визначають частинні похідні будь-якого порядку. Частинну похідну порядку вище першого по різним змінним називають змішаною.
|
Приклад 7.3. |
Обчислити
частинні похідні другого порядку
функції
|
Розв’язання. Визначимо спочатку частинні похідні першого порядку:
![]() ,
,
![]() .
.
Частинні похідні другого порядку мають вигляд:
![]() ,
,
![]() ,
,![]() ,
,![]() .
.
Порівнюючи
змішані похідні, бачимо, що вони
співпадають:
![]() .
Цей факт не є випадковим.
.
Цей факт не є випадковим.
|
Теорема 7.1. |
(про
змішані похідні)
Нехай функція
|
Справедливим також є наступний факт: дві неперервні частинні похідні одного порядку, що відрізняються лише порядком виконання операцій диференціювання, але не кількістю цих операцій для кожного з аргументів, будуть рівними між собою.
Таким чином, значення будь-якої змішаної частинної похідної елементарної функції не залежить від порядку диференціювання.
Наприклад,
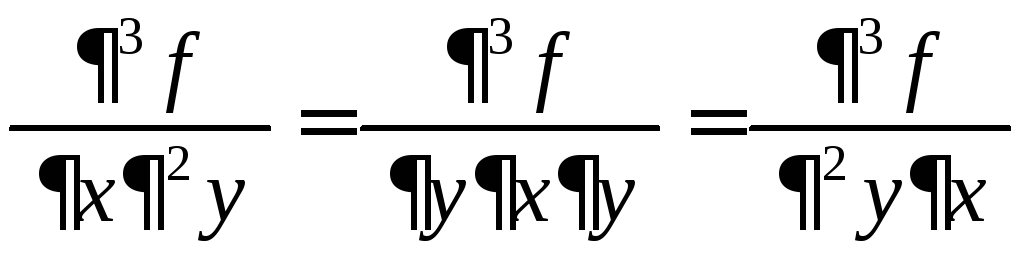 .
.

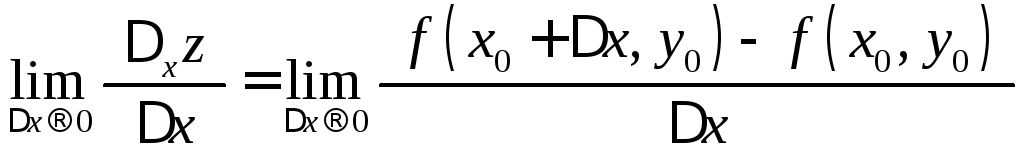 ,
,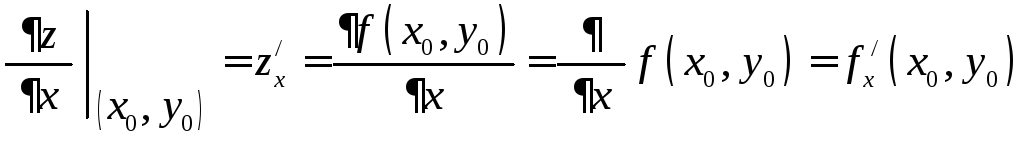 .
.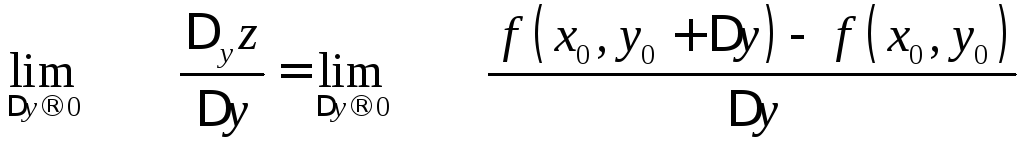 ,
,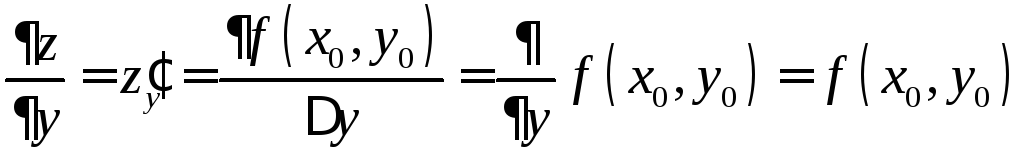 .
.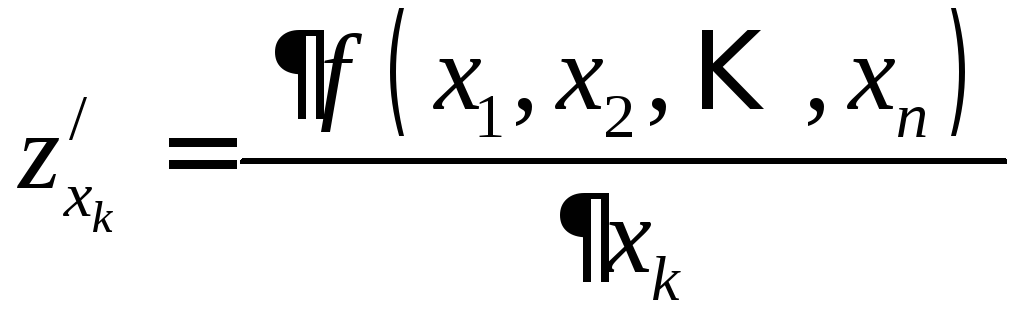 називають звичайну похідну по змінній
називають звичайну похідну по змінній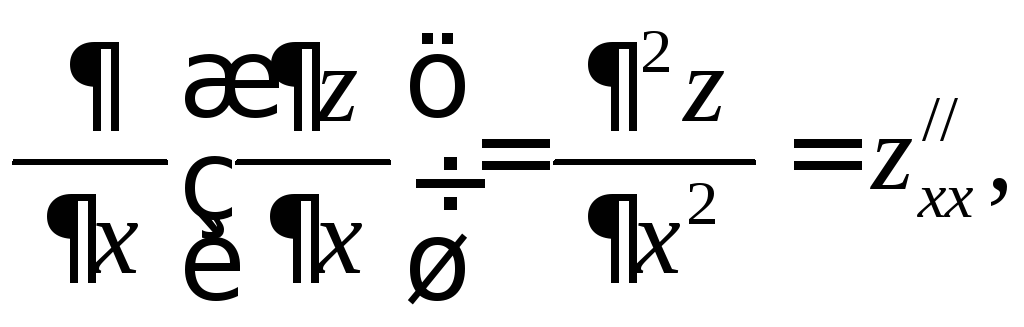
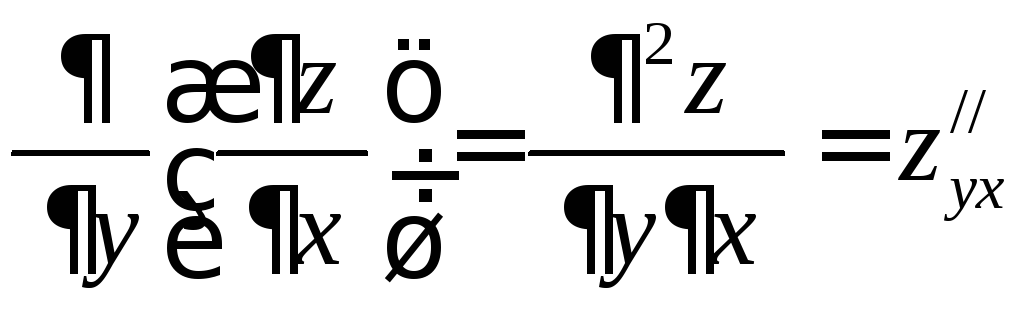 ,
,
 .
.