
- •Міністерство освіти і науки,
- •Правила оформлення контрольної роботи
- •1. Елементи лінійної алгебри
- •1.1. Матриці та дії над ними
- •Дії над матрицями
- •Основні властивості множення матриці на число
- •Основні властивості додавання та віднімання матриць
- •Основні властивості множення матриць
- •Основні властивості транспонування матриці
- •1.2. Визначники та способи їх обчислення
- •Основні властивості визначників
- •Алгоритм обчислення оберненої матриці
- •Властивості обертання невироджених матриць
- •1.3. Системи лінійних рівнянь
- •Елементарні перетворення системи лінійних рівнянь
- •Метод Крамера
- •Метод оберненої матриці
- •Метод Гаусса
- •Алгоритм прямого ходу методу Гаусса
- •2. Елементи аналітичної геометрії
- •2.1. Векторна алгебра
- •Дії над векторами
- •Властивості лінійних операцій над векторами
- •Основні властивості проекцій
- •Дії над векторами в координатній формі
- •Скалярний добуток векторів
- •Основні властивості скалярного добутку векторів
- •Векторний добуток векторів
- •Основні властивості векторного добутку векторів
- •Мішаний добуток векторів
- •Основні властивості мішаного добутку векторів
- •2.2. Пряма на площині
- •Умови взаємного розташування на площині точок і прямих
- •Контрольні питання зі змістового модуля I
- •3. Границя числової послідовності та функції. ОСновні пОняття
- •3.1. Функціональна залежність. Огляд основних елементарних функцій
- •3.2. Границя послідовності та її властивості
- •Основні теореми про послідовності, що збігаються
- •3.3. Нескінченно малі та нескінченно великі послідовності
- •Властивості нескінченно малих послідовностей
- •Властивості нескінченно великих послідовностей
- •Зв’язок між нескінченно великими і нескінченно малими послідовностями
- •3.4. Границя функції та її властивості
- •Односторонні границі функції
- •4. Обчислення границь
- •4.1. Методи розкриття невизначеностей
- •4.2. Визначні границі
- •4.3. Порівняння нескінченно малих функцій
- •Основні еквівалентності при
- •5. Неперервність функції
- •5.1. Неперервність функції в точці і на відрізку
- •Властивості функцій, які неперервні в точці
- •Властивості функцій, що неперервні на відрізку
- •5.2. Класифікація точок розриву
- •Контрольні питання зі змістового модуля II
- •6. Похідна функції однієї змінної
- •6.1. Диференційованість функції однієї змінної. Правила обчислення похідних
- •Правило знаходження похідної
- •Основні властивості похідної
- •6.2. Таблиця похідних основних елементарних функцій. Похідні вищих порядків
- •3 (Куб), ,,,.
- •6.3. Похідні функцій, заданих у параметричній, неявній формах, логарифмічне диференціювання
- •6.4. Диференціал функції однієї змінної
- •7. Диференційованість функції багатьох змінних
- •7.1. Частинні похідні та повний диференціал
- •Повний диференціал першого порядку
- •7.2. Похідна неявної, складної функції. Похідна за напрямом
- •Контрольні питання зі змістового модуля III
Основні теореми про послідовності, що збігаються
|
Теорема 3.1. |
Послідовність, що збігається, має тільки одну границю. |
|
Теорема 3.2. |
Послідовність, що збігається, обмежена. |
|
Теорема 3.3. |
Границя алгебраїчної суми скінченого числа послідовностей дорівнює такій же алгебраїчній сумі границь кожної з послідовностей:
|
|
Теорема 3.4. |
Границя добутку скінченого числа послідовностей дорівнює добутку границь цих послідовностей:
|
|
Теорема 3.5. |
Постійну величину можна виносити за знак границі послідовності:
|
|
Теорема 3.6. |
Границя
відношення двох послідовностей
|
|
Теорема 3.7. |
Якщо
для послідовностей {xn},
{yn}
починаючи з деякого номера, виконується
нерівність
|
|
Теорема 3.8.
|
(ознака існування границі послідовності) Якщо послідовність монотонна і обмежена, то вона має границю. |
|
Теорема 3.9. |
Якщо
для послідовностей {xn},
{yn},
{zn},
починаючи з деякого номера, виконується
нерівність
|
3.3. Нескінченно малі та нескінченно великі послідовності
Серед функцій натурального аргументу особливе місце належить нескінченно малим і нескінченно великим послідовностям.
|
|
Послідовність
хn
називають
нескінченно
малою,
якщо
|
Отже, члени послідовності {хn}, починаючи з певного номера і для всіх наступних номерів, необмежено наближаються до нуля.
|
Зауваження. |
Не слід плутати нескінченно малу послідовність з досить маленьким числом. Дуже мала величина постійна, наприклад, 0,0001; 0,00003. Нескінченно мала послідовність – величина змінна і постійно зменшується. Ніяка постійна (окрім нуля) не може вважатися нескінченно малою. Окремі члени нескінченно малої числової послідовності можуть бути скільки завгодно великими. |
Наприклад,
послідовність
![]() є нескінченно малою, оскільки
є нескінченно малою, оскільки![]() приn,
більшому, ніж, наприклад, числа 1010/.
Але окремі її значення
приn,
більшому, ніж, наприклад, числа 1010/.
Але окремі її значення
![]() ,
,![]() ,
,![]() не є малими числами.
не є малими числами.
Приклади
нескінченно малих послідовностей:
![]() ,
,
 ,
,
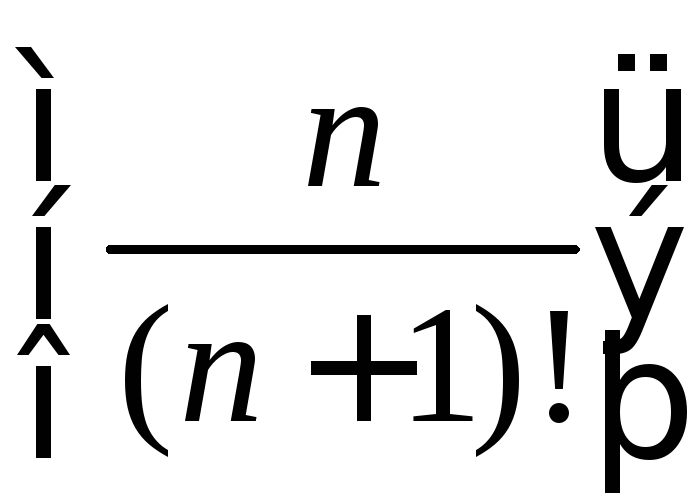 .
.
Властивості нескінченно малих послідовностей
|
1) |
Нескінченно мала послідовність обмежена. |
|
2) |
Сума скінченого числа нескінченно малих послідовностей є нескінченно малою послідовністю. |
|
3) |
Добуток нескінченно малої послідовності на обмежену послідовність або на постійне число є нескінченно малою послідовністю. |
|
4) |
Добуток скінченого числа нескінченно малих послідовностей є нескінченно малою послідовністю. |
|
Зауваження. |
Відношення
двох нескінченно малих величин може
бути величиною скінченою, нескінченно
малою і нескінченно великою. Відношення
двох нескінченно малих величин є
“невизначеністю” вигляду
| |
|
Теорема 3.10. |
Для
того, щоб послідовність {xn}
збігалася до числа
| |
З теореми 3.10 витікає, що послідовність, що має границю, можна подати у вигляді суми постійної (границі а) і нескінченно малої:
![]() .
.
|
|
Послідовність
{xn}
називають нескінченно
великою,
якщо для будь-якого (навіть скільки
завгодно великого) числа
|
Для
позначення нескінченно великої
послідовності {xn}
використовують запис
![]() ,
або
,
або![]() при
при![]() .
.
Якщо,
починаючи з деякого номера N,
члени нескінченно великої послідовності
набувають тільки від’ємних значень,
то пишуть![]() або
або
![]() при
при
![]() .
Якщо, починаючи з деякого номера N,
члени нескінченно великої послідовності
набувають тільки додатних значень, то
пишуть
.
Якщо, починаючи з деякого номера N,
члени нескінченно великої послідовності
набувають тільки додатних значень, то
пишуть![]() або
або
![]() при
при
![]() .
.
|
Зауваження. |
Символ
“ |
|
Зауваження. |
Не слід плутати поняття дуже великої величини і нескінченно великої послідовності. Дуже велика величина є постійною, наприклад 1000000, 10010. Нескінченно велика – змінна. |
Приклади
нескінченно великих послідовностей:
![]() ,
,![]() ,
,![]() .
.

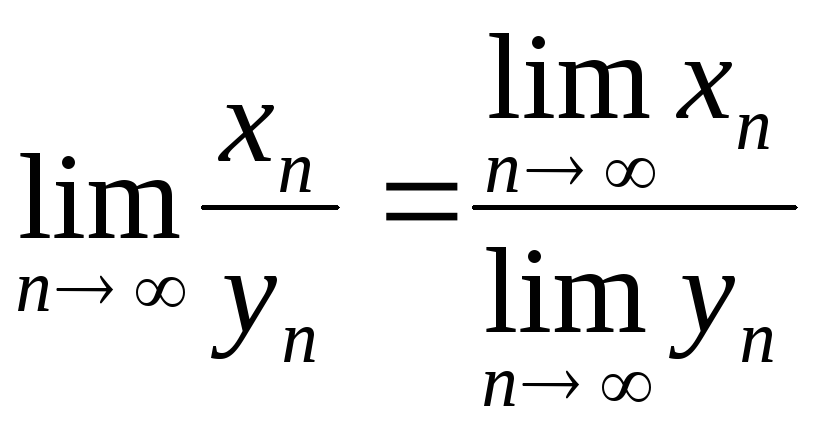 ,
,