
- •Міністерство освіти і науки,
- •Правила оформлення контрольної роботи
- •1. Елементи лінійної алгебри
- •1.1. Матриці та дії над ними
- •Дії над матрицями
- •Основні властивості множення матриці на число
- •Основні властивості додавання та віднімання матриць
- •Основні властивості множення матриць
- •Основні властивості транспонування матриці
- •1.2. Визначники та способи їх обчислення
- •Основні властивості визначників
- •Алгоритм обчислення оберненої матриці
- •Властивості обертання невироджених матриць
- •1.3. Системи лінійних рівнянь
- •Елементарні перетворення системи лінійних рівнянь
- •Метод Крамера
- •Метод оберненої матриці
- •Метод Гаусса
- •Алгоритм прямого ходу методу Гаусса
- •2. Елементи аналітичної геометрії
- •2.1. Векторна алгебра
- •Дії над векторами
- •Властивості лінійних операцій над векторами
- •Основні властивості проекцій
- •Дії над векторами в координатній формі
- •Скалярний добуток векторів
- •Основні властивості скалярного добутку векторів
- •Векторний добуток векторів
- •Основні властивості векторного добутку векторів
- •Мішаний добуток векторів
- •Основні властивості мішаного добутку векторів
- •2.2. Пряма на площині
- •Умови взаємного розташування на площині точок і прямих
- •Контрольні питання зі змістового модуля I
- •3. Границя числової послідовності та функції. ОСновні пОняття
- •3.1. Функціональна залежність. Огляд основних елементарних функцій
- •3.2. Границя послідовності та її властивості
- •Основні теореми про послідовності, що збігаються
- •3.3. Нескінченно малі та нескінченно великі послідовності
- •Властивості нескінченно малих послідовностей
- •Властивості нескінченно великих послідовностей
- •Зв’язок між нескінченно великими і нескінченно малими послідовностями
- •3.4. Границя функції та її властивості
- •Односторонні границі функції
- •4. Обчислення границь
- •4.1. Методи розкриття невизначеностей
- •4.2. Визначні границі
- •4.3. Порівняння нескінченно малих функцій
- •Основні еквівалентності при
- •5. Неперервність функції
- •5.1. Неперервність функції в точці і на відрізку
- •Властивості функцій, які неперервні в точці
- •Властивості функцій, що неперервні на відрізку
- •5.2. Класифікація точок розриву
- •Контрольні питання зі змістового модуля II
- •6. Похідна функції однієї змінної
- •6.1. Диференційованість функції однієї змінної. Правила обчислення похідних
- •Правило знаходження похідної
- •Основні властивості похідної
- •6.2. Таблиця похідних основних елементарних функцій. Похідні вищих порядків
- •3 (Куб), ,,,.
- •6.3. Похідні функцій, заданих у параметричній, неявній формах, логарифмічне диференціювання
- •6.4. Диференціал функції однієї змінної
- •7. Диференційованість функції багатьох змінних
- •7.1. Частинні похідні та повний диференціал
- •Повний диференціал першого порядку
- •7.2. Похідна неявної, складної функції. Похідна за напрямом
- •Контрольні питання зі змістового модуля III
3.2. Границя послідовності та її властивості
Першу спробу створити теорію границь зробив Ньютон у 1686 р., хоча операція граничного переходу застосовувалася і раніше, починаючи із старогрецьких учених. Близьке до сучасного поняття границі сформулював у 1765 р. французький математик і філософ Ж. Даламбер.
Якщо
кожному натуральному числу
![]() поставлене
у відповідність деяке дійсне число хn,
то говорять, що задано послідовність
чисел
х1,
х2,
…, хn,
… Інші позначення: {хn},
хn.
поставлене
у відповідність деяке дійсне число хn,
то говорять, що задано послідовність
чисел
х1,
х2,
…, хn,
… Інші позначення: {хn},
хn.
|
|
Числовою
послідовністю
Числа
х1,
х2,…
називають членами
(елементами)
послідовності,
|
Наприклад,
розглянемо послідовність
![]() .
Загальний член її ‑
.
Загальний член її ‑![]() .
Перші п’ять членів такі:х1
=
1, х2
=
.
Перші п’ять членів такі:х1
=
1, х2
=
![]() ,х3
=
,х3
=
![]() ,х4
=
,х4
=
![]() ,х5
=
,х5
=
![]() .
.
Наприклад,
членами послідовності
![]() є числа
є числа![]()
Прикладом
послідовності є нескінченно спадаюча
геометрична прогресія
![]() ,
де
,
де![]() .
.
|
|
Число
а
називають границею
послідовності
{хn},
якщо для будь-якого наперед заданого
(навіть скільки завгодно малого) числа
|
Для
позначення границі
![]() послідовності {хn}
використовується запис:
послідовності {хn}
використовується запис:
![]() =
а,
або
=
а,
або
![]() при
при
![]() .
.
Інтервал
виду
![]() ,
де
,
де![]()
![]() ,
називають-окілом
точки а.
,
називають-окілом
точки а.
Геометрична
інтерпретація границі послідовності.
Якщо
а
–
границя послідовності {хn},
то для будь-якого
![]() (навіть скільки завгодно малого) можна
знайти такий номер
(навіть скільки завгодно малого) можна
знайти такий номер![]() ,
що при
,
що при![]() всі
члени послідовності попадуть в -окіл
точки а.
Інакше кажучи, для будь-якого околу з
центром в точці а,
навіть скільки завгодно малого радіусу
,
знайдеться таке значення хn,
що точки, що зображають ці значення, і
всі подальші значення послідовності
{хn},
потраплять в цей окіл (рис.3.1). Таким
чином, зовні -околу
точки а
може
лежати лише скінчене число членів
послідовності {хn}.
всі
члени послідовності попадуть в -окіл
точки а.
Інакше кажучи, для будь-якого околу з
центром в точці а,
навіть скільки завгодно малого радіусу
,
знайдеться таке значення хn,
що точки, що зображають ці значення, і
всі подальші значення послідовності
{хn},
потраплять в цей окіл (рис.3.1). Таким
чином, зовні -околу
точки а
може
лежати лише скінчене число членів
послідовності {хn}.
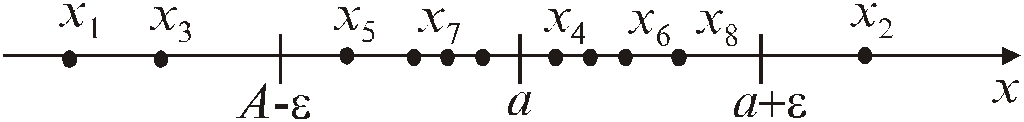
Рисунок 3.1 – Геометрична інтерпретація границі послідовності
|
|
Послідовність називають збіжною, якщо вона має границю, якщо послідовність границі не має, то вона називається розбіжною. |
Послідовність може прямувати до своєї границі різними способами:
залишаючись менше своєї границі;
залишаючись більше своєї границі;
коливаючись біля своєї границі.
|
|
Числову
послідовність називають зростаючою,
якщо кожен наступний член послідовності
більше попереднього, тобто
|
Приклади
зростаючих послідовностей:
![]() ,
,![]() .
.
|
|
Числову
послідовність називають спадаючою,
якщо кожен наступний член послідовності
менше попереднього, тобто
|
Приклади
спадаючих послідовностей:
![]() ,
,![]() .
.
|
|
Монотонними послідовностями називають зростаючі і спадаючі послідовності. |
|
|
Послідовність
називають обмеженою,
якщо існує число
|
Приклади
обмежених послідовностей:
![]() ,
,![]() ,
,![]() ;
необмежених послідовностей:
;
необмежених послідовностей:![]() ,
,![]() ,
,![]() .
.
