
- •Міністерство освіти і науки,
- •Правила оформлення контрольної роботи
- •1. Елементи лінійної алгебри
- •1.1. Матриці та дії над ними
- •Дії над матрицями
- •Основні властивості множення матриці на число
- •Основні властивості додавання та віднімання матриць
- •Основні властивості множення матриць
- •Основні властивості транспонування матриці
- •1.2. Визначники та способи їх обчислення
- •Основні властивості визначників
- •Алгоритм обчислення оберненої матриці
- •Властивості обертання невироджених матриць
- •1.3. Системи лінійних рівнянь
- •Елементарні перетворення системи лінійних рівнянь
- •Метод Крамера
- •Метод оберненої матриці
- •Метод Гаусса
- •Алгоритм прямого ходу методу Гаусса
- •2. Елементи аналітичної геометрії
- •2.1. Векторна алгебра
- •Дії над векторами
- •Властивості лінійних операцій над векторами
- •Основні властивості проекцій
- •Дії над векторами в координатній формі
- •Скалярний добуток векторів
- •Основні властивості скалярного добутку векторів
- •Векторний добуток векторів
- •Основні властивості векторного добутку векторів
- •Мішаний добуток векторів
- •Основні властивості мішаного добутку векторів
- •2.2. Пряма на площині
- •Умови взаємного розташування на площині точок і прямих
- •Контрольні питання зі змістового модуля I
- •3. Границя числової послідовності та функції. ОСновні пОняття
- •3.1. Функціональна залежність. Огляд основних елементарних функцій
- •3.2. Границя послідовності та її властивості
- •Основні теореми про послідовності, що збігаються
- •3.3. Нескінченно малі та нескінченно великі послідовності
- •Властивості нескінченно малих послідовностей
- •Властивості нескінченно великих послідовностей
- •Зв’язок між нескінченно великими і нескінченно малими послідовностями
- •3.4. Границя функції та її властивості
- •Односторонні границі функції
- •4. Обчислення границь
- •4.1. Методи розкриття невизначеностей
- •4.2. Визначні границі
- •4.3. Порівняння нескінченно малих функцій
- •Основні еквівалентності при
- •5. Неперервність функції
- •5.1. Неперервність функції в точці і на відрізку
- •Властивості функцій, які неперервні в точці
- •Властивості функцій, що неперервні на відрізку
- •5.2. Класифікація точок розриву
- •Контрольні питання зі змістового модуля II
- •6. Похідна функції однієї змінної
- •6.1. Диференційованість функції однієї змінної. Правила обчислення похідних
- •Правило знаходження похідної
- •Основні властивості похідної
- •6.2. Таблиця похідних основних елементарних функцій. Похідні вищих порядків
- •3 (Куб), ,,,.
- •6.3. Похідні функцій, заданих у параметричній, неявній формах, логарифмічне диференціювання
- •6.4. Диференціал функції однієї змінної
- •7. Диференційованість функції багатьох змінних
- •7.1. Частинні похідні та повний диференціал
- •Повний диференціал першого порядку
- •7.2. Похідна неявної, складної функції. Похідна за напрямом
- •Контрольні питання зі змістового модуля III
Умови взаємного розташування на площині точок і прямих
Умова перпендикулярності двох прямих:
|
|
Якщо
|
|
|
Якщо
перпендикулярні прямі
|
|
|
Якщо
прямі
|
Умова паралельності двох прямих:
|
|
Якщо
|
|
|
Якщо
паралельні прямі
|
|
|
Якщо
прямі
|
|
|
Якщо
виконується відношення
|
Відстань
між двома точками
![]() і
і![]() на площині визначається формулою:
на площині визначається формулою:
![]() .
(2.23)
.
(2.23)
Відстань
між точкою
![]() і прямою
і прямою![]() характеризується відношенням:
характеризується відношенням:
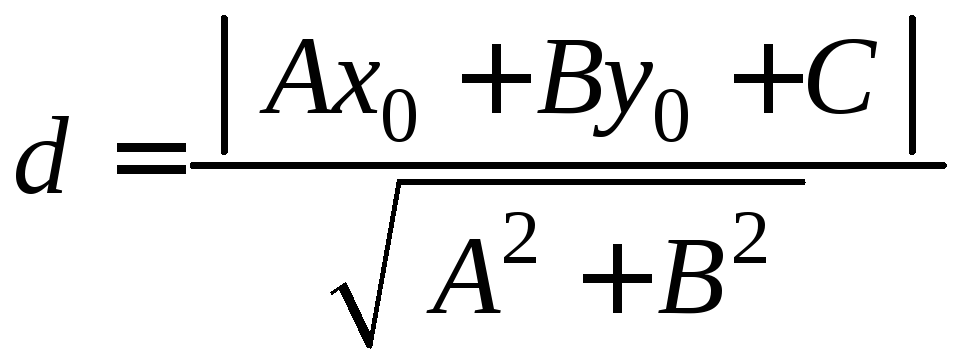 .
(2.24)
.
(2.24)
Формули
ділення відрізку
![]() у відношенні
у відношенні :
:
 ,
,
 .
(2.25)
.
(2.25)
|
Приклад 2.9. |
Обчислити
відстань від точки
|
Розв’язання.
Для
прямої l1
кутовий коефіцієнт
![]() .
З умови перпендикулярності прямих
.
З умови перпендикулярності прямих![]() одержимо
одержимо![]() .
Згідно формули (2.17) рівняння прямої
.
Згідно формули (2.17) рівняння прямої![]() ,
що проходить через задану точку
,
що проходить через задану точку![]() в заданому напрямку, що визначається
кутовим коефіцієнтом
в заданому напрямку, що визначається
кутовим коефіцієнтом![]() ,
маємо
,
маємо![]() .
Тоді
.
Тоді![]() .
.
Відстань
від точки
![]() до
до![]() дорівнює:
дорівнює:
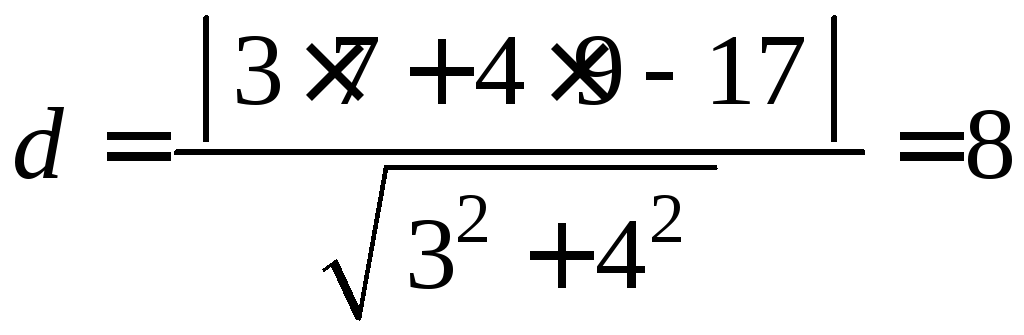 .
.
|
Приклад 2.10. |
Точка
|
Розв’язання.
За
формулами (2.25) знайдемо координати точки
![]() :
:
![]() .
.
Кутовий
коефіцієнт прямої, що треба побудувати
![]() .
Тоді за формулою (2.17) запишемо рівняння
прямої, що проходить через задану точку
.
Тоді за формулою (2.17) запишемо рівняння
прямої, що проходить через задану точку![]() у заданому напрямку
у заданому напрямку![]() :
:
![]() ,
або
,
або
![]() .
.
|
Приклад 2.11. |
За
координатами вершин
|
Розв’язання.
а) Знайдемо
рівняння
лінії, що проходить через точки
![]() і
і![]() :
:![]() ,
або
,
або
![]() ,
тобто
,
тобто![]() .
Таким чином, загальне рівняння
.
Таким чином, загальне рівняння![]() :
:
![]() .
.
б) Запишемо
спочатку рівняння
![]() з кутовим коефіцієнтом:
з кутовим коефіцієнтом:
![]() .
Таким чином,
.
Таким чином,
![]() ‑кутовий
коефіцієнт прямої
‑кутовий
коефіцієнт прямої
![]() .
Пряма
.
Пряма![]() ,
значить кутовий коефіцієнт прямої
,
значить кутовий коефіцієнт прямої![]() дорівнює
дорівнює![]() .
Користуючись рівнянням прямої (2.17), яка
проходить через точку
.
Користуючись рівнянням прямої (2.17), яка
проходить через точку
![]() в
заданому напрямку, маємо рівняння
в
заданому напрямку, маємо рівняння
![]() :
:
![]() ,
або
,
або
![]() ,
,
![]() ,
,![]() .
.
в) Довжина
висоти
![]() ‑
це відстань точки
‑
це відстань точки![]() до прямої
до прямої![]() .
Значить, за формулою (2.24)
.
Значить, за формулою (2.24)
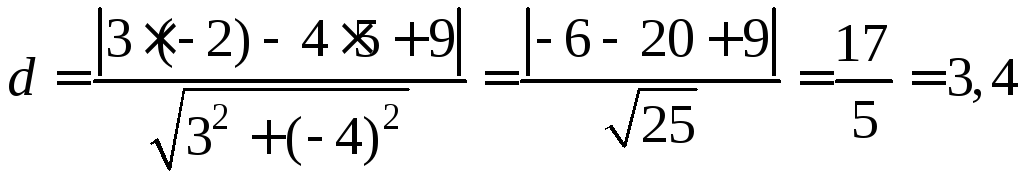 (од.)
(од.)
Контрольні питання зі змістового модуля I
|
1.1. |
Дати означення матриці, її розмірності, нульової матриці, квадратної матриці, діагональної матриці, одиничної матриці. |
|
1.2. |
Як визначають головну і допоміжну діагоналі матриці? |
|
1.3. |
Назвати основні дії над матрицями та їх властивості. |
|
1.4. |
Яка умова узгодженості матриць? |
|
1.5. |
Для
яких матриць
|
|
1.6. |
Сформулювати правило знаходження добутку двох матриць. |
|
1.7. |
Чи
повинні мати однакову розмірність
матриці
|
|
1.8. |
Сформулювати правила обчислення визначника другого і третього порядку. |
|
1.9. |
Дати означення мінору та алгебраїчного доповнення. |
|
1.10. |
Сформулювати теорему Лапласа. |
|
1.11. |
Назвати основні властивості визначників та провести ілюстрацію їх доведення на прикладі визначника другого порядку. |
|
1.12. |
Які матриці називають виродженими? |
|
1.13. |
Описати правила визначення оберненої матриці. |
|
1.14. |
Дати означення рангу матриці. |
|
1.15. |
Дати означення системи лінійних алгебраїчних рівнянь та її розв’язку. |
|
1.16. |
Описати метод оберненої матриці та метод Крамера розв’язання систем лінійних рівнянь. |
|
1.17. |
Навести алгоритм методу Гаусса. |
|
2.1. |
Дати означення вектору, його координат, модуля вектору, проекції вектора на вісь. |
|
2.2. |
Які операції можна виконувати над векторами? |
|
2.3. |
Сформулювати означення скалярного добутку двох векторів та його властивостей. |
|
2.4. |
Сформулювати умову ортогональності двох векторів. |
|
2.5. |
Сформулювати означення векторного добутку двох векторів та його властивостей. |
|
2.6. |
Сформулювати умову колінеарності двох векторів. |
|
2.7. |
Дати означення мішаного добутку трьох векторів, його властивостей та геометричного змісту. |
|
2.8. |
Сформулювати умову компланарності трьох векторів. |
|
2.9. |
Що таке пряма лінія на площині? Навести загальне рівняння прямої на площині. Який вектор називають нормальним вектором прямої? |
|
2.10. |
Який
геометричний зміст мають коефіцієнти
|
|
2.11. |
Навести рівняння прямої, що проходить через задану точку в заданому напрямку. |
|
2.12. |
Навести рівняння прямої у відрізках на осях та рівняння прямої, що проходить через дві задані точки. |
|
2.13. |
Як знайти кут між двома прямими на площині? Навести формули. |
|
2.14. |
Навести умови перпендикулярності двох прямих на площині. |
|
2.15. |
Навести умови паралельності двох прямих на площині. |
|
2.16. |
Як знайти відстань між двома точками та між точкою та прямою на площині? Навести формули. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗМІСТОВИЙ МОДУЛЬ 2
Границі Функції

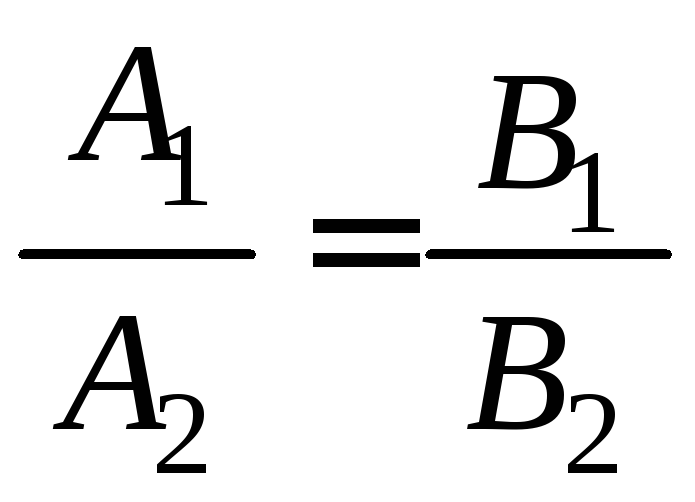 .
.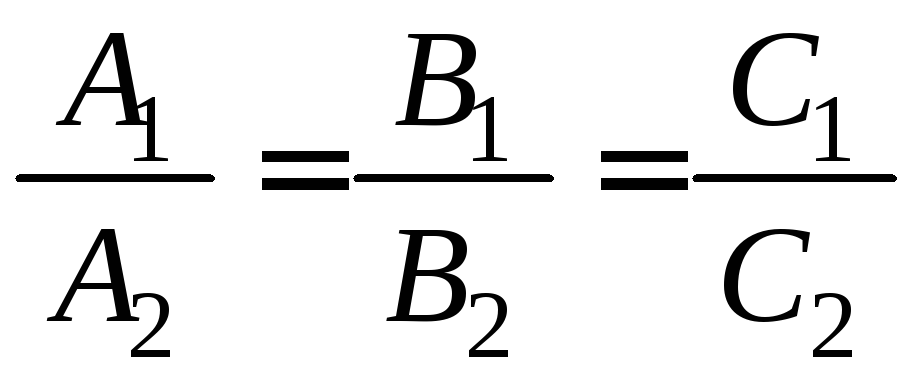 ,
то прямі
,
то прямі