Основні властивості векторного добутку векторів

1)	;
2)	;
3)	;
4)	векторний добуток двох ненульових векторів дорівнює нулю тоді і тільки тоді, коли вектори колінеарні: ;
5)	.

Приклад 2.5.

Знайти синус кута між векторами i, а також площу паралелограма, побудованого на цих векторах.

Розв’язання. За формулою (2.11) обчислимо векторний добуток :

.

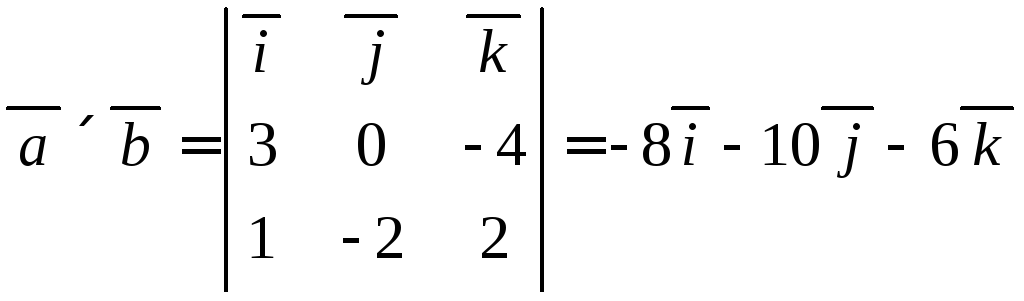Довжину векторів ,і знайдемо згідно (2.3):

, ,.

З формули (2.11) маємо: .

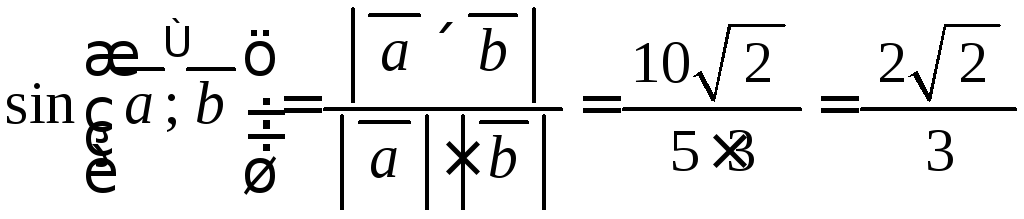Відповідно до означення векторного добутку площа паралелограма, побудованого на векторах і дорівнює.

Мішаний добуток векторів

Мішаним добутком векторів , іназивається скалярний добуток векторана вектор.

Якщо ,і, то мішаний добуток векторів у координатній формі має вигляд:

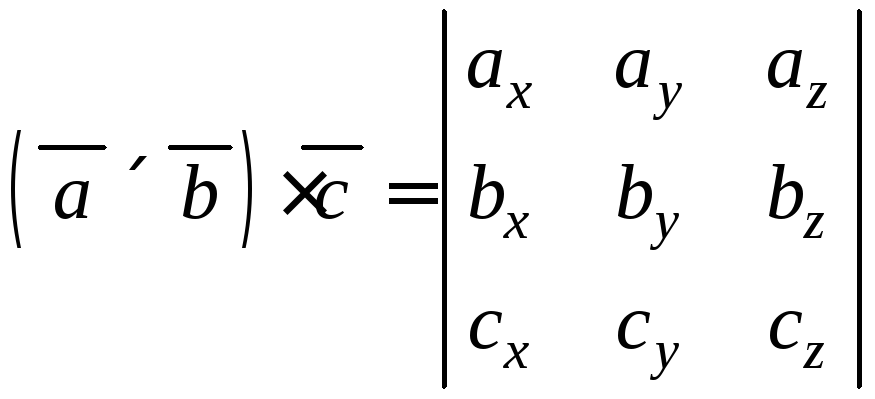. (2.12)

Основні властивості мішаного добутку векторів

1)	;
2)	мішаний добуток трьох ненульових векторів дорівнює нулю тоді і тільки тоді, коли вони компланарні;
3)	модуль мішаного добутку дорівнює об’єму паралелепіпеда, що побудовано на даних векторах;

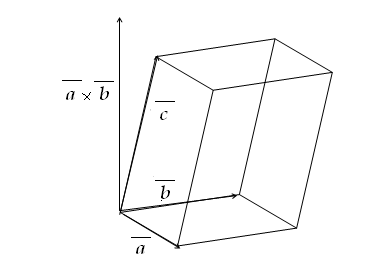
Рисунок 2.11  Паралелепіпед, що побудовано на векторах , і.

Зауваження

Об’єм піраміди, яку побудовано на векторах ,і, дорівнює модулю змішаного добутку цих векторів, що поділено на 6.

Приклад 2.6.

Довести, що точки ,,ілежать в одній площині.

Розв’язання. Знайдемо координати векторів, що виходять з точки :,,.

Доведемо, що ці вектори є компланарними, тобто належать одній площині. Для цього обчислимо мішаний добуток одержаних векторів:

.

Згідно другої властивості мішаного добутку вектори ,іє компланарними, отже точки,,ілежать в одній площині.

Приклад 2.7.

Знайти об’єм піраміди і довжину висоти, яку опущено на грань, якщо вершини,,імають наступні координати:,,,.

Розв’язання. Знайдемо координати векторів, що виходять з вершини :,,.

Рисунок 2.12  Піраміда, що побудована на векторах ,,.

Обчислимо мішаний добуток одержаних векторів: 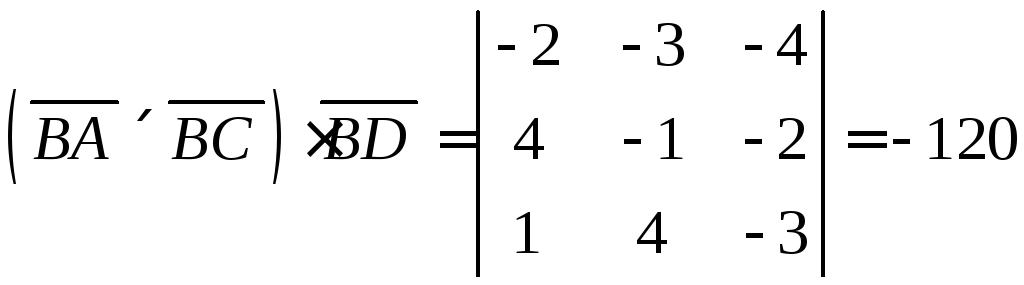. Отже, об’єм піраміди:

.

Для знаходження висоти обчислимо спочатку площу грані, як модуля векторного добутку векторіві:

,

.

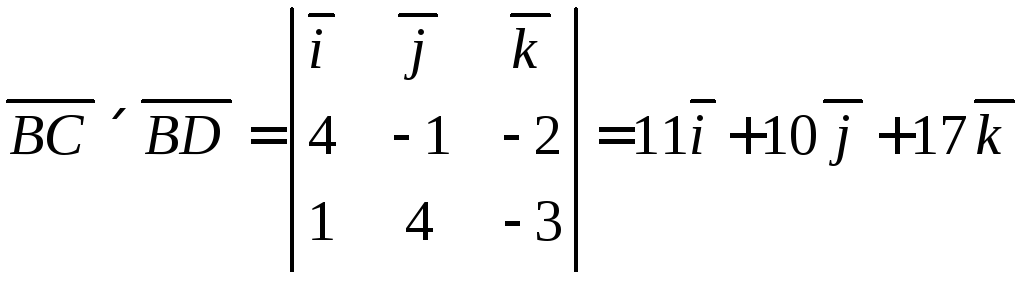Отже, площа трикутника дорівнює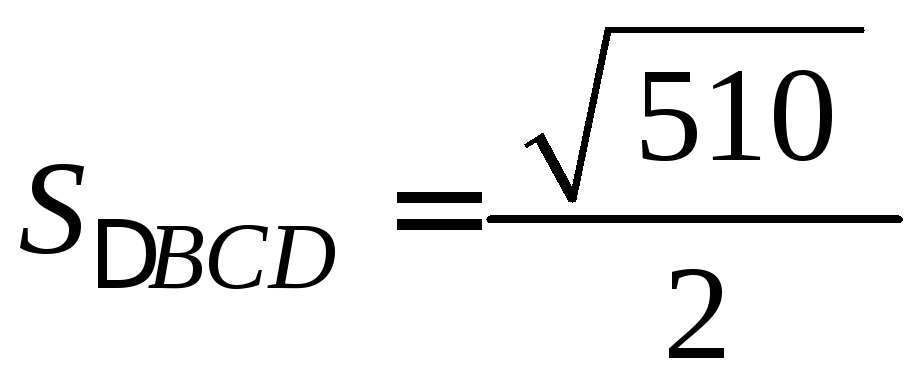. Тоді з відомої формулимаємо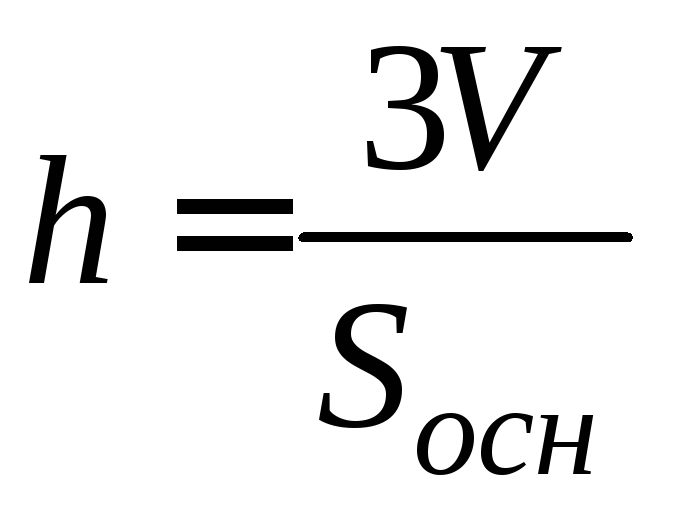, звідки одержимо.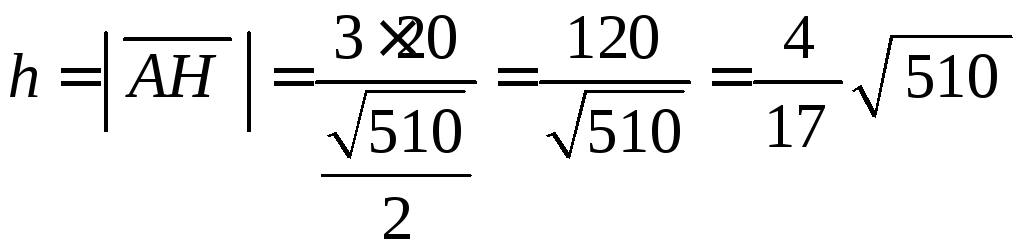

2.2. Пряма на площині

Розглянемо найпростішу лінію на площині – пряму. Існують різні форми запису рівняння прямої лінії на площині.

Нехай − пряма лінія на координатній площині.,− фіксована точка на, ненульовий вектор , перпендикулярний до. Його називаютьнормальним вектором прямої.

Завдання точки і вектораповністю визначає прямуі таким чином можна задати будь-яку пряму лінію на площині. Довільна точкабуде належати прямійтоді і тільки тоді, коли векториібудуть взаємно перпендикулярними (рис. 2.13).

Рисунок 2.13  Завдання прямої на площині.

Для цього, в свою чергу, необхідно і достатньо, щоб скалярний добуток цих векторів дорівнював нулю

. (2.13)

Оскільки , то можна виразити скалярний добутокчерез координати множників:

. (2.14)

Рівняння (2.14) є рівнянням прямої на площині в координатній формі. Відношення (2.14) називають ще рівнянням прямої, що проходить через задану точку в заданому напрямку.

Відношення , (2.15) де , визначаєзагальне рівняння прямої на площині.

Термін «загальне» пояснюють тим, що довільна пряма на площині може бути заданою рівнянням першого степеня відносно змінних і(при цьому коефіцієнтиіне дорівнюють нулю одночасно, бо нормальний вектор прямої не нульовий).

Пряма лінія на площині – це геометричне місце точок площини, координати яких задовольняють рівнянню першої степені відносно і.

Будь-яка пряма на площині визначається рівнянням першого ступеня відносно і. Будь-якому рівнянню першого ступеня відносноівідповідає пряма лінія в декартовій системі координат.

Відмітимо характерні випадки загального рівняння прямої, коли деякі коефіцієнти дорівнюють нулю.

1)	Нехай , тоді рівняння (2.15) має вигляд: де . Всі точки прямої мають однакову ординату, тобто пряма паралельна осі абсцис.
2)	Нехай , тоді. Пряма співпадає з віссю.
3)	Нехай , тоді рівняння (2.15) має вигляд: , де . Всі точки прямої мають однакову абсцису, тому пряма паралельна осі ординат.
4)	Нехай , тоді. Пряма співпадає з віссю.
5)	Нехай , тоді пряманезалежно від значеньіпроходить через початок координат т..

Нехай . Розв’яжемо рівняння (2.15) відносно змінної:

,

або

. (2.16)

Рівняння (2.16) називають рівнянням прямої з кутовим коефіцієнтом і початковою ординатою.

Зміст коефіцієнтів у (2.16):

	‑кутовий коефіцієнт прямої, − кут нахилу прямої до.
	−ордината точки перетину прямої з віссю , початкова ордината прямої (рис. 2.14).

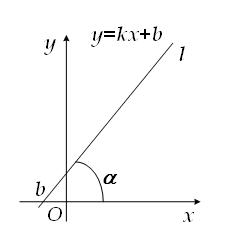
Рисунок 2.14  Пряма з кутовим коефіцієнтом

Рівняння (2.17) називають рівнянням прямої, яка проходить через задану точку в заданому напрямку.

При фіксованій точці і різних значенняхце рівняння дає множину прямих, яку називаютьпучком прямих з центром в точці . Але тільки одну пряму з всіх, які проходять через, а саме пряму, перпендикулярну до осі абсцис, не можна визначити таким рівнянням. Її рівнянням буде.

Нехай потрібно скласти рівняння прямої, що проходить через дві задані точки і(вважаємо, що,).

Знайдемо кутовий коефіцієнт цієї прямої, для чого обчислимо тангенс кута, який утворює відрізок з віссю(рис.2.15)

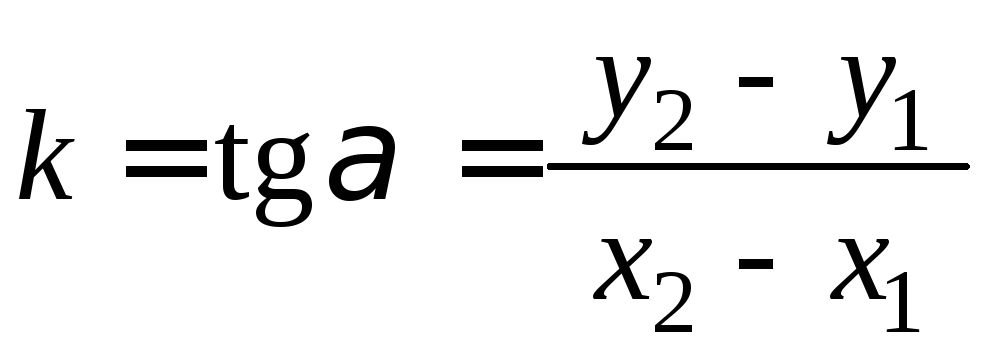. (2.18)

Рисунок 2.15  Рівняння прямої, що проходить через дві задані точки

Підставимо вираз (2.18) у відношення (2.17) і запишемо останнє рівняння в симетричній формі:

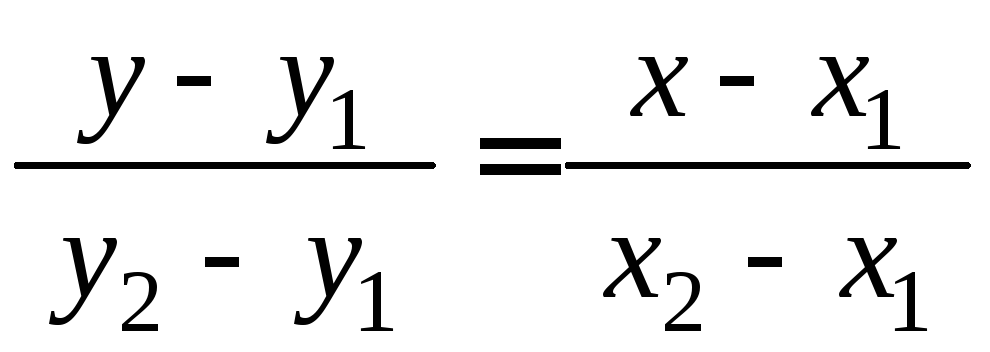. (2.19)

Рівняння (2.19) називають рівнянням прямої, яка проходить через дві задані точки.

Нехай пряма відсікає на осі абсцис відрізок, а на осі ординат – відрізок(рис. 2.16), тоді шукана пряма проходить через точкиі.

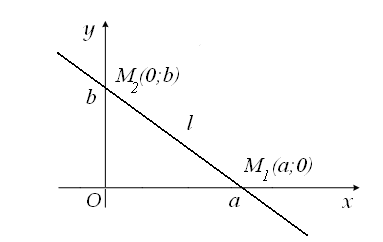
Рисунок 2.16.  Рівняння прямої у відрізках на осях

Підставимо координати цих точок у рівняння (2.19) і одержимо:

. (2.20)

Рівняння (2.20) називають рівнянням прямої у відрізках на осях. Тут величини і− це довжини, які взяли з належними знаками, відрізків, що прямавідсікає від осей координат.

Нехай прямі ізадано рівняннями:

, .

Тоді вектор буде нормальним до, а векторбуде нормальним до.

Якщо прямі інепаралельні, то кутміж нормальними векторамиідорівнює одному з кутів, створених прямимиі.

З формули (2.6) маємо:

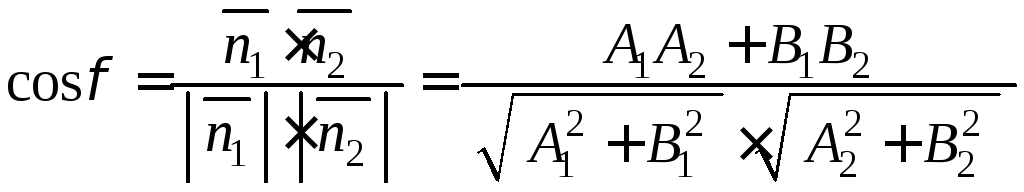. (2.21)

Якщо , тоабо.

Часто зручнішою виявляється формула, яка пов’язує тангенс кута між двома прямими через їхні коефіцієнти і:

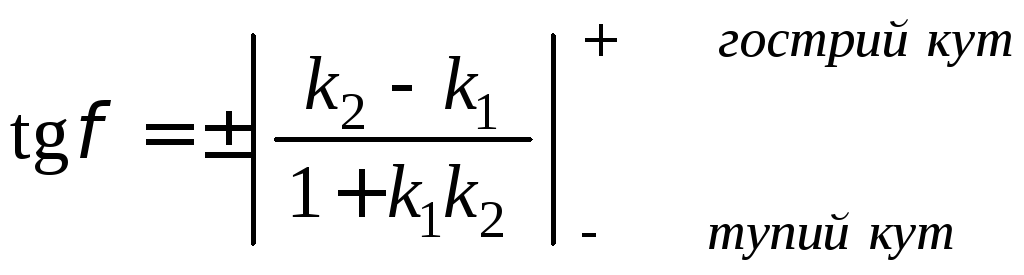(2.22)

Приклад 2.8.

Знайти кут між прямими і.

Розв’язання. За формулою (2.21) одержимо:

.

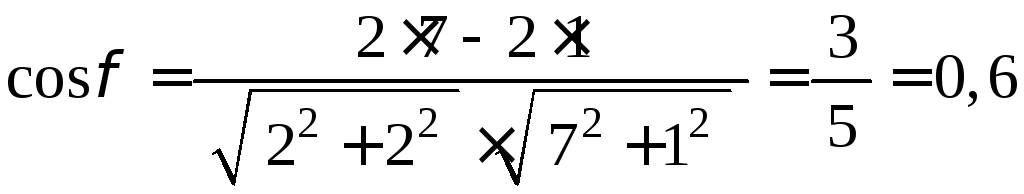Отже, .