
- •Міністерство освіти і науки,
- •Правила оформлення контрольної роботи
- •1. Елементи лінійної алгебри
- •1.1. Матриці та дії над ними
- •Дії над матрицями
- •Основні властивості множення матриці на число
- •Основні властивості додавання та віднімання матриць
- •Основні властивості множення матриць
- •Основні властивості транспонування матриці
- •1.2. Визначники та способи їх обчислення
- •Основні властивості визначників
- •Алгоритм обчислення оберненої матриці
- •Властивості обертання невироджених матриць
- •1.3. Системи лінійних рівнянь
- •Елементарні перетворення системи лінійних рівнянь
- •Метод Крамера
- •Метод оберненої матриці
- •Метод Гаусса
- •Алгоритм прямого ходу методу Гаусса
- •2. Елементи аналітичної геометрії
- •2.1. Векторна алгебра
- •Дії над векторами
- •Властивості лінійних операцій над векторами
- •Основні властивості проекцій
- •Дії над векторами в координатній формі
- •Скалярний добуток векторів
- •Основні властивості скалярного добутку векторів
- •Векторний добуток векторів
- •Основні властивості векторного добутку векторів
- •Мішаний добуток векторів
- •Основні властивості мішаного добутку векторів
- •2.2. Пряма на площині
- •Умови взаємного розташування на площині точок і прямих
- •Контрольні питання зі змістового модуля I
- •3. Границя числової послідовності та функції. ОСновні пОняття
- •3.1. Функціональна залежність. Огляд основних елементарних функцій
- •3.2. Границя послідовності та її властивості
- •Основні теореми про послідовності, що збігаються
- •3.3. Нескінченно малі та нескінченно великі послідовності
- •Властивості нескінченно малих послідовностей
- •Властивості нескінченно великих послідовностей
- •Зв’язок між нескінченно великими і нескінченно малими послідовностями
- •3.4. Границя функції та її властивості
- •Односторонні границі функції
- •4. Обчислення границь
- •4.1. Методи розкриття невизначеностей
- •4.2. Визначні границі
- •4.3. Порівняння нескінченно малих функцій
- •Основні еквівалентності при
- •5. Неперервність функції
- •5.1. Неперервність функції в точці і на відрізку
- •Властивості функцій, які неперервні в точці
- •Властивості функцій, що неперервні на відрізку
- •5.2. Класифікація точок розриву
- •Контрольні питання зі змістового модуля II
- •6. Похідна функції однієї змінної
- •6.1. Диференційованість функції однієї змінної. Правила обчислення похідних
- •Правило знаходження похідної
- •Основні властивості похідної
- •6.2. Таблиця похідних основних елементарних функцій. Похідні вищих порядків
- •3 (Куб), ,,,.
- •6.3. Похідні функцій, заданих у параметричній, неявній формах, логарифмічне диференціювання
- •6.4. Диференціал функції однієї змінної
- •7. Диференційованість функції багатьох змінних
- •7.1. Частинні похідні та повний диференціал
- •Повний диференціал першого порядку
- •7.2. Похідна неявної, складної функції. Похідна за напрямом
- •Контрольні питання зі змістового модуля III
Дії над векторами
|
1. |
Сума векторів |
|
|
Сумою
двох
векторів
|
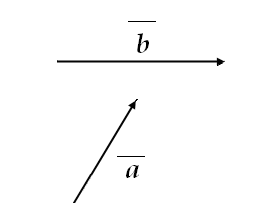
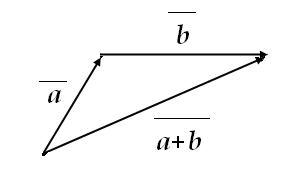
Рисунок
2.5
Сума векторів
![]() і
і![]()
Для того, щоб додати декілька векторів, слід побудувати з них ламану, щоб наступний вектор виходив з попереднього, а потім з’єднати початок ламаної з її кінцем.
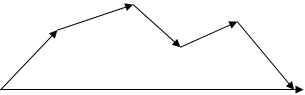
Рисунок 2.6 Додавання векторів
|
2. |
Різниця векторів |
|
|
Різницею
двох
векторів
|

Рисунок 2.7 Різниця векторів.
![]() ,
тобто
,
тобто
![]() .
.
|
|
Вектор,
який в сумі з вектором
|
Протилежний
вектор отримують зміною напрямку вектора
![]() .
.
Різницю
векторів
![]() і
і![]() можна подати у вигляді
можна подати у вигляді![]() .
.
Суму двох неколінеарних векторів можна будувати як діагональ паралелограму, що побудовано на даних векторах, приведених до спільного початку, і що виходить з цього спільного початку.
Інша
діагональ паралелограму, що йде з кінця
![]() в кінець
в кінець![]() ,
є різницею
,
є різницею![]() і
і![]() .
.
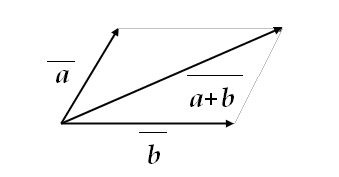

Рисунок
2.8
Сума та різниця векторів
![]() і
і![]()
|
3. |
Добуток числа на вектор |
|
|
Добутком
числа
є
колінеарним вектору
|
Властивості лінійних операцій над векторами
|
1) |
|
|
2) |
|
|
3) |
|
|
4) |
|
|
5) |
|
|
6) |
|
|
7) |
|
|
8) |
|
|
9) |
|
|
|
Проекцією
вектора
Величиною
проекції
називають довжину вектору проекції
|
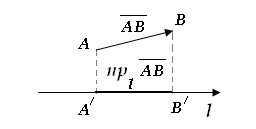
Рисунок 2.9 Проекція вектора на вісь.
Основні властивості проекцій
|
1) |
Проекції
рівних векторів на вісь співпадають:
якщо
|
|
2) |
Проекція
суми векторів на вісь дорівнює сумі
проекцій доданків на цю вісь:
|
|
3) |
Проекція
добутку вектора на число дорівнює
добутку проекції цього вектора на
число:
|
|
4) |
Величина
проекції вектора на вісь дорівнює
добутку модуля вектора на косинус
кута
|
|
5) |
|
|
6) |
|
|
7) |
|
|
8) |
|
|
9) |
|
Позначимо
через
![]() ,
,![]() ,
,![]() орти координатних осей (вектори одиничної
довжини, що розташовані відповідно на
осях
орти координатних осей (вектори одиничної
довжини, що розташовані відповідно на
осях![]() ,
,![]() ,
,![]() і напрямок яких співпадає з напрямком
осей).
і напрямок яких співпадає з напрямком
осей).
|
|
Координатами
вектора
|
Нехай
![]()
вектор, що розглядається,
вектор, що розглядається,
![]()
проекції вектору
проекції вектору
![]() на координатні вісі:
на координатні вісі:
![]() ,
,
![]() ,
,![]() .
.
Тоді
можна записати формулу розкладення
вектору
![]() за координатними осями:
за координатними осями:
![]() .
(2.1)
.
(2.1)
Після
вибору в просторі декартової системи
координат вектор
![]() і трійка його координат
і трійка його координат![]() взаємно визначають один одне. Тому
розкладення вектору зручно записувати
у вигляді
взаємно визначають один одне. Тому
розкладення вектору зручно записувати
у вигляді![]() .
Це запис вектора в координатній формі.
.
Це запис вектора в координатній формі.
Якщо
![]()
координати точки
координати точки
![]() ,
,![]()
координати точки
координати точки
![]() ,
то координати вектору
,
то координати вектору![]() дорівнюють різницям відповідних
координат його кінця
дорівнюють різницям відповідних
координат його кінця![]() і початку
і початку![]() :
:
![]() .
(2.2)
.
(2.2)
