4. Ряды
Удобным и полезным инструментом в математическом анализе являются бесконечные ряды. Теория рядов представляет собой сравнительно небольшой и несложный материал, тем не менее, она служит опорой для многих прикладных наук и имеет многочисленные конкретные приложения.
4.1. Числовые ряды |
|
|
|
4.1.1. Понятие числового ряда и его сходимости |
|
||
Пусть дана |
бесконечная |
последовательность |
чисел |
a1, a2 , a3 ,..., an ,... . |
|
|
|
Определение 4.1. Числовым рядом называется выражение |
|||
|
|
∞ |
|
a1 + a2 +...+ an +... = ∑an , |
(4.1) |
||
|
|
n=1 |
|
где числа a1, a2 , a3 ,..., an ,... называются членами ряда, а an |
= f (n) |
||
называется общим членом ряда. |
|
|
|
Для корректного определения суммы бесконечного ряда опять |
|||
воспользуемся операцией предельного перехода. |
|
||
Определение 4.2. Частичной n -ой суммой ряда |
(4.1) |
||
называется сумма Sn |
его первых n |
членов: Sn = a1 +a2 +...+ an . |
|
Образуем теперь последовательность S1, S2 ,...Sn ,..., |
состоящую |
||||||||||||||||
из частичных сумм ряда (4.1). |
|
|
|
|
|
|
|
|
|||||||||
Определение 4.3. Если существует конечный предел S |
|||||||||||||||||
последовательности |
частичных |
сумм |
S = lim Sn , |
то |
ряд (4.1) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n→∞ |
|
|
|
называется сходящимся, а число S ― суммой ряда и записывается |
|||||||||||||||||
этот факт как S = |
∞ a |
n |
. |
Если |
lim S |
n |
не существует или равен |
||||||||||
|
∑ |
|
|
|
|
|
n→∞ |
|
|
|
|
|
|||||
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
бесконечности, то ряд (4.1) называется расходящимся. |
|
||||||||||||||||
Пример 4.1. Исследовать на сходимость ряд |
|
|
|||||||||||||||
|
1 |
|
+ |
1 |
|
+ |
1 |
|
+...+ |
|
|
1 |
|
+... |
|
||
|
2 5 |
|
|
8 11 |
(3n −1)(3n + 2) |
|
|||||||||||
|
|
5 8 |
|
|
|
|
|||||||||||
по определению, и, если ряд сходится, то найти его сумму.
95
Решение. Представим общий член ряда an |
= |
|
|
1 |
|
|
в |
||||||||||||
(3n − |
1)(3n |
+ 2) |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
виде двух слагаемых |
1 |
|
= |
|
a |
|
|
+ |
|
|
b |
|
и найдем |
||||||
(3n −1)(3n + 2) |
3n −1 |
|
3n + 2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
числа a и b методом неопределенных коэффициентов: |
|
|
|
|
|||||||||||||||
1 |
|
= a(3n +2) +b(3n −1) |
= |
n(3a +3b) + 2a −b . |
|
||||||||||||||
|
(3n −1)(3n +2) |
|
|||||||||||||||||
|
|
(3n −1)(3n + 2) |
|
|
|
|
(3n −1)(3n + 2) |
|
|
|
|||||||||
Значит, для |
любых |
чисел |
n N |
должно |
|
быть |
выполнено |
||||||||||||
равенство n(3a +3b) + 2a −b =1. |
Это возможно, |
|
в том и только в |
|
|||||||||||||||
том случае, когда коэффициенты при n и n0 в левой и правой частях последнего равенства совпадают:
3a +3b = 0, |
|
|
|
|
|
|
|
|
b = −a, |
|
|
|
b = −1 3, |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2a −b =1, |
|
|
|
|
|
|
|
|
|
|
2a + a =1, |
|
|
|
a =1 3. |
||||||||
Значит, |
an |
= |
|
|
1 3 |
− |
|
1 3 |
, |
а тогда |
|
|
|
|
|
||||||||
|
3n −1 |
3n + 2 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1 |
+ |
1 |
|
+ |
|
|
1 |
|
|
+...+ |
|
1 |
|
= (1 3 |
− |
1 3) +(1 3 |
−1 3) + |
|||||
|
2 5 |
|
|
|
8 11 |
(3n −1)(3n + 2) |
|||||||||||||||||
|
|
5 8 |
|
|
|
|
|
2 |
|
5 |
5 |
8 |
|||||||||||
+183 +1113) +...+(31n
−31 − 3n1
+32).
Вэтой сумме все слагаемые, кроме первого и последнего, взаимно уничтожаются. Следовательно, Sn = 16 − 3n1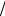
+32 .
Находим теперь
lim S |
n |
= lim( |
1 |
− |
1 3 |
) = |
1 |
− |
1 |
lim |
1 |
= |
1 |
− |
1 |
0 = |
1 . |
|
6 |
3n + 2 |
6 |
3 |
3n + 2 |
6 |
3 |
||||||||||||
n→∞ |
n→∞ |
|
|
|
n→∞ |
|
|
|
6 |
Итак, данный ряд сходится и его сумма равна S = 16 .
96
Ряд
|
|
∞ |
|
a + aq + aq2 |
+...+ aqn−1 |
+... = ∑aqn−1, |
a ≠ 0 , (4.2) |
n=1
составленный из членов геометрической прогрессии со знаменателем q , называется геометрическим рядом. Если q <1,
то ряд (4.2) сходится и его сумма равна S = |
a |
; если |
|
q |
|
≥1, то |
|
|
|
||||||
1−q |
|||||||
|
|
|
|
|
|
ряд (4.2) расходится.
Обобщенным гармоническим рядом называется ряд вида
∞ |
1 |
|
|
|
|
|
|
|
|
|
|
∑ |
. Этот ряд сходится, |
если p >1 |
и расходится, если p ≤1. В |
||||||||
p |
|||||||||||
n=1 |
n |
|
|
|
|
|
|
|
|
||
частности, |
ряд |
1+ 1 |
+ 1 +...+ |
1 |
∞ |
1 |
, |
называемый |
|||
+... = ∑ |
|||||||||||
гармоническим рядом, |
2 |
3 |
n |
n=1 |
n |
|
|
||||
расходится. |
|
|
|
|
|
||||||
4.1.2. Простейшие свойства сходящихся рядов
Определение 4.4. Если в ряде (4.1) отбросить первые n членов, то получится ряд rn , называемый остатком ряда (4.1) после n -го
члена:
∞ |
|
rn = an+1 + an+2 +...+ an+k +... = ∑ak |
(4.3) |
k =n+1
Теорема 4.1. Если ряд (4.1) сходится, то сходится и любой его остаток и, наоборот, если остаток (4.3) сходится, то сходится и ряд (4.1).
Определение 4.5. Произведением ряда (4.1) на постоянное число c называется ряд
∞ |
|
ca1 +ca2 +...+can +... = ∑can |
(4.4) |
n=1
Теорема 4.2. Если ряд (4.1) сходится и его сумма равна S , то и ряд (4.4) сходится и его сумма равна cS.
97
Определение |
4.6. |
|
Суммой |
(разностью) |
рядов |
||
|
∞ |
|
|
|
∞ |
|
|
a1 +a2 +...+ an +... = ∑an |
и |
b1 +b2 +...+bn +... = ∑bn |
называется |
||||
ряд |
n=1 |
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
(a1 ±b1) +(a2 ±b2 ) +...+(an ±bn ) +... = ∑(an ±bn ). |
|
||||||
|
|
|
|
|
n=1 |
|
|
|
|
|
∞ |
∞ |
|
|
|
Теорема 4.7. Если ряды ∑an |
и ∑bn сходятся и имеют суммы |
||||||
|
|
|
n=1 |
n=1 |
|
|
|
S1 и S2 , соответственно, то их сумма и разность сходятся и имеют суммы S1 ± S2 .
4.1.3. Необходимый признак сходимости ряда и его следствие
Исследование сходимости рядов является основной задачей. Как это осуществить более простым способом, чем непосредственное нахождение его суммы? Ниже приведены несколько утверждений, позволяющих делать в некоторых случаях заключение о сходимости или расходимости рядов.
Теорема 4.3 (необходимый признак сходимости). Если ряд (4.1) сходится, то общий член этого ряда стремится к нулю:
lim an = 0 .
n→∞
Следствие (достаточный признак расходимости ряда). Если
lim an ≠ 0 , то ряд (4.1) расходится.
n→∞
Пример 4.2. Исследовать на сходимость ряд ∑∞ 2n −1 . n=1 3n + 2
Решение. Находим |
lim an = lim |
2n −1 |
|
∞ |
= lim |
2 −1 n |
= |
2 |
. |
|||
|
= |
|
|
|
|
|||||||
3n + 2 |
3 |
+2 n |
3 |
|||||||||
|
n→∞ |
n→∞ |
|
∞ |
n→∞ |
|
|
|||||
Поскольку 23 ≠ 0, то на основании следствия из теоремы (4.3) данный ряд расходится.
98