
- •Оглавление
- •Введение
- •1. Дифференциальное исчисление функций многих переменных
- •1.1. Предел и непрерывность функций многих переменных
- •1.1.1. Понятие функции многих переменных
- •1.1.2. Геометрическая иллюстрация функции двух переменных
- •1.1.3. Предел функции двух переменных в точке
- •1.1.4. Непрерывность функции двух переменных
- •1.2. Дифференцируемость функции многих переменных
- •1.2.1. Частные производные
- •1.2.2. Дифференцируемые функции
- •1.2.3. Полный дифференциал функции многих переменных
- •1.2.5. Производные высших порядков
- •1.3. Экстремум функции многих переменных
- •1.3.1. Понятие экстремума. Необходимое условие экстремума
- •1.4. Метод наименьших квадратов
- •1.4.1. Понятие эмпирической формулы
- •1.4.2. Выравнивание экспериментальных данных по прямой
- •1.4.3. Выравнивание экспериментальных данных по параболе
- •1.4.4. Выравнивание экспериментальных данных по гиперболе
- •2. Интегральное исчисление
- •2.1. Неопределенный интеграл
- •2.1.1. Определение первообразной и неопределенного интеграла
- •2.1.2. Основные свойства неопределенного интеграла
- •2.1.3. Таблица основных неопределенных интегралов
- •2.1.4. Непосредственное интегрирование. Поднесение под знак дифференциала
- •2.2. Основные методы интегрирования
- •2.2.1. Замена переменной в неопределенном интеграле
- •2.2.2. Интегрирование некоторых иррациональных функций
- •2.2.3. Интегрирование тригонометрических функций
- •2.2.4. Интегрирование по частям
- •2.2.5. Интегрирование рациональных функций
- •2.3. Определенный интеграл
- •2.3.1. Определение определенного интеграла
- •2.3.2. Необходимое условие интегрируемости функций. Классы интегрируемых функций
- •2.3.3.Свойства определенного интеграла
- •2.3.5. Замена переменной в определенном интеграле
- •2.3.7. Геометрические приложения определенного интеграла
- •2.4. Несобственные интегралы
- •2.4.2. Несобственные интегралы от неограниченных функций
- •3.1. Понятие обыкновенного дифференциального уравнения n-го порядка и его решения
- •3.2. Дифференциальные уравнения первого порядка
- •3.2.1. Понятие дифференциального уравнения первого порядка и его решения. Задача Коши. Теорема Коши. Понятие общего решения
- •3.2.4. Однородные дифференциальные уравнения первого порядка
- •3.3. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •3.3.1. Постановка задачи Коши и понятие общего решения для линейного дифференциального уравнения второго порядка
- •3.3.2. Свойства решений линейных однородных уравнений
- •3.3.3. Решение однородных линейных уравнений второго порядка с постоянными коэффициентами
- •4. Ряды
- •4.1. Числовые ряды
- •4.1.1. Понятие числового ряда и его сходимости
- •4.1.2. Простейшие свойства сходящихся рядов
- •4.1.3. Необходимый признак сходимости ряда и его следствие
- •4.1.4. Достаточные признаки сходимости рядов с неотрицательными членами
- •4.1.5. Знакопеременные ряды. Абсолютная и условная сходимость
- •4.1.6. Знакочередующиеся ряды. Признак Лейбница
- •4.2. Степенные ряды
- •4.2.1. Понятие функционального ряда и его области сходимости
- •4.2.2. Степенные ряды. Теорема Абеля
- •4.2.3. Интервал, радиус и область сходимости степенного ряда
- •4.2.4. Ряды Тейлора и Маклорена. Разложение некоторых элементарных функций в степенные ряды
- •Вопросы для повторения и тренировочные задания
- •1. Функции многих переменных
- •2а. Неопределенный интеграл
- •2б. Определенный интеграл
- •3: Дифференциальные уравнения
- •4. Ряды
- •Вопросы к экзамену
- •Литература

б) ∫
в) ∫
= −
г) ∫
= ∫
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xdx |
|
|
|
|
|
|
|
|
|
|
|
2 d(x |
|
+1) |
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
= |
∫ |
|
|
|
|
|
|
= |
2 arctg(x |
|
+1) +C. |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x2 +1)2 +1 |
|
|
||||||||||||||||||||||||||||||
|
|
|
x4 +2x2 +2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
dx |
|
|
|
|
|
|
|
= ∫ (ctg x) |
−1 |
3 |
|
|
|
|
dx |
= −∫ |
(ctg x) |
−1 |
3 d(ctg x) = |
||||||||||||||||||||||
|
|
|
sin2 x3 |
|
|
|
|
|
|
|
|
|
|
|
sin2 x |
|
||||||||||||||||||||||||||||||
|
|
|
ctg x |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
(ctg x) |
−1 |
3 |
+1 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
+C |
= − |
3 ctg |
2 |
x +C. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
− |
3 +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
dx |
|
|
|
|
= ∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
= |
|
|
||||||||||
|
|
|
x2 + x −2 |
|
x |
2 |
+ |
2 x |
1 |
|
|
|
1 |
2 |
|
1 |
2 |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
+ |
2 |
|
− |
|
−2 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
3 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
d x |
+ |
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
x + 2 − 2 |
|
|
|
1 ln |
|
x −1 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
ln |
+C = |
|
+C. |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|||||||||||||||||||||
|
|
|
1 |
2 |
|
|
3 |
|
2 |
|
|
|
2 |
|
|
|
x + |
1 |
+ |
3 |
|
|
|
3 |
|
|
x + 2 |
|
||||||||||||||||||
|
x + |
|
|
|
|
− |
|
|
|
|
|
2 |
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
2.2.Основные методы интегрирования
Ксожалению, общего метода интегрирования нет, тем не ме-
нее, ниже мы укажем некоторые приемы вычисления интегралов. Сравнительно в редких случах удается дать правила для интегрирования.. Но и тогда, когда имеются эти правила, они вовсе не являются наилучшим, или наиболее экономным путем. Вычисление чаще всего может быть выполнено не единственным способом (это своеобразное искусство!). Владение операцией интегрирования (как и многими другими математическими операциями) заключается не только в знании того как можно в конце концов взять интеграл, но и в умении сделать это с наименьшей затратой времени и труда.
39
2.2.1. Замена переменной в неопределенном интеграле
Во многих случаях введение новой переменной интегрирования позволяет свести нахождение данного интеграла к нахождению табличного интеграла. Такой метод называется методом под-
становки или методом замены переменной.
Теорема 2.1. Пусть требуется найти интеграл ∫ f (ϕ(x)) ϕ′(x) dx , где подынтегральная функция непрерывна и из-
вестно, что ∫ f (t) dt = F(t) +C . Тогда
∫ f (ϕ(x)) ϕ′(x) dx = ∫ f (φ(x)) dφ(x) =F(ϕ(x)) +C.
Теорема 2.2. Пусть требуется найти ∫ f (x)dx , где f (x) −непрерывная функция. Если φ (t) −строго монотонная функция, име-
ющая |
|
непрерывную |
производную |
φ′ (t) , и |
|
при |
x =φ (t), |
|||||||||||||||||||||||||||||||||||
dx =φ (t) dt |
справедливо равенство |
f (x) = f ( φ (t)) = g(t) , |
причем |
|||||||||||||||||||||||||||||||||||||||
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ g |
(t) |
ϕ |
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
(t) dt = G(t) +C , то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ f (x)dx = G(ψ (x)) +C, |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
где ψ (x) |
– обратная функция для функции x = φ (t) . |
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
Полезно запомнить формулу: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
∫ |
|
|
f ′(x) |
|
dx = ∫ |
df (x) = ln |
|
f (x) |
|
+C |
|
|
|
|
|
|
|
(2.4) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
f (x) |
|
|
|
f (x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
С помощью этой формулы можно вычислять, например, инте- |
||||||||||||||||||||||||||||||||||||||||
гралы вида |
∫ |
|
tg x dx, |
∫ ctg x dx, |
∫ |
|
dx |
|
, |
|
a ≠ 0, |
|
а так же и дру- |
|||||||||||||||||||||||||||||
ax +b |
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos xdx |
|
|
|
|
|
|
|
|||||||||
гие |
интегралы. |
Например, |
|
|
|
∫ ctg x dx = ∫ |
= ln |
|
sin x |
|
+C; |
|||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
∫ |
|
dx |
|
|
= 1 |
∫ |
|
3dx |
= |
1 ln |
|
3x −2 |
|
+C; |
|
|
|
|
|
|
|
|
sin x |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
3x −2 |
|
3 |
|
|
3x −2 |
3 |
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
3x |
2 |
−2 |
|
|
|
(x |
3 |
|
−2x |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
∫ |
|
dx = ∫ |
|
dx |
|
= ln |
x |
|
− |
2x +1 |
+C. |
||||||||||||||||||||||||||
|
|
|
|
|
x3 −2x +1 |
x3 −2x +1 |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
40

Пример 2.4. Используя метод подстановки, найти интеграл
∫ x dx 2 x .
 1+ln
1+ln
Решение. Выполним подстановку ln x = t, d(ln x) = dt, 1x dx = dt. Тогда исходный интеграл примет вид
∫ 
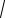 1dt+t2 = ln t +
1dt+t2 = ln t + 
 1+t2 +C = ln ln x +
1+t2 +C = ln ln x + 
 1+ln2 x +C .
1+ln2 x +C .
|
Пример 2.5. Найти неопределенный интеграл ∫ |
|
|
|
x3 |
dx ме- |
||||||||||||||||||||||||||||||||||||||
|
|
(x −1)2 |
||||||||||||||||||||||||||||||||||||||||||
тодом подстановки. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Решение. Пусть x = t +1, |
|
|
dx = d(t +1), dx = dt. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
∫ |
|
|
x3 |
|
|
dx |
= ∫ |
(t +1)3 |
dt |
|
= ∫ |
t3 +3t2 +3t +1 |
dt = |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
(x −1)2 |
|
|
t2 |
|
|
|
|
t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
= ∫ |
t |
dt + ∫ |
3t2t dt + ∫ |
dt =∫ tdt +3∫ 1dt + ∫ 3t dt + ∫ t−2dt = |
|
||||||||||||||||||||||||||||||||||||||
t2 |
t2 |
|
||||||||||||||||||||||||||||||||||||||||||
|
|
t2 |
|
|
|
|
|
|
|
|
|
|
t−1 |
|
|
|
|
|
|
(x −1)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||||||
= |
|
|
|
+3t +3ln |
t |
+ |
|
|
+C = |
|
|
|
|
|
+3(x −1) +3ln |
x −1 |
− |
|
|
|
|
|
|
+C. |
||||||||||||||||||||
2 |
−1 |
|
|
2 |
|
|
|
x |
−1 |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Интегралы, содержащие иррациональные выражения вида |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
a2 − x2 |
, |
|
|
x2 +a2 |
|
или |
|
x2 −a2 |
|
, можно вычислить с пом ощью |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
тригонометрических подстановок. Например, для a2 − x2 |
|
приме- |
||||||||||||||||||||||||||||||||||||||||||
няют |
|
|
|
|
подстановку |
|
|
|
|
x = a sin t , |
|
|
|
dx = a costdt |
|
|
|
|
|
(или |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
x = a cost, |
dx = −a sin tdt) ; |
|
для |
|
|
x2 + a2 |
применяют подстановку |
|||||||||||||||||||||||||||||||||||||
x = a tg t, |
dx = |
|
a |
|
|
dt |
|
|
|
(или |
|
|
x = a ctg t, |
dx = − |
|
|
a |
|
dt); для |
|||||||||||||||||||||||||
cos2 t |
|
|
|
|
|
sin2 t |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
a |
|
|
|
|
a |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
x2 −a2 |
|
применяют подстановку |
|
|
x = |
|
или x = |
|
|
|
. |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
sin t |
|
cost |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
41

Пример 2.6. |
Найти |
∫ |
1− x2 |
|
||||||||
x2 |
|
|
||||||||||
|
|
|
|
|
|
|||||||
Решение. |
|
|
|
|
|
|
|
|||||
|
1− x2 |
|
|
|
|
|
|
|
||||
∫ |
|
|
dx = [x = sin t, |
dx = |
||||||||
x2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
= ∫ |
|
|
1−sin2 t costdt |
= |
|
|||||
|
|
|
|
sin |
2 |
t |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
|
= ∫ |
1 |
dt − ∫ 1dt =−ctgt |
|||||||||
|
sin2 t |
|||||||||||
dx .
costdt, t = arcsin x, −1 ≤ x ≤1 ]=
∫ctg2 tdt = ∫ (sin12 t −1)dt =
−t +C = − 
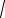 1−x x2 −arcsin x +C.
1−x x2 −arcsin x +C.
2.2.2. Интегрирование некоторых иррациональных функций
Интегралы вида ∫ |
R(x,( ax +b ) |
p |
,...,( ax +b ) |
s |
|
|
|
q |
)dx, где |
R − раци- |
|||||
t |
|||||||
|
cx + d |
cx + d |
|
|
|||
ональная функция, p, q,..., s,t − целые числа, находятся с помощью подстановки t = m cxax++db , где m −наименьшее общее кратное чи-
cxax++db , где m −наименьшее общее кратное чи-
сел q,...,t.
Пример 2.7. Найти ∫ |
x + |
|
|
|
1+ x |
|
dx. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
1+ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Решение. Пусть t = 6 |
|
|
|
|
, тогда |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
1+ x |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
x = t6 −1, dx = 6t5dt, |
|
|
|
|
|
|
|
|
= t5 , |
|
3 |
|
= t2. |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
1+ x |
|
1+ x |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x + |
|
|
|
|
|
|
|
|
t6 |
−1+t3 |
|
|
|
|
|
|
||||||||
Следовательно, |
∫ |
|
1+ x |
|
dx = ∫ |
6t |
5 |
dt = |
||||||||||||||||||||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
t2 |
|
|||||||||||||||||||
|
1+ x |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
7 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|||
= 6∫ (t |
9 |
+t |
6 |
−t |
3 |
)dt = |
t |
|
|
+ |
t |
|
− |
t |
|
|
+C, |
где |
t = |
6 |
1+ x . |
|||||||||||||
|
|
|
6 |
10 |
7 |
4 |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
42
