Задания:

В данных задачах составить экономико-математическую модель.

1. Для производства двух видов изделий А и В предприятие использует три вида сырья. Другие условия задачи приведены в таблице.

Таблица 5

Вид сырья	Общее количество сырья, кг	Нормы расхода сырья на одно изделие, кг
		А	В
S1	300	12	4
S2	120	4	4
S3	252	3	12
Прибыль от реализации изделия, ден. ед.		30	40

Составить такой план выпуска продукции, при котором прибыль предприятия от реализации продукции будет максимальной при условии, что изделий В надо выпускать не менее, чем изделий А.

2. Рацион питания для животных на ферме состоит из двух видов кормов I и II. Один килограмм корма I стоит 80 руб. и содержит: 1 ед. жиров, 3 ед. белков, 1 ед. углеводов и 2 ед. нитратов. Один килограмм корма II стоит 10 руб. и содержит: 3 ед. жиров, 1 ед. белков, 8 ед. углеводов и 4 ед. нитратов.

Составить наиболее дешевый рацион питания, обеспечивающий жиров не менее 6 ед., белков не менее 9 ед., углеводов не менее 8 ед., а нитратов не более 16 ед.

.Общая задача линейного программирования.

Пусть дана система mуравнений и неравенств сnпеременными (неизвестными):

(1)

и линейная функция:

(2)

Найти решение системы X^*(x₁,x₂, …,x_n), где всеx_j0 (для всехjот 0 доn), при котором функцияzпринимает оптимальное значение (максимальное или минимальное).

Такая задача называется задачей линейного программирования (ЗЛП) в общем виде. (1) называется системой ограничений; (2) – целевой функцией (функцией цели).

ЗЛП можно записать в сокращенном виде:

(1^/, 2^/)

Оптимальным решением (планом)ЗЛП называется решение X^*(x₁,x₂,…,x_n) системы ограничений, при котором целевая функция принимает оптимальное значение.

Если система ограничений (1) состоит из одних неравенств (не нарушая общности, будем говорить, что ограничения вида "", так как, если знак неравенства "", то мы можем умножив его на –1 перейти к неравенству вида ""), то такую задачу называют задачей линейного программирования встандартном виде (в стандартной форме).

Если все ограничения системы (1) – уравнения (вида "="), то такую задачу называют задачей линейного программирования в каноническом виде (в канонической форме).

Любая ЗЛП может быть приведена к каноническому виду.

Терема: Любому решению X^*(x₁,x₂,…,x_n) неравенствасоответствует определенное решение X^*(x₁,x₂,…,x_n,x_n+1) уравненияв которомx_n+10.

И обратно.

Приведем ограничение (1) к каноническом виду:

Геометрический смысл решений неравенств и их систем.

Рассмотрим линейные неравенства с двумя переменными.

Теорема: Множеством решений линейного неравенства с двумя переменнымиявляется одна из двух полуплоскостей, на которые вся плоскость делиться граничной прямой, включая и эту прямую. А другая полуплоскость с этой же прямой будет являться решением неравенства.

Если полуплоскость является решением линейного неравенства, то все точки данной полуплоскости удовлетворяют неравенству, то есть превращают его в истинное утверждение при подстановке в неравенство координат точки. Если полуплоскость не является решением неравенства, то ни одна его точка не удовлетворяет неравенству, то есть, при подстановки ее координат в неравенство превращает его в ложное утверждение. Следовательно, чтобы выбрать полуплоскость, являющуюся решением неравенства, достаточно проверить истинность или ложность неравенства в любой точке любой полуплоскости. Обычно, если прямая не проходит через начало координат, принято проверять истинность неравенства в точке (0;0).

Теорема: Множеством решений совместной системыmлинейных неравенств с двумя переменными:

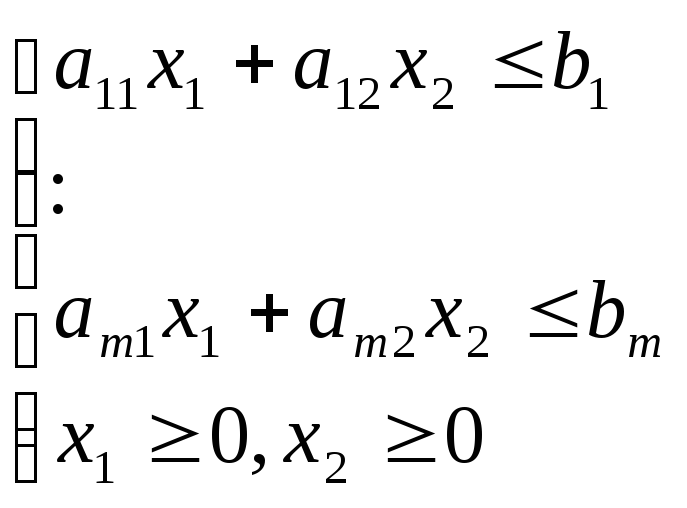является выпуклым многоугольным множеством, которое является пересечением полуплоскостей, которые являются решениями каждого неравенства системы.

Таким образом, чтобы решить систему линейных неравенств графически, необходимо на одном графике решить все неравенства, а затем выбрать их общую часть.

Пример. Решить систему неравенств:

Построим граничную прямую для первого неравенства: (I). Она проходит через точки:

х1	0	-4
х2	5	0

Построим граничную прямую для второго неравенства: (II). Она проходит через точки:

х1	0	12
х2	8	0

Построим граничную прямую для третьего неравенства: (III). Она проходит через точки:

х1	0	-4
х2	5	0

Граничной прямой четвертого неравенства будет ось Ох₂.

Граничными прямыми пятого и шестого неравенств будут соответственно ось Ох₁и прямая х₂=6.

Найдем полуплоскости, которые будут являться решениями данных неравенств, подставляя в каждое координаты точки (0;0).

Получим общую область OABCDE(см. рисунок )

Рисунок 1

При решении системы неравенств не всегда получается замкнутая многоугольная область. Может получиться бесконечна область, одна точка. Если система неравенств несовместна, то все полуплоскости не пересекаются. Возможные варианты показаны на рисунке.

Рисунок 2