Задания:

Найти смешанные стратегии игроков и цену игры:

1.

-2	2
1	-1

2.

2	3
1	2

3.

4	-2
1	3

Нелинейное программирование. Классическое определение экстремума.

Во многих экономических моделях исследования операций зависимость между постоянными и переменными функции можно считать линейной лишь в первом приближении. Более детальное рассмотрение обнаруживает их нелинейность. Как правило, прибыль, себестоимость, капитальные затраты на производстве в действительности зависят от ресурсов, объема производства и т.д. нелинейно.

В общем виде задача нелинейного программирования имеет вид:

,

где к целевой функции и ограничениям переменных нет требования линейности.

Можно выделить класс нелинейных задач, которые относятся к классическим методам оптимизации. Для них выполнены условия:

• среди ограничений нет неравенств;

• необязательны условия неотрицательности переменных;

• нет дискретных переменных;

• m<n(число ограничений меньше числа неизвестных);

• непрерывны и имеет частные производныеIIпорядка.

Задача нелинейного или математического программирования ставится следующим образом: найти переменные , удовлетворяющие условиями обращающим в максимум (минимум) функцию.

Пример 19:

Фирма для производства продукции расходует два средства (например труд и капитал). х₁и х₂- затраты факторов производства. Факторы производства будем считать взаимозаменяемыми, т.е. можно применять такие методы производства, при которых величина затрат капитала в соответствии с величиной затрат труда оказывается больше или меньше (трудоемкость производства). Объем производства является функцией затрат производства(производственная функция) Издержки зависят от расходов обоих факторови от цен этих факторов. Совокупные издержки:. Требуется при данных совокупных издержках определить такое количество факторов производства, которое максимизирует объем продукцииz.

Математическая модель:

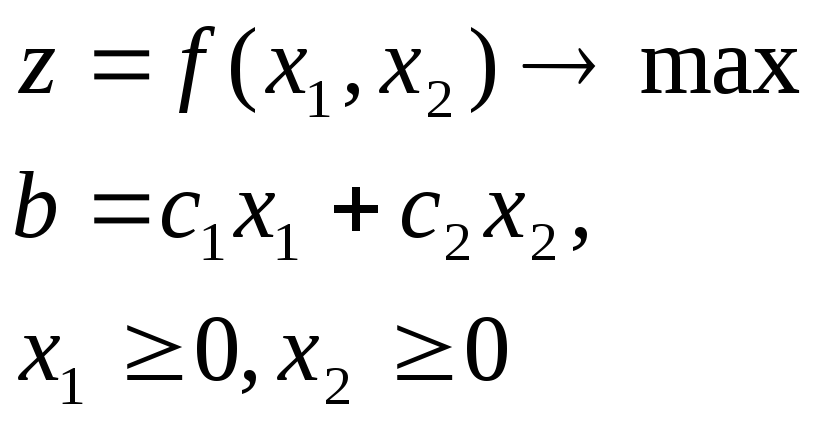
Для решения данного класса задач применяются методы классической оптимизации.

Введем понятие экстремума.

Пусть функция дважды дифференцируема в точкеи в некоторой ее окрестности. Если для всех точек Х из этой окрестности выполнено:илитоимеетлокальный экстремумв точке(максимум или минимум соответственно).

Точка , в которой все частные производные равны 0, называетсястационарной точкой.

Необходимое условие существования экстремума.

Если в точке функцияимеет экстремум, то первые производные в этой точке равны 0:

, то есть все точки экстремума удовлетворяют системе уравнений:

.

Однако необходимое условие не является достаточным. Для получения достаточного условия необходимо определить знак дифференциала второго порядка .

Достаточное условие существования экстремума:

1. в точке функцияимеет максимум, еслии минимум, если, для всех, не обращающихся в ноль одновременно ();

2. если может принимать, в зависимости отто положительные, то отрицательные значения, то в точке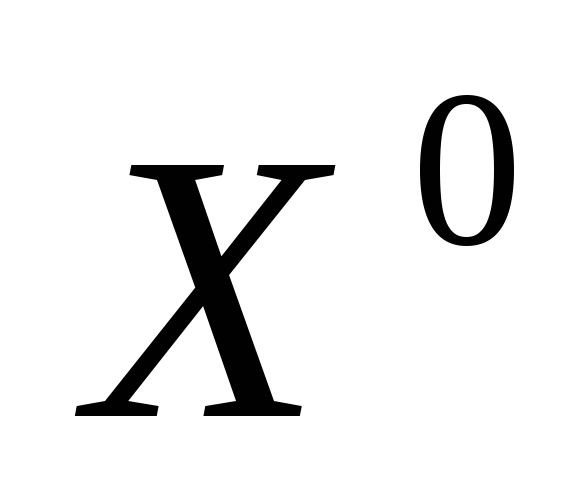экстремума нет;

3. если может обращаться в ноль, не только при нулевых приращениях, то вопрос о существовании экстремума в точкеостается открытым.

Для функции двух переменных достаточное условие существования экстремума еще не очень сложны. Существует четыре частных производных второго порядка:, причем смешанные производные, если непрерывны, то равны.

Найдем значение частных производных второго порядка в стационарной тоске :

.

Обозначим через определитель, составленный из:

.

Тогда достаточное условие функции двух переменных имеет вид:

1. если , то в точкемаксимум; если, то в точкефункция достигает минимума ();

2. если , то экстремума нет;

3. если , то вопрос об экстремуме остается открытым.

Пример 20.

Исследовать на экстремум функцию .

Решение.

Найдем частные производные:

.

Приравниваем их нулю:

Решая полученную систему, находим три стационарные точки .

Найдем вторые частные производные:

Вычислим значения вторых частных производных в каждой стационарной точке, составим определитель и применим достаточные условия.

В точке

.

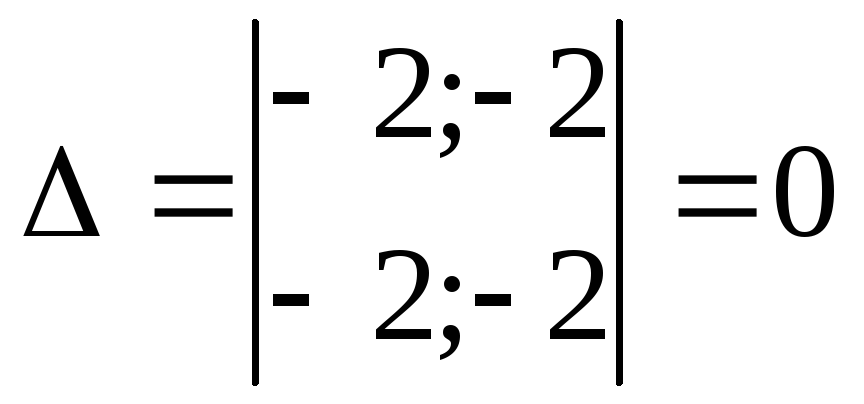Вопрос об экстремуме остается открытым (такая точка называется седловой).

В точке , а также в точке

.

Функция в этих точках имеет минимум, так как .