Задания:

Решить задачи графическим методом:

Задача № 1

Задача № 2

Задача № 3

Задача № 4

Задача № 5

Задача № 6

Особые случаи задач линейного программирования. (графический метод) Неограниченность области допустимых решений.

Решим геометрически следующую задачу:

Из рисунка 2 видно, что область допустимых значений неограниченна. Перемещая линию уровня функции zв направлении убывания целевой функции (т.е. в направлении, противоположном вектору_z), убедимся, что она всегда будет пересекать область допустимых значений, следовательно, целевая функция неограниченно убывает.

Ответ будет звучать следующим образом: минимум функции не ограничен, z_min=-.

Внимание!В некоторых случаях неограниченности области допустимых решений целевая функция может достигать своего оптимума.

Рисунок 4

Не единственность оптимального решения.

Рассмотрим задачу:

Геометрическое решение задачи показано на рисунке 3. Из него следует, что линия уровня с максимальным уровнем совпадает с граничной линией АВ области допустимых решений ABCD, т.е. с линией х₁+х₂=8 (Внимание!Данная ситуация возможна только в том случае, если коэффициенты целевой функции пропорциональны коэффициентам какой-либо прямой ограничений. Это условие необходимое, но не достаточное.). Следовательно, на всем отрезке АВ целевая функцияzпринимает одно и то же оптимальное значение. Это означает, что задача имеет бесконечное множество оптимальных решений (их задают координаты отрезка АВ), среди которых базисных оптимальных решений два -–соответственно в угловых точках А(3,5) и В(6,2) (точки находим решая соответствующие уравнения). Точки отрезка АВ задаются как линейная комбинация точек А и В:

Максимальное значение целевой функции можно найти, подставив координаты любой точки отрезка АВ в уравнение целевой функции.

В нашем случае z=24.

Рисунок 5

Задания:

Решить задачи геометрически:

1.

2.

3.

4.

5.

6.

7.

Системыmлинейных уравнений сnнеизвестными.

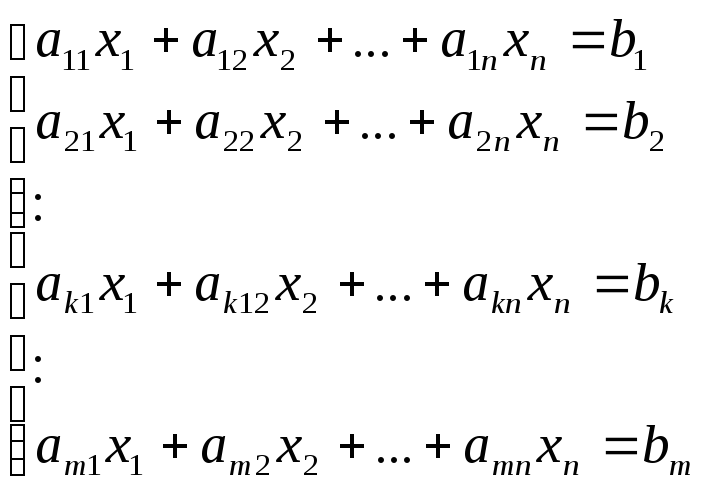
В задачах ЛП представляют интерес системы линейных уравнений в которых ранг (r) матрицы системы (A) меньше чем число переменныхn.

Рассмотрим системы в которых mуравнений независимы, то есть, (m<n).

Любые переменных системы уравнений с nпеременными (m<n) называютсяосновнымиилибазисными, если определитель матрицы коэффициентов при них отличен от нуля.

Остальные n-mпеременных называютсянеосновнымиилисвободными.

Максимально возможное число наборов базисных переменных .

Пример.

Число возможных наборов базисных переменных равно:

Возможные наборы базисных переменных: х₁х₂; х₁х₃; х₁х₄; х₂х₃; х₂х₄; х₃х₄.

Проверим, действительно ли все эти наборы переменных могут быть базисными.

Посчитаем определитель для набора х₁х_{2: .}Следовательно, переменные х₁х₂можно выбрать базисными.

Посчитаем определитель для набора х₄х_{3: .}Следовательно, переменные х₂х₃ нельзя выбрать базисными.

Остальные наборы переменных проверить самостоятельно.

Решение системы линейных уравнений X(x₁,x₂,…,x_n) называетсядопустимым, если все компоненты решения неотрицательны (). Если это не так, то решение системы называетсянедопустимым.

Базисным решениемсистемыmлинейных уравнений сnпеременными называется такое решение, в котором неосновные переменные равны нулю.

Пример.

Рассмотрим условие предыдущего примера. Возьмем за базис переменные х₁х_2. Следовательно, в базисном решении переменные х₃х₄будут равны 0. Получим:

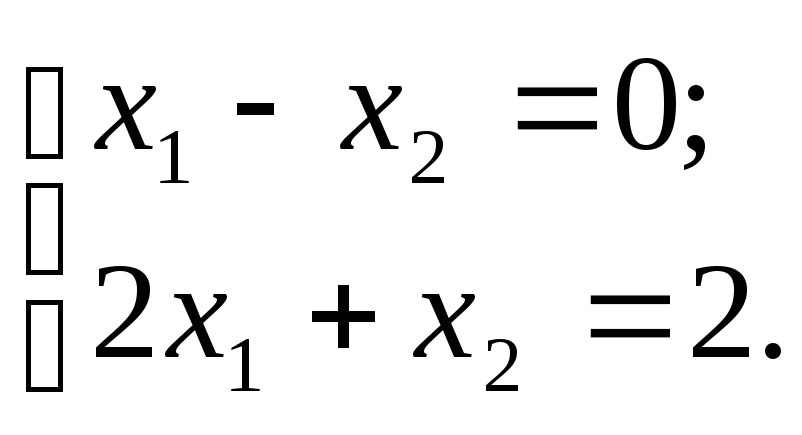
Решив систему уравнений получим х₁=2/3, х₂=2/3.

А все базисное решение будет иметь вид: (2/3; 2/3; 0; 0).