
Лосев-КлячинМиклюков МА в КИ
.pdf
§10. Биномиальные дифференциалы. Теорема Чебышева |
171 |
Доказательство. Мы докажем лишь часть теоремы, показав, что в случае, когда одно из чисел p, q или p + q — целое, интеграл (2) сводится к интегралу от рациональной функции. Оставшаяся часть теоремы очень сложна и требует привлечения методов алгебры, которые нам пока недоступны.
Итак, пусть p — целое. Поскольку q — рационально, то оно представимо в виде несократимой дроби α/β, где α и β — целые. Сделаем подстановку
|
t = uβ, dt = βuβ−1 du . |
Тогда |
|
|
J= β uα (a + buβ)p uβ−1 du,
имы получили интеграл от рациональной функции.
Пусть q – целое. Здесь имеем p = α/β, где α и β – целые. Возможна подстановка
t |
|
1 |
( |
uβ |
− |
a , dt |
= |
β |
uβ−1 du , |
= b |
|
||||||||
|
|
) |
b |
||||||
и мы приходим к интегралу от рациональной функции
|
|
β |
|
1 |
|
|
|
|
|
|
|
|
||||
J = |
|
|
|
(uβ − a)q uα uβ−1 du . |
||||||||||||
b |
bq |
|||||||||||||||
Пусть (p + q) — целое. В этом случае |
||||||||||||||||
J = |
|
|
|
a |
p |
|||||||||||
tp+q |
|
|
+ b |
dt , |
||||||||||||
t |
||||||||||||||||
где |
|
|
|
|
a |
|
|
|
1/β |
|
|
|||||
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
|||
p = |
|
, |
|
|
|
+ b |
= u . |
|||||||||
β |
|
t |
||||||||||||||
После подстановки |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
a |
|
|
|
, dt = − |
β a uβ−1 |
||||||||
t = |
|
|
|
du |
||||||||||||
uβ − b |
(uβ − b)2 |
|||||||||||||||
также приходим к интегралу от рациональной функции
J = −β a |
ap+q |
|
uβ−1 |
|||||||
|
|
|
|
uα |
|
|
du . |
|||
(uβ − b)p+q |
(uβ − b)2 |
|||||||||
ПРИМЕР 1. Вычислим интеграл |
|
|
|
|||||||
3 |
1 + √4 |
|
|
|
|
|||||
x |
|
|
|
|||||||
I = |
|
√ |
|
|
dx. |
|||||
x |
||||||||||

172 Глава 8. Неопределенный интеграл
Мы имеем
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
= t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
x4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
I = x−2 |
1 + x4 3 dx = |
|
|
x = t4 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
= |
|
1 |
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx = 4t3 dt |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
u = (1 |
+ t)3 |
|
|
|||||||||||||||||||
= t−2(1 + t)3 4t3dt = 4 t(1 + t)3 dt = |
|
|
|
t = u3 |
|
|
1 |
|
|
= |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 3u2−du |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
= 12 (u3 − 1) u3 du = |
|
|
|
u7 − 3u4 + C = |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
7 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
12 |
|
|
|
7 |
|
|
|
|
|
4 |
|
|
|
|
|
|
12 |
|
|
|
|
|
|
1 |
|
7 |
|
|
|
|
|
|
|
|
|
|
1 |
4 |
|
|
|
|
|||||||||||||
= |
|
(1 + t)3 |
− 3(1 + t)3 |
+ C = |
|
|
|
|
(1 + x4 )3 |
− 3(1 + x4 )3 |
+ C. |
||||||||||||||||||||||||||||||||||||||||||||
7 |
7 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
ПРИМЕР 2. (1986) Вычислим интеграл |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
I = |
|
|
|
√4 |
|
|
|
dx |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + x4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Выполнив подстановку |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
x4 = t, |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
x = t |
4 , |
|
|
|
|
|
dx = |
|
|
t−4 |
|
dt, |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
I = (1 + x4)−4 dx = |
|
|
t− |
4 |
(1 + t)−4 |
dt = |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
4 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−41 |
|
|
|
|
|
|
|||
|
|
|
4 |
|
|
t |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
u |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−4u |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
= 1 |
|
|
t−1 1 |
|
|
|
−4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
4 |
|
|
|
|
|
|
|
|
= |
|
|
|
|
|||||||||
|
|
|
|
|
+ 1 dt = |
|
|
|
t = |
|
1 uu4 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
4 |
2 du |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
(1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u ) |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
= |
|
|
(1 |
− |
u )u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
du |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
u4 (1 − u4)2 |
du = |
1 |
− u4 |
. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Раскладываем на сумму простых дробей. Имеем |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
1 |
|
= |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
A |
+ |
|
|
|
|
B |
|
|
+ |
|
Cu + D |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
1 − u4 |
(1 − u)(1 + u)(1 + u2) |
|
1 − u |
1 + u |
1 + u2 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
и, далее,
1 = u3(A−B −C)+u2(A+B −D)+u(A−B +C)+A+B +D.

§11. Метод Остроградского |
173 |
Решая систему
A − B − C = 0 A + B − D = 0
A − B + C = 0 A + B + D = 1,
находим A = B = 1/4, C = 0 и D = 1/2. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
Таким образом, получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||
|
|
|
I = |
|
1 |
|
+ |
|
|
|
|
+ |
|
|
|
|
dx = |
|
|
|
|||||||||||||
4(1 |
|
u) |
4(1 + u) |
2(1 + u2) |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
= |
|
|
− ln |1 − u| + ln |1 + u| + |
|
arctg u |
+ C1 = |
|
|
|
||||||||||||||||||||||||
4 |
2 |
|
|
|
|||||||||||||||||||||||||||||
1 |
|
− ln 1 − (1/t + 1)−1/4 + ln 1 + (1/t + 1)−1/4 + |
|
|
|||||||||||||||||||||||||||||
= |
|
|
|
|
|||||||||||||||||||||||||||||
4 |
|
|
|
||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
1/4 |
|
|
|
|
|
4 |
− |
|
|
− |
|
4 |
|
|
|
1/4 |
|
||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
+ |
|
arctg (1/t + |
1)− |
|
|
|
+ C1 = |
|
|
ln |
1 |
|
1/x |
+ 1 |
− |
|
|
+ |
|||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
4 |
|
|
−1/4 |
1 |
|
|
|
|
4 |
|
−1/4 |
|
|
|
|
|
|||||||||||||
|
|
|
|
1/x + 1 |
|
|
|
|
|
|
|
|
|
1/x |
+ 1 |
|
|
+ C1. |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
+ ln 1 + |
|
|
|
+ 2arctg |
|
|
|
|
||||||||||||||||||||||||
§11. Метод Остроградского выделения рациональной части интеграла
Пусть P (x)/Q(x) – правильная несократимая дробь и пусть ее знаменатель Q(x) разложен на простые сомножители, т.е.
Q(x) = (x − a)k . . . (x2 + px + q)m . . . . |
(1) |
Тогда интеграл от этой дроби представим в виде суммы интегралов от простых дробей. Именно,
|
|
P (x) |
|
|
|
A |
· · ·+ |
M x + N |
|
||||||||||||
|
|
dx = |
|
|
dx + |
|
|
|
dx + . . . . |
||||||||||||
Q(x) |
(x − a)k |
(x2 + p x + q)m |
|||||||||||||||||||
Если k > 1, то |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
A |
|
A |
|
||||||||||
|
|
|
|
|
|
|
dx = − |
|
|
|
1 |
+ C. |
(2) |
||||||||
|
|
|
|
(x − a)k |
k − 1 |
(x − a)k−1 |
|||||||||||||||
Если m > 1, то на основании рекуррентной формулы |
|
||||||||||||||||||||
|
|
|
|
|
M x + N |
|
|
|
|
M x + N |
|
||||||||||
|
|
|
dx = |
|
+ |
|
|||||||||||||||
|
|
(x2 + p x + q)m |
(x2 + p x + q)m−1 |
|
|||||||||||||||||

174 |
|
|
|
|
|
|
|
|
|
|
Глава 8. Неопределенный интеграл |
|||||||||||
+α |
|
|
|
|
dx |
|
|
M x + N |
|
|
M x + N |
|||||||||||
|
|
|
|
= |
|
|
+ |
|
|
|
+ |
|||||||||||
|
(x2 + p x + q)m−1 |
(x2 + p x + q)m−1 |
(x2 + p x + q)m−2 |
|||||||||||||||||||
|
+β |
|
(x2 + p x + q)m−2 = · · · = |
(x2 + p x + q)m−1 + |
||||||||||||||||||
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
M x + N |
|
|
|
|||||
|
+ |
|
|
M x + N |
|
+ · · · + λ |
|
|
dx |
, |
|
|
||||||||||
|
(x2 + p x + q)m−2 |
x2 + p x + q |
|
|
||||||||||||||||||
имеем |
|
|
|
|
M x + N |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
dx = |
|
|
|
||||||||||||
|
|
|
|
|
(x2 + p x + q)m |
|
|
|
||||||||||||||
|
|
|
= |
R(x) |
|
|
|
+ λ |
|
|
|
dx |
(3) |
|
||||||||
|
|
|
|
|
|
|
. |
|
||||||||||||||
|
|
|
(x2 + p x + q)m−1 |
|
x2 + p x + q |
|
||||||||||||||||
Здесь R(x) – многочлен степени более низкой, чем знаменатель, и λ – постоянная. Таким образом, на основании (2) и
(3) мы можем записать
|
|
P (x) |
|
|
|
A |
|
||||
|
|
|
dx = слагаемые вида |
|
|
|
|
+ |
|||
|
Q(x) |
(x − a)k−1 |
|||||||||
|
|
|
|
|
R(x) |
|
|||||
|
+ слагаемые вида |
|
|
|
|
+ |
|||||
|
(x2 + px + q)m−1 |
||||||||||
|
|
+ интегралы вида |
|
A |
dx + |
|
|||||
|
|
x a |
|
||||||||
|
|
|
− |
|
|||||||
|
|
|
|
|
|
γdx |
|
||||
|
|
+ интегралы вида |
|
. |
|
||||||
|
|
x2 + px + q |
|
||||||||
Объединяя теперь однотипные слагаемые, выводим следу-
ющую формулу, впервые найденную Остроградским5 |
|
||||||||
|
P (x) |
P1(x) |
+ |
|
P2(x) |
(4) |
|||
|
dx = |
|
|
|
|
dx. |
|||
Q(x) |
Q1(x) |
Q2(x) |
|||||||
Так как рациональная часть интеграла P1(x)/Q1(x) получена от сложения выделенных рациональных частей, то она является правильной дробью со знаменателем
Q1(x) = (x − a)k−1 . . . (x2 + px + q)m−1 . . . .
5Остроградский Михаил Васильевич (24.9.1801-1.1.1862). Род. в с. Пашенная (ныне Полтавская обл., Украина). Один из основателей петербургской математической школы. Член Петербургской АН (1830), Парижской АН (1856) и др. Автор ряда исследований в области математики и механики, дифференциального и интегрального исчисления, высшей алгебры, геометрии, теории чисел, математической физики и др.

§11. Метод Остроградского |
175 |
Дробь P2(x)/Q2(x), стоящая под знаком интеграла, получена от сложения дробей вида 1/(x − a)... и 1/(x2 + px + q)..., а потому
Q2(x) = (x − a) . . . (x2 + px + q) . . . .
В силу разложения (1), имеем |
|
Q(x) = Q1(x) Q2(x). |
(5) |
С другой стороны, дифференцируя равенство (4), можно записать
P (x) |
|
P1(x) |
|
|
P2(x) |
|
|
|
= |
|
|
+ |
|
. |
(6) |
Q(x) |
Q1(x) |
Q2(x) |
|||||
Мы видим, что многочлены Q1(x) и Q2(x) легко вычисляются, если известно разложение (1) многочлена Q(x).
Перейдем к методу нахождения числителя в формуле (6). Пусть n, n1, n2 — степени многочленов Q, Q1, Q2 соответственно. Ясно, что n = n1 + n2. Степени многочленов
P , P1, P2 не будут превышать n − 1, n1 − 1, n2 − 1. Подставим в качестве P1 и P2 многочлены степени n1 −1 и n2 −1
с буквенными коэффициентами. Имеем
P1 = a1xn1−1 + a2xn1−2 + · · · + an1−1x + an1 ,
P2 = b1xn2−1 + b2xn2−2 + · · · + bn2−1x + bn2 .
Всего неизвестных ak и bk ровно n1 + n2 = n. Выполним в
(6) дифференцирование
|
|
|
|
|
P |
|
|
P Q |
1 |
− |
P Q |
P |
2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
= |
1 |
|
1 |
1 |
+ |
|
. |
|
|
|
(7) |
||||||
|
|
|
|
Q |
|
|
|
Q2 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
Заметим, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
P Q |
1 |
|
P Q |
|
P Q |
|
P |
H |
|
|
|
Q |
Q |
|
||||||||||
|
1 |
− |
1 |
|
1 |
= |
1 |
|
2 − |
1 |
|
, |
H = |
1 |
2 |
. |
(8) |
|||||||
|
|
|
Q2 |
|
|
|
|
|
|
Q Q |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q |
|
||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
1 |
|
|
Далее заметим, что H является целым многочленом. Дей-
ствительно, если выражение (x − a)k, k ≥ 1, входит множителем в Q1, то (x − a)k−1 входит в Q1, а (x − a) — в Q2. Аналогично с множителем (x2 + px + q)m при m ≥ 1.
Таким образом, можно считать, что H — целый многочлен степени n2 −1. Подставляя (8) в (7), приходим к соотношению
P |
|
= |
P1Q2 − P1H |
+ |
P2Q1 |
|
Q |
Q |
Q1Q2 |
||||
|
|
|||||
или, отбрасывая знаменатель,
P |
= |
P |
Q |
2 − |
P |
H |
+ |
P Q . |
(9) |
|
1 |
|
1 |
|
2 1 |

176 |
Глава 8. Неопределенный интеграл |
Приравнивая коэффициенты этих многочленов, получим n линейных уравнений для определения ak и bk. Так как существование соотношения (6) доказано, то система (9) должна быть разрешимой.
ПРИМЕР 1. Выделить рациональную часть интеграла
4x4 + 4x3 + 16x2 + 12x + 8 dx. (x + 1)2(x2 + 1)2
Мы имеем
Q2 = (x + 1)(x2 + 1) = Q1 = x3 + x2 + x + 1.
Значит, в силу (6), |
|
|
|
|
|||
4x4 |
4x3 + 16x2 + 12x + 8 |
= |
ax2 + bx + c |
|
|
||
|
|
+ |
|
|
+ |
||
|
|
(x + 1)2(x2 + 1)2 |
x3 + x2 + x + 1 |
||||
dx2 + ex + f
+x3 + x2 + x + 1
и, далее,
4x4 + 4x3 + 16x2 + 12x + 8 = (2ax + b)(x3 + x2 + x + 1)−
−(ax2 + bx + c)(3x2 + 2x + 1) + (dx2 + ex + f)(x3 + x2 + x + 1).
Приравняем коэффициенты при одинаковых степенях. Находим
|
|
d = 0 |
d = 0 |
|
|
|
|
−a + d + e = 4 |
c = −4 |
|
|
|
|
−2b + d + e + f = 4 |
b = 1 |
|
|
|
|
a − b − 3c + d + e + f = 16 |
a = −1 |
|
|
|
|
2a − 2c + e + f = 12 |
e = 3 |
|
|
|
|
b − c + f = 8 |
f = 3. |
|
|
Таким образом, окончательно получаем |
|
|
|||
|
4 x4 |
+ 4 x3 + 16 x2 + 12 x + 8 |
dx = |
−x2 + x − 4 |
+ |
|
|
(x + 1) (x2 + 1) |
|||
|
(x + 1)2 (x2 + 1)2 |
|
|||
+3 arctg x + C.

Глава 9
Определенный интеграл
§1. Понятие определенного интеграла
Пусть f – функция, определенная на [a, b]. Произвольный упорядоченный набор точек
a = x0 ≤ x1 ≤ · · · ≤ xn = b
назовем разбиением Tn отрезка [a, b] на отрезки [x0, x1],
[x1, x2], . . . , [xn−1, xn]1 или просто разбиением Tn. Наибольшую из длин ∆xi = xi+1 − xi отрезков [xi, xi+1] назовем мелкостью разбиения Tn и обозначим через µ(Tn). Другими словами,
µ(Tn) = max ∆xi.
0≤i≤n−1
Если на каждом из отрезков [xi, xi+1] разбиения Tn выбрано по точке xi ≤ ξi ≤ xi+1, то полученный объект будем называть разбиением с отмеченными точками отрезка [a, b] и
обозначать T˙n. Величина
n−1
S(T˙n) = f(ξk)∆xk
k=0
называется интегральной суммой Римана2, соответствующей разбиению с отмеченными точками T˙n.
ОПРЕДЕЛЕНИЕ 1.1. Если существует конечный предел
lim S(T˙n), |
(1) |
µ(Tn)→0 |
|
не зависящий от выбора последовательности разбиений {T˙n} с мелкостью µ(Tn) → 0, то этот предел называется опреде-
1всего n отрезков
2Риман Георг Фридрих Бернхард (17.9.1826-30.7.1866). Род. в Нижней Саксонии (Германия). Автор ряда значительных исследований в области теории функций комплексного переменного, математической физике, топологии, геометрии и др.
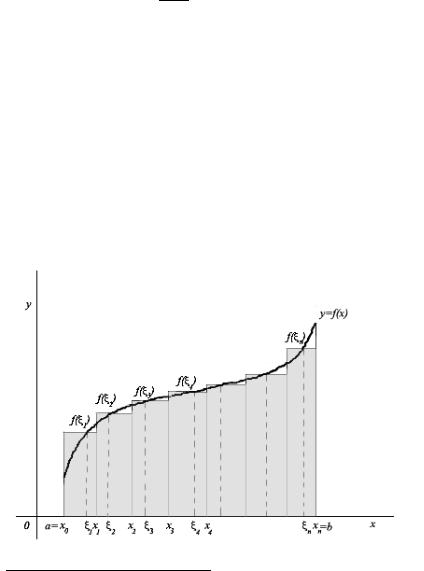

§3. Физический смысл определенного интеграла |
179 |
Пусть задана непрерывная и неотрицательная функция f(x).
Тогда
n
S(T˙n) = f(ξi)∆xi =
i=1
=f(ξ1)(x1 − x0) + f(ξ2)(x2 − x1) + · · · + f(ξn)(xn − xn−1)
–площадь ступенчатой фигуры. При измельчении разбиения ступенчатая фигура все лучше и лучше аппроксимирует кри-
волинейную трапецию так, что lim S(T˙n) — площадь кри-
µ(Tn)→0
волинейной трапеции4.
Если f отрицательна, то величина интеграла
b
f(x) dx
a
совпадает с площадью криволинейной трапеции, взятой со знаком минус. В общем случае, если f меняет знак, то этот интеграл равен сумме взятых с соответствующими знаками площадей криволинейных трапеций.
§3. Физический смысл определенного интеграла
Предположим, что тело движется прямолинейно и его ускорение, как функция времени t, подсчитывается по формуле a = a(t). Определим скорость тела v = v(t) в момент времени t > 0, зная, что v(0) = v0. Устроим разбиение Tn отрезка [0, t]. На каждом из отрезков [ti, ti+1] можно приближенно принять ускорение постоянным и равным a(ξi). Тогда за промежуток времени от t = ti до t = ti+1 скорость v получит приращение, приближенно равное
a(ξi)(ti+1 − ti) = a(ξi)∆ti,
а за все время от 0 до t имеем
n−1
v(t) − v(0) ≈ a(ξi) ∆ti,
i=0
т.е. v(t) − v(0) ≈ S(T˙n). Переходя к пределу, находим
|
|
|
|
|
|
|
t |
v t |
v |
|
lim |
S(T˙ |
|
) = |
a(τ) dτ, |
( ) − |
|
(0) = |
µ(Tn)→0 |
|
n |
|
0 |
4Точное определение понятия площади фигуры будет приведено ниже (Глава 11. Приложения определенного интеграла).

180 |
Глава 9. Определенный интеграл |
|
т.е. |
|
|
v(t) = t |
a(τ) dτ + v(0). |
(1) |
0
Здесь τ – ”немая” переменная, т.е. переменная, которую можно записать любым другим символом или буквой за исключением v, a, t – уже используемых.
Аналогично, по известной мгновенной скорости v(t) мы всегда можем определить путь, пройденный телом за промежуток времени [0, t], по формуле
t |
(2) |
S(t) = v(x) dx. |
0
Формулы (1) и (2) имеют важные применения в технических конструкциях. Рассмотрим следующий известный пример.
ПРИМЕР 1. Представим себе полностью закрытый, без окон, объект, движущийся по прямой. Находящийся внутри объекта наблюдатель должен определить пройденное расстояние с помощью измерений и вычислений, выполненных внутри объекта без каких-либо контактов с внешним миром.
Если объект движется с постоянной скоростью, то наблюдатель не замечает движения и не имеет возможности обнаружить движение никакими механическими опытами. Это есть классический принцип относительности Галилея.5
В то же время каждый из нас, хотя бы раз ездивший в трамвае, знает, что уcкорение можно определять, не глядя в окно. К примеру, пружина с жестко закрепленным одним из концов, расположенная внутри объекта по ходу направления движения, при ускорениях сжимается либо растягивается. Таким образом, наблюдатель, находящийся внутри объекта, может определять ускорение a(t) в момент времени t посредством измерений длины пружины.
Допустим, что в начальный момент времени объект находился в состоянии покоя, т.е. v(0) = 0. Зная ускорение a(t), по формулам (1), (2) можно вычислять скорость v(t) и путь S(t), пройденный за время t, т.е. наблюдатель может определять свое положение в любой момент времени.
5Равномерное движение не может быть обнаружено никакими опытами внутри
объекта, связанными с электромагнитными явлениями, например, распространением света. Это — принцип относительности Эйнштейна.
Галилей Галилео (15.2.1564–8.1.1642) – физик, механик, астроном и математик. Род. в Пизе (Италия). Один из основателей точного естествознания.
Эйнштейн Альберт (14.3.1879–18.4.1955) – физик и математик. Род. в Ульме (Германия). Создатель спец. теории относительности, общей теории относительности, квантовой концепции света, автор работ по теории броуновского движения и др.
