Лосев-КлячинМиклюков МА в КИ

этой целью воспользуемся выражением для остаточного члена в форме Лагранжа. Имеем при x = 1

Таким образом, чтобы вычислить, например, число e с точностью до 10−37, достаточно выбрать n столь большим, чтобы было

§5. Приложения формулы Тейлора к исследованию графиков функций

Мы знаем, что если f (x0) = 0 и f (x0) > 0, то f имеет в точке x0 локальный минимум; если же f (x0) = 0 и

f (x0) < 0, то – локальный максимум. Случай f (x0) = f (x0) = 0 остался неисследованным.

Рассмотрим общую ситуацию. Предположим, что в окрестности точки x = x0 функция имеет n производных и n-я производная в точке x0 не обращается в нуль, а

f (x0) = ... = f(n−1)(x0) = 0. Воспользуемся формулой Тейлора с остаточным членом в форме Пеано. Имеем

При x, близких к x0, знак f(n)(x0) + ε(x) совпадает со знаком

n!

f(n)(x0). Рассмотрим два случая

а) n – четное. Тогда (x − x0)n > 0 и знак приращения f(x)−f(x0) совпадает со знаком f(n)(x0). Следовательно, при f(n)(x0) > 0 точка x0 есть точка локального минимума, а при f(n)(x0) < 0 – точка локального максимума.

б) n – нечетное. Пусть f(n)(x0) > 0. Тогда при x < x0

множитель (x − x0)n в (1) меньше нуля и f(x) − f(x0) < 0, при x, близких к x0, а при x > x0 множитель (x − x0)n в

(1) больше нуля и f(x) − f(x0) > 0, при x, близких к x0. Следовательно, x0 – точка перегиба.

Аналогично и в случае, когда f(n)(x0) < 0.

ТЕОРЕМА 5.1. Если из производных, отличных от нуля, первой оказывается производная нечетного порядка (больше 1), то точка x0 – точка перегиба. Если таковой является производная четного порядка, то x0 – точка локального максимума либо локального минимума в зависимости от того, будет ли ее знак отрицательный либо положительный.

Удобное правило для запоминания. Если

f (x0) = ... = f(n−1)(x0) = 0 и f(n)(x0) = 0, то f(x) ведет себя в окрестности x0 как функция k(x − x0)n, где k = f(n)(x0).

Следовательно, точка x = 0 – точка перегиба.

Глава 7

Выпуклые функции

§1. Понятие выпуклой функции

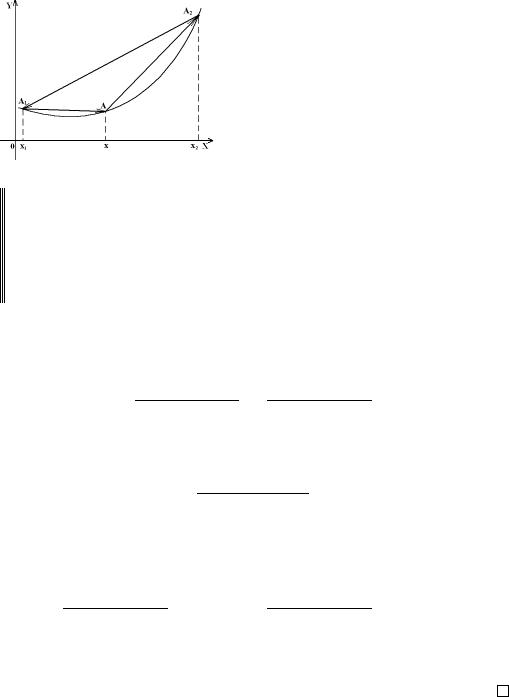
ОПРЕДЕЛЕНИЕ 1.1. Функция f, определенная и непрерывная в промежутке a, b , называется выпуклой вниз, если для произвольных значений x1, x2 из промежутка a, b и любого q (0, 1) выполняется неравенство

Очевидно, что если f – выпукла вниз, то (−f) – выпукла вверх и обратно.

Геометрический смысл.

Пусть x = qx1 + (1 − q)x2, где x1 < x2. Тогда, очевид-

но, x1 < x < x2.

Обратно, всякое число x такое, что x1 < x < x2, представимо в виде

x = qx1 + (1 − q)x2 при

В левой части соотношения (1) записана ордината точки A, в правой части (1) – ордината точки B. Таким образом, выпуклая вниз функция характеризуется тем, что для произвольной поддуги ее графика все точки этой поддуги лежат не выше стягивающей поддугу хорды. (В случае выпуклой вверх функции – не ниже.)

УПРАЖНЕНИЕ 1. Попробуйте дать свое определение вогнутой и выпуклой функции. Заметим, что у различных авторов определения – диаметрально противоположные (см., например, Г.М. Фихтенгольц "Курс дифференциального и интегрального исчисления"и "Математический энциклопедический словарь" под ред. Ю.В. Прохорова). В связи с этим, предлагаем учесть нюансы русского языка.

§2. Простейшие свойства выпуклых функций

ТЕОРЕМА 2.1. Произведение выпуклой вниз функции на положительную постоянную – выпуклая вниз функция. Произведение выпуклой вниз функции на отрицательную постоянную – выпуклая вверх функция.

Доказать самостоятельно.

ТЕОРЕМА 2.2. Сумма двух выпуклых вниз функций – также выпуклая вниз функция.

Доказать самостоятельно.

1

ПРИМЕР 1. Функция y = −x3 , заданная на множестве x > 0, является выпуклой вниз, однако функция

изведение 2-х выпуклых вниз функций может не являться выпуклой вниз функцией.

ТЕОРЕМА 2.3. Если ϕ(u) – возрастающая, выпуклая вниз функция, а u = f(x) также выпукла вниз, то сложная функция ϕ(f(x)) является выпуклой вниз.

Доказательство. В силу выпуклости вниз f и возрастания ϕ, мы имеем

ϕ (f (qx1 + (1 − q)x2)) ≤ ϕ (qf(x1) + (1 − q)f(x2)) .

Далее, поскольку ϕ выпукла, находим

ϕ (qf(x1) + (1 − q)f(x2)) ≤ qϕ(f(x1)) + (1 − q)ϕ(f(x2)).

Сопоставляя данное неравенство с предыдущим, получаем нужное.

ТЕОРЕМА 2.4. Если y = f(x) и x = g(y) – однозначные, взаимно обратные функции (в соответствующих промежутках), то одновременно

Доказательство. Докажем первое из высказываний. Доказательства других утверждений предоставляются читателю. Пусть

f(qx1 + (1 − q)x2) ≤ qf(x1) + (1 − q)f(x2) = qy1 + (1 − q)y2.

По теореме об обратной функции, g также возрастает и g (qy1 + (1 − q)y2) ≥ g (f(qx1 + (1 − q)x2)) =

= qg(y1) + (1 − q)g(y2),

т.е. g – выпукла вверх.

ТЕОРЕМА 2.5. Выпуклая вниз в промежутке a, b функция f, f ≡const, не может достигать максимума внутри этого промежутка.

Доказательство. Предположим противное, т.е. функция достигает наибольшее значение во внутренней точке x0. Так как f ≡const, то можно заключить, что x1 < x0 < x2 и хотя бы на одном конце отрезка [x1, x2] значение функции строго меньше, чем в точке x0. Пусть, например

f(x1) < f(x0), f(x2) ≤ f(x0).

Положим x0 = qx1 + (1 − q)x2. Умножим обе части первого неравенства на q, а второго на (1 − q) и сложим их. Полученное неравенство

qf(x1) + (1 − q)f(x2) < f(x0) = f (qx1 + (1 − q)x2)

противоречит выпуклости вниз f.

ТЕОРЕМА 2.6. Если функция f выпукла вниз на промежутке a, b и отрезок [x1, x2], x1 < x2, содержится в a, b , то соотношение (1) выполняется либо всегда со знаком ”=” , либо всегда со знаком строгого неравенства.

Геометрически: дуга A1AA2 либо сливается с хордой A1A2, либо вся (за исключением концов) лежит под хордой.

Доказательство. Пусть

Тогда

ϕ(x) = f(x) − l(x) = f(x) + [−l(x)]

–выпукла вниз как сумма 2-х выпуклых вниз функций. Мы имеем ϕ(x1) = 0, ϕ(x2) = 0. Возможны варианты:

1)ϕ(x) ≡ 0 f(x) ≡ l(x), т.е. дуга сливается с хордой.

2)ϕ(x) < 0 x (x1, x2), поскольку в противном случае ϕ достигает максимума внутри [x1, x2], что невозможно. Отсюда, f(x) < l(x).

ОПРЕДЕЛЕНИЕ 2.1. Если для любого отрезка

[x1, x2] a, b соотношение (1) выполняется со знаком неравенства, f называется строго выпуклой вниз.

Определение строгой выпуклости вверх — аналогично.

УПРАЖНЕНИЕ 1. Доказать, что

§3. Условия выпуклости

Учитывая результаты предыдущего раздела, неравенство, определяющее выпуклую вниз функцию, можно переписать в виде

для x1 < x < x2. Следовательно,

(x2 − x)f(x1) + (x1 − x2)f(x) + (x − x1)f(x2) ≥ 0, (1)

Геометрический смысл:

Определитель в (2) равен удвоенной площади A1AA2.

ТЕОРЕМА 3.1. Предположим, что функция f определена и непрерывна на промежутке a, b и имеет в каждой точке конечную производную f . Для того чтобы f была выпуклой вниз на a, b , необходимо и достаточно, чтобы производная f неубывала.

Доказательство. Необходимость. Пусть x1 < x < x2. Перепишем неравенство (1) в виде

Последовательно устремляя здесь x → x1, x → x2, получаем

т.е. f (x1) ≤ f (x2).

Достаточность. Применим формулу конечных приращений

где x1 < ξ1 < x < ξ2 < x2. Так как f не убывает, то f (ξ1) ≤ f (ξ2) и мы приходим к соотношению (3).

148 Глава 7. Выпуклые функции

ТЕОРЕМА 3.2. Предположим, что f определена и непрерывна вместе со своей производной f на a, b , а также имеет на (a, b) конечную вторую производную f (x). Для выпуклости вниз (вверх) f на a, b необходимо

и достаточно, чтобы всюду на (a, b) вторая производная

f ≥ 0 (f ≤ 0).

Доказательство. Так как f > 0, то f неубывает. По предыдущей теореме получаем требуемое.

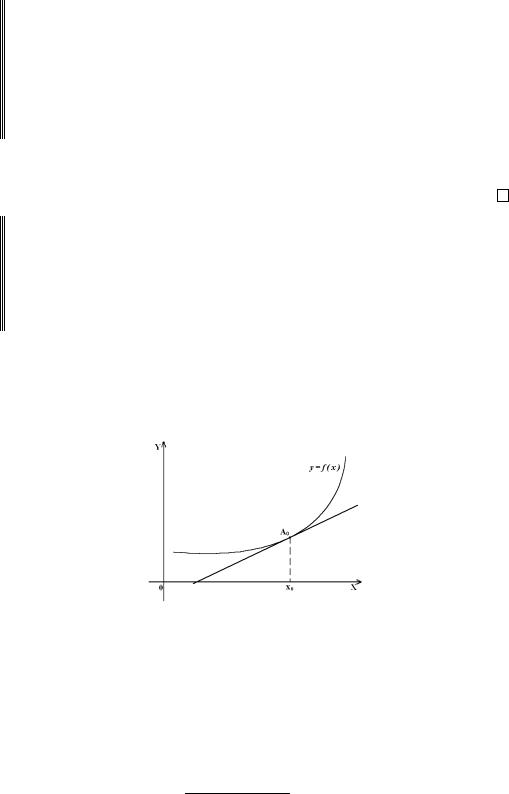
ТЕОРЕМА 3.3. Предположим, что f определена и непрерывна на (a, b) и имеет там конечную производную f . Для выпуклости вниз f необходимо и достаточно, чтобы ее график лежал над любой своей касательной (или на ней).

Доказательство. Необходимость. Уравнение касательной в точке A0 = (x0, f(x0)) имеет вид

y = f(x0) + f (x0)(x − x0).

Необходимо показать, что выпуклость вниз f влечет свойство: x0, x (a, b) выполнено

Данные соотношения совпадают с двойным неравенством (4) в теореме 3.1, если в левом из неравенств положить x2 = x, x1 = x0, а в правом – x2 = x0, x1 = x.

§5. Замечания о построении графика функции

Часто при изучении той или иной функции, достаточно ограничиться эскизом ее графика. Однако в ответственных случаях, требуется более подробное исследование. Имеется несколько отличающихся друг от друга схем построения графиков. Мы предлагаем здесь схему, заимствованную из "Сборника задач и упражнений по математическому анализу"

Б.П. Демидовича.

Для построения графика функции y = f(x) необходимо:

1.определить область существования данной функции и исследовать поведение функции в граничных точках последней;

2.выяснить симметрии графика, периодичность;

3.найти точки разрыва функции и промежутки непрерывности;

4.определить нули функции и области постоянства знака;

5.найти точки экстремума и описать промежутки возрастания и убывания функции;

6.определить точки перегиба и указать промежутки вогнутости определенного знака функции;

7.найти асимптоты в случае их существования;

8.указать те или иные специфические особенности графика.

Вчастных случаях общая схема упрощается. Полезно использовать простейшие преобразования графиков известных функций, такие как сдвиг, сжатие, растяжение, симметричное отображение, известные еще из школьного курса математики. Для более подробного изучения данной темы, мы можем рекомендовать книгу Р.Б. Райхмиста "Графики функций", в которой содержится достаточно большое количество полезных примеров.