Лосев-КлячинМиклюков МА в КИ

В точке же x = 0 производная существует:

§6. Правила вычисления производных

Пусть x (a, b) – произвольная точка.

ТЕОРЕМА 6.1. Предположим, что функция u = u(x) имеет в точке x производную u (x) и C ≡ const. Тогда функция Cu(x) также имеет производную в этой точке,

причем

(Cu) = Cu .

Доказательство. Действительно, как легко видеть,

ТЕОРЕМА 6.2. Предположим, что функции u и v имеют производные в x. Тогда функция y = u ± v также имеет производную в этой точке, причем

(u ± v) = u ± v .

Доказательство. Достаточно заметить, что для приращений функций u, v и ∆(u ± v) справедливо соотношение

∆(u ± v) = ∆u ± ∆ v,

или

∆1x∆(u ± v) = ∆∆xu ± ∆∆xv.

Переходя к пределу при ∆x → 0, получаем нужное.

ТЕОРЕМА 6.3. Предположим, что функции u и v имеют производные в x. Тогда функция y = u v также имеет производную в этой точке, причем

(u v) = u v + u v .

Доказательство. Здесь для доказательства достаточно заметить, что

∆ (u v) = u(x+∆x) v(x+∆x)−u(x) v(x) = u(x+∆x) v(x+∆x)−

−u(x + ∆x) v(x) + u(x + ∆x) v(x) − u(x) v(x) =

= u(x + ∆x) [v(x + ∆x) − v(x)] + [u(x + ∆x) − u(x)] v(x).

Разделив данное выражение на ∆x, и переходя к пределу при ∆x → 0, получаем нужное (Закончите доказательство самостоятельно!).

ТЕОРЕМА 6.4. Предположим, что функции u и v имеют производные в x, причем v(x) = 0. Тогда функция y = uv также имеет производную в этой точке и спра-

ведливо соотношение

u = u v − u v . v v2

Доказательство. Заметим, что

u(x + ∆x) = u(x) + u(x + ∆x) − u(x) =

= u + ∆u.

и, стало быть, справедливо равенство

Разделив данное выражение на ∆x, и переходя к пределу при ∆x → 0, получаем нужное (Закончите доказательство самостоятельно!).

УПРАЖНЕНИЕ 1. Доказать указанные свойства для общего случая производной fE(x) по множеству E R, имеющего x E своей точкой сгущения.

§7. Производная сложной функции

Пусть y = f(u) и u = ϕ(x) – функции, определенные на интервалах (c, d) и (a, b) соответственно, причем существует сложная функция y = f[ϕ(x)].

ТЕОРЕМА 7.1. Предположим, что u = ϕ(x) имеет в некоторой точке x0 (a, b) производную ϕ (x0), а функ-

ция y = f(u) имеет в точке u0 (c, d), u0 = ϕ(x0), производную f (u0). Тогда сложная функция y = f[ϕ(x)] также имеет производную в точке x0, причем

[f(ϕ(x))]x=x0 = f [ϕ(x0)] · ϕ (x0)

или, кратко,

yx = yu · ux (цепное правило).

Доказательство. Так как f дифференцируема в точке u0, то

∆y = yu · ∆u + α · ∆u,

где α(u) – некоторая бесконечно малая при u → u0.

УПРАЖНЕНИЕ 1. Пользуясь определением производной, докажите данную формулу.

Отсюда,

∆∆xy = yu · ∆∆ux + α · ∆∆ux.

Пользуясь непрерывностью ϕ в точке x0, замечаем, что u = ϕ(x) → u0 при x → x0, и, переходя к пределу при ∆x = x − x0 → 0, легко получаем нужное.

§8. Производные высших порядков. Формула Лейбница

Напомним, что если y = f(x) имеет конечную производ-

ную в X, то эта производная сама представляет собой новую функцию, которая может иметь производную. Ее называют

производной второго порядка. Обозначение: y , dxd2y2 , ...

Аналогично определяется производная третьего порядка, четвертого порядка и т.д. Таким образом,

y(n) = [y(n−1)] .

Заметим, что из предположения, что функция f имеет в точке a производную порядка n, следует, в силу определения последней, что в некоторой окрестности точки a существует производная порядка n − 1, а, следовательно, при n > 1 и все производные более низкого порядка k < n − 1. При этом все производные, порядок которых меньше n, непрерывны в указанной окрестности (что следует из теоремы о связи дифференцируемости и непрерывности).

ОПРЕДЕЛЕНИЕ 8.1. Функция называется n раз непрерывно дифференцируемой на некотором промежутке, если во всех точках этого промежутка она имеет непрерывные производные до порядка n включительно (n = 0, 1, . . .).

УПРАЖНЕНИЕ 1. Доказать, что приведенное выше определение эквивалентно следующему:

Функция называется n раз непрерывно дифференцируемой на некотором промежутке, если во всех точках этого промежутка она имеет непрерывную производную порядка n.

Рассмотрим несколько примеров. Очевидно, что

(Cu)(n) = Cu(n), (u ± v)(n) = u(n) ± v(n).

ПРИМЕР 1. Вычислим производную n-го порядка функции y = sin x. Имеем

y = cos x, y = − sin x, y = − cos x, y(4) = sin x, ... .

sin(n) x = sin(x + nπ2 ).

ПРИМЕР 2. Пусть функции u и v имеют производные n-го порядка. Вычислим n-ю производную функции y = uv. Мы последовательно находим

y = u v + v u,

y = u v + 2u v + uv ,

y = u v + 3u v + 3u v + uv ,

n

y(n) = (uv)(n) = Cni u(n−i)v(i). i=0

Последнее доказывается методом математической индукции. При n = 1 равенство верно. Предположим, что оно верно для производной порядка n. Тогда

n

y(n+1) = Cni [u(n−i)v(i)] = i=0

Учитывая, что Cnk + Cnk−1 = Cnk+1 (докажите!), получаем требуемое, т.е.

Тогда

(x2 cos ax)(50) = −a50x2 cos ax−100a49x sin ax+2450a48 cos ax.

ПРИМЕР 4. Многочлены Лежандра1 суть выражения вида

где постоянным Cn придаются те или иные значения из соображений удобства.

Убедимся, что многочлен Xn(x) имеет n различных вещественных корней, которые все содержатся между −1 и 1. Для простоты пусть Cn = 1. Тогда

(x2 − 1)n = (x − 1)n(x + 1)n.

Заметим, что (n −1)–последовательная производная обраща-

1Лежандр Адриен Мари (18.9.1752-10.1.1833). Род. в Париже (Франция). Член Парижской АН (1785). Ему принадлежит ряд значительных результатов в теории геодезических измерений, математическом анализе, теории чисел.

Все слагаемые, начиная со второго, содержат множитель (x − 1) и обращаются в 0 при x = 1, откуда следует, что

Xn(1) = 2nn!.

Аналогично,

Xn(−1) = (−1)n2nn!.

Положим теперь Cn = 2n1n! (чаще всего так и делают). Обозначим полученный многочлен через Pn(x). Имеем

Pn(1) = 1, Pn(−1) = (−1)n.

С помощью формулы Лейбница2 легко установить, что

(x2 − 1)Xn + 2xXn − n(n + 1)Xn = 0.

Действительно, y = (x2 − 1)n и, далее,

y = 2nx(x2 − 1)n−1 = (x2 − 1)y = 2nxy.

Возьмем (n + 1)-e производные от обеих частей последнего равенства. По формуле Лейбница имеем

(x2 − 1)y(n+2) + (n + 1)2xy(n+1) + n(n + 1)2y(n) = 2nxy(n+1)+ 2

+(n + 1)2ny(n) = (x2 −1)y(n+2) + 2xy(n+1) −n(n + 1)y(n) = 0.

Умножая на Cn, получаем требуемое.

§9. Производная функции, заданной в параметрическом виде. Логарифмическая производная

Пусть x = ϕ(t), y = ψ(t) – функции, определенные на (a, b), причем x = ϕ(t) имеет обратную функцию t = Θ(x). Предположим, что ϕ и ψ имеют производные в точке t0 (a, b). Пусть x0 = ϕ(t0). Так как

f (x0) = ψt(t0) · Θ (x0).

2Лейбниц Готфрид Вильгельм (1.7.1646-14.11.1716) – математик, философ и теолог. Род. в Лейпциге (Германия). Организатор и первый президент Берлинской АН (1700), член Лондонского королевского общества (1673), член Парижской АН (1700). Один из основателей дифференциального и интегрального исчислений.

Заметим, впрочем, что можно сразу воспользоваться форму-

лой

uv = e(v ln u).

§10. Дифференциал

ОПРЕДЕЛЕНИЕ 10.1. Предположим, что функция

y = f(x) определена на (a, b) и x0 (a, b) – некоторая точка. Если при x − x0 = ∆x → 0 выполнено

где A – подходящая постоянная, то говорят, что f является дифференцируемой в точке x0; само же выражение A∆x называется дифференциалом функции и обозначается символом dy или df(x0).

Дифференциал аргумента dx по определению равен ∆x.

Равенство (1) показывает, что бесконечно малые ∆y и A∆x эквивалентны при ∆x → 0. Другими словами, величина A∆x является главной линейной частью бесконечно малой ∆y, если за основную бесконечно малую принята ∆x.

ТЕОРЕМА 10.1. Для того чтобы функция y = f(x) имела дифференциал в точке x0, необходимо и достаточно, чтобы в этой точке существовала конечная производная y = f (x0). При выполнении этого условия

Доказательство. Необходимость. Предположим, что выполнено (1). Тогда

∆∆fx = A + o(∆∆xx).

Следовательно, существует предел

A = lim ∆y = f (x0).

∆x→0 ∆x

Для доказательства (2) достаточно заметить, что

dy = A∆x = f (x0)dx.

Достаточность. Так как производная f (x0) существует, то

Рассмотрим независимую переменную x. Так как dx = ∆x,

то соотношение df = f (x0)dx влечет f (x0) = dxdf , то есть выражение, которое ранее рассматривалось в качестве цельного

символа, можно рассматривать как дробь.

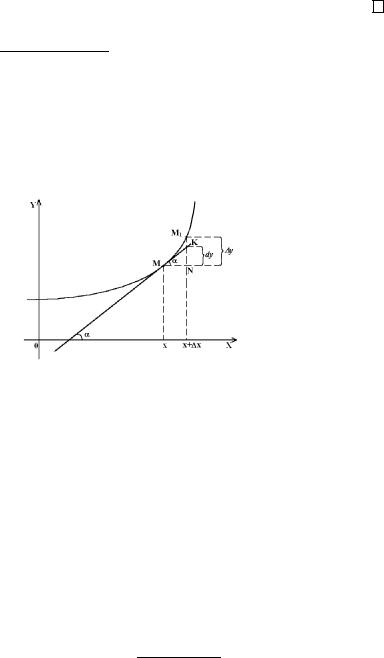
Геометрический смысл дифференциала

Обозначим через ∆y приращение ординаты кривой, а через dy – приращение ординаты касательной.

Дифференциал функции в точке – это приближение приращения функции в окрестности точки линейной функцией с точностью до бесконечно малой порядка выше единицы.

Основные формулы для дифференциалов получаются из

соответствующих формул для производных.

Правила дифференцирования:

Иногда дифференциал весьма удобно использовать для приближенных вычислений.

ПРИМЕР 1. Вычислим приближенно 0, 982. Мы имеем

0, 982 = (1−0, 02)2 = 12 −2·1·0, 02+0, 022 ≈ 1−0, 04 = 0, 96.

110 Глава 4. Производная

ПРИМЕР 2. Вычислим проближенно ln 0, 98. Полагая ∆y ≈ dy и пользуясь (2), можем записать

∆y ≈ y (x0)∆x,

т.е.

1

ln(x0 + ∆x) − ln x0 ≈ x0 · ∆x.

Таким образом, полагая x0 = 1 и ∆x = 0, 02, находим

ln 0, 98 = ln(1 − 0, 02) − ln 1 ≈ 11 · (−0, 02) = −0, 02.

§11. Дифференциалы высших порядков. Инвариантность формы первого дифференциала

В данном параграфе для обозначения дифференциала наряду с символом d мы будем использовать символ δ, там, где это будет удобно.

Предположим, что функция y = f(x) дифференцируема в некоторой окрестности точки x0. Тогда первый дифференциал этой функции dy = f (x)dx является функцией двух переменных: точки x и величины dx. Предположим дополнительно, что функция f (x) также является дифференцируемой в точке x0 и, что величина dx является постоянной для всех точек x рассматриваемой окрестности точки x0. При этих предположениях существует дифференциал функции dy = f (x)dx в точке x0, который пока мы будем обозначать δ(dy). Более того, справедливы следующие рассуждения.

ОПРЕДЕЛЕНИЕ 11.1. Значение δ(dy) дифференциала от первого дифференциала dy, взятое при δx = dx, называют вторым дифференциалом функции y = f(x) (в точке x0) и

обозначают символом d2y.

Из определения и формулы (1) следует, что

d2y = f (x0)(dx)2.

Аналогично, по индукции, определяются дифференциалы более высоких порядков.