Лосев-КлячинМиклюков МА в КИ

ТЕОРЕМА 9.1. Предположим, что функция F дифференцируема всюду на (−∞, +∞) и удовлетворяет там условию (1). Тогда

i)существует и единственен корень ξ уравнения (2);

ii)итерационная последовательность {xn}, описываемая равенством (3), сходится к ξ при любом выборе начальной точки x0;

iii)для любого n > 1 выполнено

Доказательство. Прежде всего заметим, что итерационная последовательность {xn} фундаментальна. Действительно, фиксируем произвольно ε > 0. Так как q < 1, то существует номер N(ε) такой, что при всех n > N(ε) выполнено

qn |x1 − x0| < ε.

1 − q

Таким образом, для любых m > n > N(ε), в силу (5), имеем

|xm − xn| ≤ qn |x1 − x0| < ε,

1 − q

что и требуется.

Поскольку последовательность {xn} фундаментальна, то на основании критерия Коши она сходится. Обозначим ее предел через ξ. Так как F дифференцируема, то она непрерывна, и потому из (3) вытекает

ξ = lim xn+1 = lim F (xn) = F (ξ),

n→∞ n→∞

т.е. число ξ является корнем уравнения (2).

Докажем, что этот корень является единственным. Предположим противное, т.е. для некоторого η = ξ также выполнено F (η) = η. Не умаляя общности, можем считать, что ξ < η. Согласно формуле конечных приращений Лагранжа,

имеем

0 < η − ξ = F (η) − F (ξ) = F (c)(η − ξ),

где c (ξ, η) – некоторая точка. Отсюда, в силу условия (1), находим

|η − ξ| ≤ |F (c)||η − ξ| ≤ q|η − ξ|.

Противоречие с предположением 0 < q < 1.

Имеются модификации метода, пригодные для вычисления корня уравнения (2) в случае, когда F задана на конечном отрезке [a, b]. См., например, В.А. Ильин и Э.Г. Позняк, Основы математического анализа, часть I, стр. 392.

9.2.Метод касательных

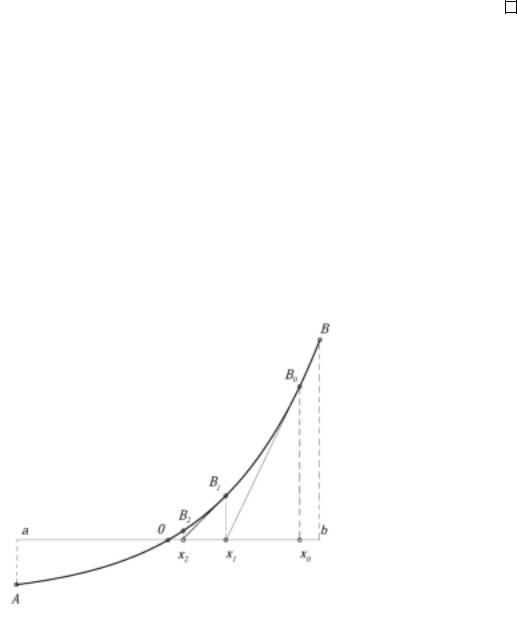
Предположим, что уравнение F (x) = 0 имеет корень ξ на отрезке [a, b]. Воспользуемся следующим алгоритмом для приближенного нахождения корня.

Пусть: x0 – произвольная начальная точка;

x1 – точка пересечения касательной к графику F в точке x0 с осью ox;

x2 – точка пересечения касательной к графику F в точке x1 с осью ox;

...............................................................................

xn – точка пересечения касательной к графику F в точке xn−1 с осью ox.

Найдем итерационную формулу. Уравнение касательной, проходящей через точку xn−1, имеет вид

y = F (xn−1)(x − xn−1) + F (xn−1).

Тем самым, точка пересечения этой касательной с осью y = 0, т.е. точка xn определяется по формуле

F (xn−1) xn = xn−1 − F (xn−1).

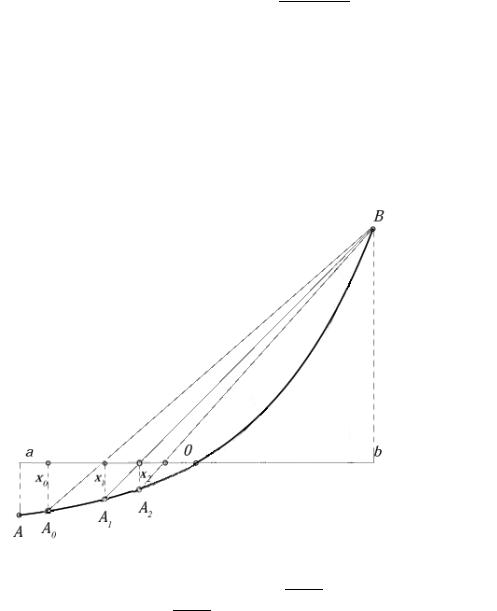
9.3.Метод хорд

Предположим, что уравнение F (x) = 0 имеет корень ξ на отрезке [a, b].

Описание метода: x0 [a, b] – произвольная начальная точ-

ка; x1 – точка пересечения хорды A0B с осью y = 0; x2 – точка

пересечения хорды A1B с осью y = 0 и т.д.

УПРАЖНЕНИЕ 1. Обоснования методов касательных и хорд посмотреть самостоятельно (например, в книге В.А. Ильина и Э.Г. Позняка, Основы математического анализа, часть I, стр. 393-398).

Глава 6

Формула Тейлора

§1. Производные многочлена и его разложение по степеням

ТЕОРЕМА 1.1. Пусть P (x) = n ckxk – произволь-

k=0

ный многочлен степени n. Пусть a R – произвольная точка. Тогда

ЗАМЕЧАНИЕ. Здесь P (k)(a) – значение производной k-го порядка в точке a при k = 1, 2, ..., n. При k = 0 – значение самой функции.

Доказательство. Произведя замену x = (x − a) + a в многочлене P (x), получаем

n

P (x) = ck[(x − a) + a]k,

k=0

что, как легко видеть, можно переписать в виде

P (x) = d0 + d1(x − a) + d2(x − a)2 + ... + dn(x − a)n. (2)

Найдем коэффициенты d0, d1, ..., dn. Подставляя в обе части

(2) x = a, имеем

P (a) = d0.

Дифференцируя равенство (2) по x, приходим к соотношению

P (x) = d1 + 2d2(x−a) + ...+ kdk(x−a)k−1 + ...+ ndn(x−a)n−1

и при x = a получаем

P (a) = d1.

Предположим, что функция f имеет в точке x = a все производные вплоть до порядка n. По образцу многочлена (1) составим многочлен

Данный многочлен называется многочленом Тейлора1 для функции f (с центром в точке a и степени n).

ТЕОРЕМА 2.1. Если f имеет в точке x = a производную порядка n, то

Доказательство. Положим

ϕ(x) = f(x) − Tn(x).

Функция ϕ дифференцируема n раз, причем

ϕ(a) = ϕ (a) = ... = ϕ(n)(a) = 0.

Покажем, что отсюда вытекает свойство

ϕ(x) = o((x − a)n) при x → a

или, что то же самое,

ϕ(x) = ε(x)(x − a)n,

где ε(x) → 0 при x → a.

Воспользуемся методом математической индукции. Утверждение справедливо при n = 1, поскольку из равенства

ϕ(a) = ϕ (a) = 0

и формулы

ϕ(x) − ϕ(a) = ϕ (a)(x − a) + o(x − a) при x → a

следует, что ϕ(x) = o(x − a) (x → a).

Предположим, что данное высказывание верно для n = k, и покажем, что оно верно при n = k + 1. Итак, пусть

ϕ(a) = ϕ (a) = ... = ϕ(k+1)(a) = 0.

Тогда производная ϕ дифференцируема k раз в точке x = a и, по предположению индукции, для нее выполнено

1Тейлор Брук (18.8.1685-29.12.1731) – математик и философ. Род. в Эдмонтоне (Англия). Член Лондонского королевского общества.

Однако, по формуле Лагранжа,

ϕ(x) = ϕ(x) − ϕ(a) = ϕ (ξ)(x − a),

где ξ точка, заключенная между a и x, и ξ → a при x → a. Поэтому из (4) получаем

ϕ(x) = ϕ (ξ)(x − a) = ε(ξ)(ξ − a)k(x − a) =

где ε1(x) → 0 при x → 0. Последнее равенство является следствием того, что точка ξ находится между точками a и x, а также неравенства

ЗАМЕЧАНИЕ. Формула (3) может быть записана в виде

Величина o((x−a)n) имеет смысл остаточного члена. Формула (5) называется формулой Тейлора с остаточным членом в форме Пеано2. В частном случае для n = 1 мы имеем

f(x) = f(a) + f (a)(x − a) + o(x − a) при x → a,

т.е. уже известную нам формулу.

ТЕОРЕМА 2.2. Если f имеет производную порядка n в

точке x = a и существует многочлен Pn(x) = c0 + c1x + ... + cnxn, для которого

то Pn = Tn, то есть является многочленом Тейлора с центром в точке a.

Доказательство. Согласно теореме 2.1 имеем

f(x) = Tn(x) + o((x − a)n)

2Пеано Джузеппе (27.8.1858, Кунео, – 20.4.1932, Турин), итальянский математик. С 1890 профессор Туринского университета (Италия). Занимался изучением основных понятий и фактов анализа (вопрос о возможно более широких условиях существования решения дифференциальных уравнений, определение и содержание понятия кривой) и формально-логическим обоснованием математики. Во всеобщее употребление вошла его аксиоматика натурального ряда чисел. Первым построил пример непрерывной кривой, целиком заполняющей некоторый квадрат (1890 г.).

и поэтому из (6) получаем

Tn(x) − Pn(x) = o((x − a)n) − o((x − a)n) = o((x − a)n).

Учитывая, что многочлен Pn можно записать в виде (1), находим

Подставляя в это равенство x = a, получаем

f(a) = f(0)(a) = Pn(a).

Следовательно, нулевые члены в суммах в (6) взаимно уничтожаются и мы получим

Pn(x) = Tn(x).

§3. Формула Тейлора с остаточным членом в форме Лагранжа и в форме Коши

Величина Rn(x) = f(x) − Tn(x) называется остаточным членом в формуле Тейлора. Ранее мы показали, что если f имеет в точке x = a производную порядка n, то Rn(x) = o((x − a)n) при x → a. Однако зачастую данной информации об остаточном члене бывает слишком мало, поскольку никаких границ для величины o((x − a)n) при этом