
Лосев-КлячинМиклюков МА в КИ
.pdfСодержание |
|
11 |
|
§8 |
Интеграл Эйлера первого рода . . . . . . . . . |
454 |
|
§9 |
Интеграл Эйлера второго рода . . . . . . . . . |
457 |
|
19 Преобразование Фурье |
464 |
||
§1 Основные определения . . . . . . . . . . . . . . |
464 |
||
§2 Условие представимости функции интегралом |
471 |
||
|
Фурье . . . . . . . . . . . . . . . . . . . . . . . |
||
§3 Гладкость функции и скорость убывания ее пре- |
476 |
||
|
образования Фурье . . . . . . . . . . . . . . . . |
||
§4 Пространство быстро убывающих функций . . |
479 |
||
|
4.1 |
Пространство S . . . . . . . . . . . . . . |
479 |
|
4.2 |
Понятие оператора . . . . . . . . . . . . |
480 |
|
4.3 |
Преобразование Фурье как оператор . . |
482 |
§5 |
Обратный оператор Фурье . . . . . . . . . . . |
484 |
|
§6 |
Свертка и ее преобразование Фурье . . . . . . |
486 |
|
§7 |
Пространство S обобщенных функций . . . . |
488 |
|
7.1Понятие обобщенной функции . . . . . 488
7.2Кусочно непрерывные функции как обоб-
щенные . . . . . . . . . . . . . . . . . . 489
7.3δ-функция Дирака . . . . . . . . . . . . 492
§8 Операции над обобщенными функциями . . . 493
8.1Умножение на функцию . . . . . . . . . 493
8.2Определение производной обобщенной функции . . . . . . . . . . . . . . . . . . . . . 493
8.3 |
Производная функции Хевисайда . . . |
494 |
8.4 |
Сходимость в пространстве обобщенных |
494 |
|
функций . . . . . . . . . . . . . . . . . . |
|
§9 Сжатие видеоинформации . . . . . . . . . . . . |
496 |
|
20 Теория интегрирования в Rn |
498 |
|
§1 Интеграл по параллелепипеду . . . . . . . . . |
498 |
|
1.1Определение и простейшие свойства . . 498
1.2Условие интегрируемости . . . . . . . . 503 §2 Интегрирование по множеству . . . . . . . . . 506
2.1Множества, измеримые по Жордану . . 506
|
2.2 |
Интеграл по произвольному множеству |
507 |
|
2.3 |
Свойства интеграла по множеству . . . |
510 |
§3 |
Сведение кратного интеграла к повторному . . |
513 |
|
|
3.1 |
Случай параллелепипеда . . . . . . . . |
513 |
|
3.2 |
Случай произвольного множества . . . |
516 |
§4 |
Понятие о несобственном кратном интеграле . |
520 |
|
§5 |
Теорема о среднем . . . . . . . . . . . . . . . . |
523 |
|
§6 |
Криволинейные интегралы . . . . . . . . . . . |
524 |
|
6.1Криволинейный интеграл I рода . . . . 524
6.2Криволинейный интеграл II рода . . . . 527
6.3Криволинейный интеграл по замкнуто-
му контуру . . . . . . . . . . . . . . . . 530
12 |
Содержание |
6.4Связь между криволинейными интегралами I и II рода . . . . . . . . . . . . . . 534
6.5Формула Грина . . . . . . . . . . . . . . 535
§7 |
Приложения интеграла . . . . . . . . . . . . . |
541 |
|
§8 |
Площадь в криволинейных координатах . . . . |
543 |
|
§9 |
Замена переменных в кратном интеграле . . . |
547 |
|
§10 |
Векторные поля . . . . . . . . . . . . . . . . . |
549 |
|
|
10.1 |
Потенциальные векторные поля . . . . |
549 |
§11 |
10.2 |
Точный дифференциал . . . . . . . . . |
554 |
Понятие площади поверхности . . . . . . . . . |
557 |
||
11.1Площадь поверхности, заданной графиком функции . . . . . . . . . . . . . . . 557
11.2Площадь поверхности, заданной параметрически . . . . . . . . . . . . . . . . . . 559
11.3 Пример Шварца . . . . . . . . . . . . . |
561 |
§12 Поверхностные интегралы . . . . . . . . . . . . |
563 |
12.1Поверхностный интеграл I рода . . . . . 563
12.2Ориентация поверхности . . . . . . . . . 566
12.3Интеграл по ориентированной плоской
области . . . . . . . . . . . . . . . . . . 568
12.4Поверхностный интеграл II рода . . . . 570
12.5Формула Гаусса-Остроградского . . . . 573
12.6Геометрический смысл дивергенции . . 577
12.7 |
Формула Стокса . . . . . . . . . . . . . |
578 |
12.8 |
Геометрический смысл ротора . . . . . |
582 |
12.9Соленоидальные векторные поля . . . . 583
21 Внешние дифференциальные формы |
585 |
§1 Определение внешней формы . . . . . . . . . . |
585 |
1.1Основные понятия . . . . . . . . . . . . 585
1.2Сложение и умножение на функцию . . 587 §2 Внешнее умножение форм . . . . . . . . . . . . 588
2.1Сигнатура перестановки . . . . . . . . . 588
2.2Внешнее произведение базисных форм . 588
2.3Определение операции умножения . . . 589
2.4Свойства операции умножения . . . . . 590
2.5Следствия . . . . . . . . . . . . . . . . . 593 §3 Внешнее дифференцирование . . . . . . . . . . 594
|
3.1 |
Понятие внешнего дифференцирования |
594 |
|
3.2 |
Примеры . . . . . . . . . . . . . . . . . |
595 |
§4 |
3.3 |
Свойства операции дифференцирования |
596 |
Первая теорема Пуанкаре . . . . . . . . . . . . |
598 |
||
§5 |
Индуцированное отображение форм . . . . . . |
599 |
|
§6 |
Вторая теорема Пуанкаре . . . . . . . . . . . . |
603 |
|
6.1Диффеоморфизмы и их свойства . . . . 603
6.2Формулировка теоремы . . . . . . . . . 604
6.3 |
Замкнутые и точные формы . . . . . . |
604 |
6.4 |
Иллюстрирующие примеры . . . . . . . |
605 |
Содержание |
|
13 |
6.5 |
Доказательство теоремы . . . . . . . . . |
606 |
§7 Поверхности в Rn . . . . . . . . . . . . . . . . . |
610 |
|
7.1Вложения и погружения . . . . . . . . . 610
7.2 |
Локальная карта и атлас . . . . . . . . 611 |
7.3Ориентация . . . . . . . . . . . . . . . . 613
7.4Поверхности с краем . . . . . . . . . . . 615
7.5Кусочно-гладкие поверхности . . . . . . 618
7.6Теорема о разбиении единицы . . . . . . 619
7.7Доказательство теоремы . . . . . . . . . 622
7.8Следствия . . . . . . . . . . . . . . . . . 625 §8 Внешние формы на поверхности . . . . . . . . 627
8.1Определение формы на поверхности . . 627
8.2Интеграл от формы по поверхности . . 628
8.3Форма объема поверхности . . . . . . . 629
8.4 |
Формула Стокса . . . . . . . . . . . . . |
632 |
22 Добавление 1. Элементы теории множеств и |
||
метрических пространств |
634 |
|
§1 Сравнение множеств . . . . . . . . . . . . . . . |
634 |
|
1.1Эквивалентность множеств. Мощность множества . . . . . . . . . . . . . . . . . . . 634
1.2 |
Счетные множества . . . . . . . . . . . 635 |
1.3Мощность континуума . . . . . . . . . . 638
1.4Критерий эквивалентности множеств . 639
1.5Сравнение мощностей . . . . . . . . . . 640
§2 Метрические пространства . . . . . . . . . . . 642
2.1Точки прикосновения. Замыкание . . . 642
2.2Сходимость в метрическом пространстве 645
2.3Плотные подмножества. Сепарабельность 645
2.4Простейшие свойства замкнутых и от-
крытых множеств . . . . . . . . . . . . 646
2.5Строение открытых и замкнутых подмножеств прямой . . . . . . . . . . . . . 648
2.6Канторово множество . . . . . . . . . . 649
2.7Замечания о двоичных дробях . . . . . 651 §3 Покрытия. Размерности. Фракталы . . . . . . 652
3.1Покрытия множеств . . . . . . . . . . . 652
3.2Размерность по Минковскому . . . . . . 658
3.3Мера и размерность по Хаусдорфу. Понятие фрактала . . . . . . . . . . . . . . 659
3.4 |
Кривая Коха . . . . . . . . . . . . . . . 662 |
3.5Ковер Серпинского . . . . . . . . . . . . 662
3.6Фрактальные принципы в литературных текстах . . . . . . . . . . . . . . . . . . . 663
§4 Полные метрические пространства . . . . . . . 663
4.1Определение и примеры полных метрических пространств . . . . . . . . . . . . 663
4.2Принцип вложенных шаров . . . . . . . 666
14 |
Содержание |
4.3Свойства полного метрического простран-
ства . . . . . . . . . . . . . . . . . . . . 667
4.4Пополнение пространства . . . . . . . . 668
4.5Множество R как пополнение множества рациональных чисел . . . . . . . . . . . 671
4.6Принцип "сжатых" отображений . . . . 672
23 |
Добавление 2. |
Неравенства Юнга, Гельдера, |
||
|
Минковского |
|
675 |
|
24 |
Добавление 3. |
Еще раз о рядах |
678 |
|
|
§1 |
Расходящиеся ряды . . . . . . . . . . . . . . . |
678 |
|
|
§2 |
Обвертывающие ряды . . . . . . . . . . . . . . |
682 |
|
|
§3 |
Разложение по собственным функциям . . . . |
684 |
|
|
§4 |
Всплески (вэйвлеты) . . . . . . . . . . . . . . . |
686 |
|
25 Добавление 4. Обработка результатов эксперимента 690
§1 Сплайны . . . . . . . . . . . . . . . . . . . . . . 690
1.1Понятие сплайна . . . . . . . . . . . . . 690
1.2Интерполяционные эрмитовы сплайны . 692
1.3Кубические интерполяционные сплайны 694
1.4Экстремальные свойства кубических
1.5 |
интерполяционных сплайнов . . . . . . |
696 |
Замечание о двумерных сплайнах . . . |
698 |
|
§2 Замечания о других методах . . . . . . . . . . |
699 |
|
2.1Дискриминантный анализ . . . . . . . . 699
2.2Кластерный анализ . . . . . . . . . . . . 700
2.3Факторный анализ . . . . . . . . . . . . 700
26 Добавление 5. Практикум вычисления неопре-
деленных интегралов |
702 |
|
27 Добавление 6. Примеры и контрпримеры в тео- |
||
рии рядов и интегралов |
727 |
|
§1 |
Иллюстрирующие примеры. Числовые ряды . |
727 |
§2 |
Иллюстрирующие примеры. Функциональные |
730 |
§3 |
последовательности и ряды . . . . . . . . . . . |
|
Иллюстрирующие примеры. Несобственные |
731 |
|
|
интегралы . . . . . . . . . . . . . . . . . . . . . |
|
§4 Иллюстрирующие примеры. Интегралы, зави- |
732 |
|
§5 |
сящие от параметра . . . . . . . . . . . . . . . |
|
Важнейшие контрпримеры . . . . . . . . . . . |
733 |
|
28 Добавление 7. Примерная рабочая программа737
Авторский и предметный указатель . . . . . . . . . 747
Предисловие
Предлагаемое учебное пособие готовилось в течение нескольких лет, и в результате первая его часть является третьим изданием, вторая часть - вторым изданием, а последняя издается впервые. Мы попытались в максимально "мягком режиме" дать сжатое изложение введения в анализ, построенное по "концентрическому принципу" и предполагающее обращение к одним и тем же базовым понятиям (функция, производная, интеграл и т.п.) по несколько раз по мере того, как усложняется излагаемый материал. Тем самым существенно расширяется круг потенциальных читателей, которыми могут быть как студенты математического факультета, так и студенты, желающие получить инженерно-техническое и инженерно-экономическое образование.
Как обычно, теоретические тексты снабжены упражнениями, тестирующими уровень усвоения. Вместе с тем некоторые из упражнений требуют от читателя выхода за пределы материала, а в некоторых случаях и даже за пределы математики. Научиться давать мотивированные ответы на недостаточно точно (с точки зрения формальной логики) формулируемые вопросы — важная составная часть университетского математического образования.
Мы снабжаем основной курс математического анализа несколькими добавлениями. Во-первых, это — раздел, посвященный элементам теории множеств и метрических пространств. Для студентов-математиков важно познакомиться (пусть поверхностно!) с данными понятиями как можно ранее, чтобы быть готовым к встрече с (весьма формализованным) функциональным анализом. Студентам нематематических специальностей полезно хотя бы "краем уха" услышать о таких фундаментальных понятиях математики, как "счетные множества", "мощность континуума", "канторовы множества", "фракталы". Во-вторых, это — весьма часто встречающиеся в различных разделах математики неравенства Юнга, Гельдера и Минковского. В третьих, это — раздел, посвященный расходящимся рядам, обвертывающим рядам, разложениям по собственным функциям и вэйвлетам. В четвертых, это — раздел, посвященный обработке результатов экспериментов. Также это — практикум по вычислению неопределенных интегралов, полезный при выполнении домашних заданий, примеры и контрпримеры из теории рядов и интегралов, а также примерная рабочая программа курса.
Мы пытались изложить необходимый материал весьма сжато, в частности, широко используя логические символы , , →. Хотя, кажется, не без издержек и иногда в ущерб эстетическим принципам оформления текста. Вместе с тем сделать пособие приемлемым по цене — весьма непростая задача.
Авторы благодарны коллегам по Волгоградскому государственному университету, прочитавшим учебник в рукописи и сделавшим ряд замечаний, способствовавших улучшению текста. Также авторы считают своим долгом выразить благодарность студентам математического факультета ВолГУ, которые своими замечаниями способствовали улучшению качества второго издания пособия.

Глава 1
Предел последовательности
§1. Множества и операции над ними
Строго говоря, множеству нельзя дать точного определения. Обычно говорят, что множество — это собрание, совокупность, класс вещей, объединенных по какому-либо признаку. Однако, сказанное не может служить строгим математическим определением, поскольку опирается на понятия, не определенные ранее.1
Предметы, составляющие данное множество, называются его элементами. Запись a A означает, что a – элемент множества A. Множество, состоящее из конечного числа элементов, называется конечным. В противном случае – бесконечным. Множество, не содержащее ни одного элемента, называется пустым и обозначается символом .
Будем говорить, что два множества A и B совпадают (равны), и писать A = B, если они содержат одни и те же элементы, т.е. если каждый элемент x A является одновременно элементом множества B, и обратно, каждый элемент x B является одновременно элементом множества A.
Будем говорить, что множество A содержится в множестве B, и писать A B, если каждый элемент x A является одновременно элементом множества B. Множество A называется в этом случае подмножеством B.
Пересечение множеств A и B — это множество A∩B = {x : x A и x B} , т.е. множество всех x таких, что x принадлежит A и, одновременно, x принадлежит B.
1Действительно, в свою очередь, «собрание» — это «множество, совокупность, класс» вещей ... и т.д.
§1. Множества и операции над ними |
|
17 |
|
A |
|
|
|
|
|
|
|
A ∩ B
B
Объединением (суммой) двух множеств A и B называется
множество A |
|
B = {x : x A или |
|
x B} , т.е. множе- |
||||||||
|
всевозможных x, таких, что x |
|
|
A либо x |
B. |
|||||||
ство |
|
|
|
A |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A B |
|||
|
|
|
|
B |
|
|
|
|
|
|||
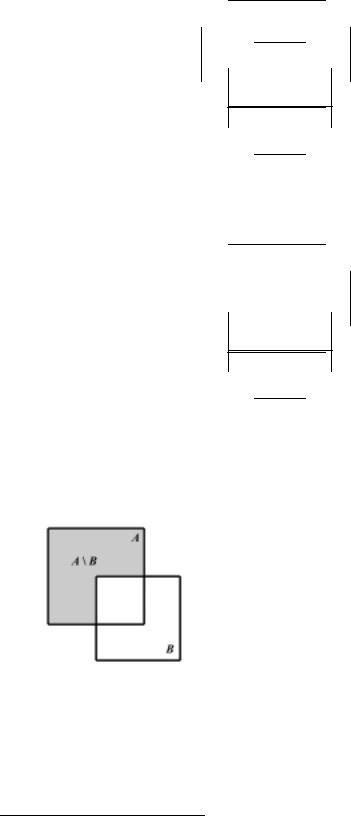
Разностью |
множеств A и B |
|
называется |
множество |
||||||||
A\B = {x A : и x B}.
Разность между множеством M и содержащимся в нем подмножеством A называют дополнением A в M и обозначают CM A или CA.
УПРАЖНЕНИЕ 1. Докажите следующие соотношения (так называемые правила де Моргана2):
CM (A B) = CM A ∩ CM B,
2Морган де Огастес (27.6.1806–18.3.1871) – шотландский математик и логик. Первый президент Лондонского математического общества. Он был одним из основателей формальной алгебры.
(Здесь и ниже, биографические данные взяты авторами из книги: А.И.Бородин, А.С.Бугай "Биографический словарь деятелей в области математики", К.: Радяньска школа, 1979.)
18 |
Глава 1. Предел последовательности |
CM (A ∩ B) = CM A CM B.
§2. Множества на числовой прямой
Множество элементов R называется множеством действительных чисел, если оно обладает перечисленными ниже свойствами.
I. Аксиомы сложения.
Для каждой пары a, b R существует элемент c R, называемый их суммой и обозначаемый a + b. При этом операция сложения такова, что:
1.a + b = b + a (коммутативность);
2.a + (b + c) = (a + b) + c (ассоциативность);
3.в множестве R существует элемент, обозначаемый символом 0 и такой, что для всякого элемента a R
выполнено a + 0 = a (аксиома существования
нуля);
4. для любого a R найдется b R, для которого a + b = 0; этот элемент обозначается символом −a и называется элементом, противоположным a.
II. Аксиомы умножения.
Для каждой пары a, b R определен элемент c R, называемый их произведением и обозначаемый a · b (или ab). При этом операция умножения такова, что:
1.a · b = b · a (коммутативность);
2.a · (b · c) = (a · b) · c (ассоциативность);
3.(a + b) · c = a · c + b · c (дистрибутивность);
4.в множестве R\{0} существует элемент, обозначаемый символом 1, такой, что a R выполнено a · 1 = a;
5.для всякого a R, a = 0, найдется b R такой,
что a · b = 1. Этот элемент обозначается a1 (или a−1)
иназывается обратным к элементу a.
III. Аксиомы порядка.
В множестве R определено понятие неравенства так, что для любых двух различных элементов a, b R выполнено одно и только одно из соотношений: либо a < b, либо b < a. При этом отношение неравенства обладает следующими свойствами:
1.Если a < b и b < c, то a < c (транзитивность).
2.Если a < b, то a + c < b + c, c R.
3.Если 0 < a и 0 < b, то 0 < ab.
ЗАМЕЧАНИЕ. Если a < b или a = b, т.е. если элемент a не превосходит элемента b, то пишут a ≤ b.
§2. Множества на числовой прямой |
19 |
IV. Аксиома полноты.
Зададим произвольно два непустых множества A и B из R. Если для любых двух элементов a A и b B выполнено a ≤ b, то существует элемент c R такой, что
a ≤ c ≤ b, a A, b B .
ЗАМЕЧАНИЕ. Множество Q всех рациональных чисел удовлетворяет всем перечисленным аксиомам, кроме аксиомы полноты, называемой также аксиомой непрерывности, или аксиомой отделимости.
УПРАЖНЕНИЕ 1. Докажите следующие утверждения:
1.В множестве действительных чисел имеется только один нуль.
2.В множестве действительных чисел у каждого элемента имеется единственный противоположный элемент.
3.В множестве действительных чисел имеется только одна единица.
4.В множестве действительных чисел для каждого x = 0
имеется только один обратный элемент x−1.
Как известно из курса средней школы, множество вещественных чисел R можно отождествить с множеством точек на прямой. Поэтому часто мы будем называть элементы множества R точками, а также прибегать к другой геометрической терминологии.
Если a и b произвольные действительные числа и a < b, то множество
{x R : a < x < b}
называется интервалом (или открытым промежутком) и обозначается символом (a, b). Множество
{x R : a ≤ x ≤ b}
называется отрезком (или замкнутым промежутком) и обозначается [a, b]. Рассматриваются также и полуоткрытые промежутки (полуинтервалы):
[a, b) = {x R : a ≤ x < b};
(a, b] = {x R : a < x ≤ b}.
Всевозможные промежутки (открытые, замкнутые, полуоткрытые) будем обозначать символом a, b . Длиной промежутка a, b называется число, равное b − a.
20 Глава 1. Предел последовательности
ОПРЕДЕЛЕНИЕ 2.1. Пусть A из R (A R) – произвольное множество. Элемент a A называется максимальным или наибольшим (минимальным или наименьшим) элементом в множестве A, если для любого a A выполнено
a |
≤ |
a (a |
≥ |
a ) |
a = max a |
} |
(a = min a |
) |
|
|
. Запись: |
a A { |
a A { |
} . |
ЗАМЕЧАНИЕ. Таким образом,
a = max{a}
a A
тогда и только тогда, когда максимальный элемент a A и для всех элементов a A выполнено a ≤ a .
ПРИМЕР 1. Множество [a, b) = {x R : a ≤ x < b} имеет минимальный элемент, равный a, но не имеет максимального элемента. 

ОПРЕДЕЛЕНИЕ 2.2. Число |a| = max{a, −a} называется абсолютной величиной (модулем) числа a.
УПРАЖНЕНИЕ 2. Пользуясь аксиомой порядка, доказать, что если в числовом множестве A имеется максимальный (минимальный) элемент, то этот элемент единственный (методом от противного).
УПРАЖНЕНИЕ 3. Доказать следующие свойства абсолютной величины:
a.a R : |a| ≥ 0 и |a| = 0 тогда и только тогда, когда a = 0.
b.|ab| = |a| |b|.
c.|a + b| ≤ |a| + |b| (неравенство треугольника).
d.||a| − |b|| ≤ |a − b|.
e.Пусть ε > 0 – произвольное число. Тогда для любого x R следующие высказывания эквивалентны:
|x| < ε и −ε < x < ε.
ОПРЕДЕЛЕНИЕ 2.3. Говорят, что множество A R ограничено сверху (снизу), если существует число M R такое, что для любого a A выполнено a ≤ M (a ≥ M). Число M называется в этом случае верхней (нижней) гранью множества A.
ПРИМЕР 2. Рассмотрим множество A = [0; 1). Всякое число M ≥ 1 является верхней гранью этого множества, а всякое число M ≤ 0 является нижней гранью множества A. 

