
Лосев-КлячинМиклюков МА в КИ
.pdf
§1. Понятие функции |
51 |
Область определения сложной функции, вообще говоря,
может измениться по сравнению с X.
ln(x + 1) есть суперпозиция
√
трех функций z = x + 1, t = ln(z) и y = t. 

УПРАЖНЕНИЕ 3. Привести пример, в котором область определения суперпозиции сужается по сравнению с первоначальной.
УПРАЖНЕНИЕ 4. Привести пример, в котором область определения суперпозиции – пустое множество.
Пусть даны две функции y = f(x) и x = g(y). Предположим, что областью определения f и областью значений g является одно и то же непустое множество. Если f(g(y)) = y для всех y из области определения g, то функцию x = g(y)
называют обратной к функции y = f(x) и обозначают x = f−1(y).
√
ПРИМЕР 5. Функция x = 3 y является обратной к функции y = x3. 
ПРИМЕР 6. Обратной функцией к функции y = x2 является√многозначная (вообще говоря, двузначная) функция x = ± y, график которой состоит из двух "ветвей". 

Различают несколько способов задания функции:
Аналитический способ, т.е. задание функции с помощью одной или нескольких аналитических формул.
ПРИМЕР 7. y = ln(1 − x2).  ПРИМЕР 8. Функция
ПРИМЕР 8. Функция
y = D(x) = |
1, |
если |
x |
рациональное |
0, |
если |
x −− |
иррациональное |
носит название функции Дирихле1. 
ПРИМЕР 9. Функция y = [x] (целая часть числа x) определяется следующим образом: если x = n + r, где n – целое число и 0 ≤ r < 1, то [x] = n.
Графический способ, когда задается график функции.
Параметрический способ. Иногда график может быть задан в виде системы функций
x = x(t) и y = y(t) , где параметр t a, b .
1Дирихле Петер Густав Лежен (13.2.1805-5.5.1859). Род. в Дюрене (Германия). Автор ряда значительных результатов в теории чисел, математическом анализе, механике, математической физике.
52 |
Глава 2. Предел функции |
При изменении параметра t на a, b точка (x(t), y(t)) описывает некоторую дугу γ в плоскости (x, y). Обозначим через X ортогональную проекцию γ на ось x-ов. Тогда над каждой точкой x X расположены одна или несколько точек на дуге γ. Тем самым, каждому x X по определенному правилу ставится в соответствие одно или несколько значений y, т.е. задана некоторая (вообще говоря, многозначная) функция y = y(x), графиком которой является дуга γ.
В этом случае говорят, что функция y = y(x) задана параметрически.
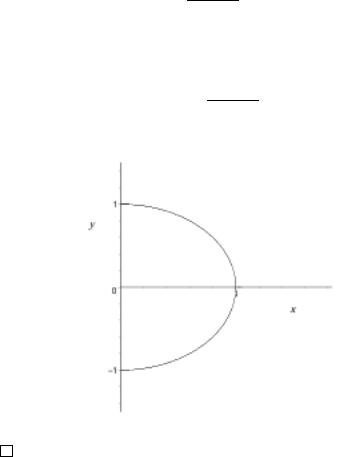
ПРИМЕР 10. Нетрудно видеть, что параметрически заданная функция
x = cos t, y = sin t, −π ≤ t ≤ π,
описывает дугу окружности
y = ± 1 − x2, 0 ≤ x ≤ 1.
Действительно, мы имеем
x2 + y2 = cos2 t + sin2 t = 1.
√
Следовательно, y = ± 1 − x2. Поскольку x = cos t и t [−π, π], то 0 ≤ x ≤ 1.
Табличный способ, при котором выписываются в виде таблицы значения аргумента и соответствующие им значения функции.
Различают явный и неявный способы задания функции. Аналитический и табличный – способы явного задания.

§2. Некоторые функции одной переменной |
53 |
Опишем неявный способ. Предположим, что значения двух переменных величин x и y связаны между собой некоторым соотношением
F (x, y) = 0. |
(1) |
Если функция y = f(x), определенная на множестве X, такова, что уравнение (1) при подстановке в него вместо y выражения f(x) обращается в тождество относительно x, т.е. F (x, f(x)) ≡ 0, то говорят, что функция y = f(x) есть неявная функция, определ¨енная уравнением (1).
ПРИМЕР 11. Многозначная функция y = ±√x может быть
задана также неявно посредством уравнения x − y2 = 0. Т.е. одна и та же функция может задаваться как явно, так и неявно. 

ПРИМЕР 12. Рассмотрим неявную функцию y = f(x), определяемую соотношением
cos x lnx − cos y − lny = 0
(берем x и находим y = f(x)). Можно доказать (попробуйте!), что эта функция в явном виде с помощью известных нам формул не выражается. 

§2. Некоторые функции одной переменной
1) Обратные тригонометрические функции
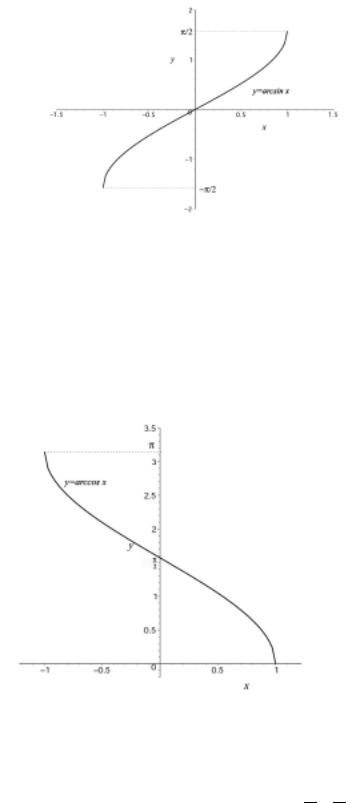
а) Функция y = arcsin x. Рассмотрим функцию y = sin x. Ее областью определения является вся числовая прямая R, а областью значений отрезок [−1, 1]. Всякая прямая y = C, где C [−1, 1], пересекает график функции в бесконечном количестве точек, т.е. обратная функция, которую обозначают x = Arcsin y, является бесконечнозначной. Обычно рассматривают лишь одну “ветвь” этой функции, отвечающую изменению x между −π2 и π2 . Каждому y [−1, 1] соответ-
ствует ровно одно x [−π2 , π2 ]. Его обозначают x = arcsin y
и называют главным значением (главной “ветвью") функции x = Arcsin y. Ясно, что
Arcsin y = (−1)k arcsin y + kπ (k = 0, ±1, ±2, . . .) .
54 |
Глава 2. Предел функции |
б) Функция y = arccos x. Рассуждая, как и выше с функцией y = cos x, получаем многозначную обратную функцию x = Arccos y, y [−1, 1]. Ее главная "ветвь"
x = arccos y, y [−1, 1], x [0, π].
При этом
Arccos y = 2kπ ± arccos y (k = 0, ±1, ±2, . . .) .
в) Функция y = arctg x. Обратная к функции y = tg x функция x = Arctg y является бесконечнозначной. Ее главная “ветвь”
x = arctg y, y (−∞, ∞), x (−π2 , π2 ).
Тогда справедливо соотношение
Arctg y = kπ + arctg y (k = 0, ±1, ±2, . . .).

§2. Некоторые функции одной переменной |
55 |
г). Функция y = arcctg x. Обратная к y = ctg x функция x = Arcctg y является бесконечнозначной. Главная “ветвь"
x = arcctg y, x (0, π), y (−∞, ∞).
Справедливо соотношение
Arcctg y = kπ + arcctg y (k = 0, ±1, ±2, . . .).
Установим соотношение между функциями y = arcsinx и y = arctg x:
arctg x = arcsin |
√ |
x |
x R, |
|||
|
|
|||||
1 + x2 |
||||||
arcsin x = arctg |
√ |
|
x |
x (−1, 1). |
||
|
|
|||||
1 − x2 |
|
|||||
56 |
Глава 2. Предел функции |
Докажем первое из соотношений. Положим α = arctg x, тогда tg α = x. Получаем:
sin α = |
|
tg α |
|
|
|
. |
|
± |
|
||
1 + tg2 α |
|||
Так как на интервале (−π2 , π2 ) знаки синуса и тангенса одного и того же угла (аргумента) совпадают, то
sin α = |
|
tg α |
|
√ |
x |
|
|
|
= |
|
. |
||
|
|
|||||
1 + tg2 α |
1 + x2 |
|||||
Знак меняется, если меняется промежуток. Отсюда
arctg x = α = arcsin√ x . 1 + x2
УПРАЖНЕНИЕ 1. Проверить второе соотношение самостоятельно.
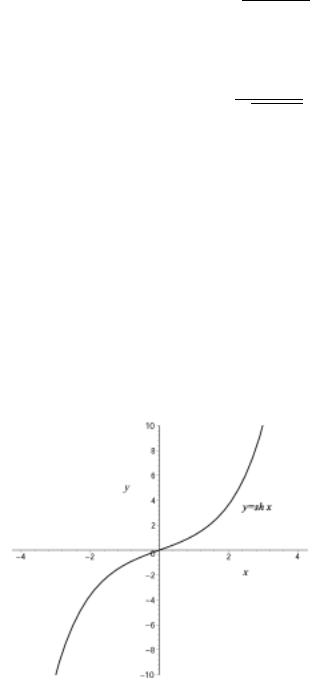
2) Гиперболические функции.
По определению полагаем для любых x R
shx = |
1 |
(ex − e−x), |
chx = |
1 |
(ex + e−x). |
|
|
||||
2 |
2 |
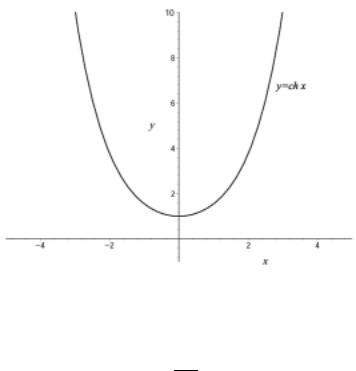
Данные функции имеют областью определения всю числовую прямую. При этом sh x функция нечетная, а ch x функция четная.
§3. Точные грани, максимум и минимум функции |
57 |
УПРАЖНЕНИЕ 2. Доказать формулу ch2 x − sh2 x = 1.
УПРАЖНЕНИЕ 3. Построить эскизы графиков y = th x = chsh xx, y = cth x = chsh xx.
УПРАЖНЕНИЕ 4. Доказать, что
sh(x + y) = shx chy + chx shy, ch(x + y) = chx chy + shx shy.
§3. Точные грани, максимум и минимум функции
Пусть y = f(x) – функция, определенная на множестве X R с областью значений Y R.
ОПРЕДЕЛЕНИЕ 3.1. Функция y = f(x) называется ограниченной сверху (снизу), если множество Y ограничено сверху (снизу), т.е. существует постоянная M такая, что
f(x) ≤ M x X (f(x) ≥ M x X).
Число M называется верхней (нижней) гранью функции f(x) на множестве X.
Функция называется ограниченной, если она ограничена и сверху и снизу, т. е. найдется постоянная M такая, что
|f(x)| ≤ M x X, .
Наименьшая (наибольшая) из всех верхних (нижних) граней называется точной верхней (точной нижней) гранью функции f(x) на множестве X и обозначается
sup f(x) ( inf f(x)).
x X x X
58 |
Глава 2. Предел функции |
Ясно, что A = supx X f(x) тогда и только тогда, когда выполняются условия:
1)f(x) ≤ A x X ;
2)A < A найдется x X : f(x) > A (т.е. A – наименьшая из всех верхних граней).
Аналогично, можно записать, что A = infx X f(x) тогда и только тогда, когда выполняются условия:
1) f(x) ≥ A x X (т.е. A – верхняя грань f); 2) A > A найдется x X : f(x) < A .
ОПРЕДЕЛЕНИЕ 3.2. Число A называется максимумом (минимумом) функции y = f(x) на множестве X, если оно является максимальным (минимальным) элементом множества Y , т.е.
1)f(x) ≤ A (≥ A) x X ;
2)найдется x X : f(x) = A (т.е. эта верхняя грань достигается в некоторой точке).
Максимум (минимум) функции обозначается
A = max f(x), |
(A = min f(x)). |
x X |
x X |
В общем случае, функция может иметь точную верхнюю (нижнюю) грань, но не иметь максимума (минимума) (построить примеры!).
Если функция не ограничена сверху (снизу), то часто говорят, что она имеет бесконечную точную верхнюю (нижнюю) грань и пишут
sup f(x) = +∞ ( inf f(x) = −∞).
x X |
x X |
|
|
§4. Пределы функции по Коши и по Гейне
Пусть E R – множество и a – точка сгущения E (которая может как принадлежать E, так и не принадлежать). Пусть y = f(x) – функция, определенная на множестве E.
ОПРЕДЕЛЕНИЕ 4.1. (Предел функции по Коши). Говорят, что число A является пределом функции y = f(x) при x → a и пишут
lim f(x) = A,
x→a
если
ε > 0 δ(ε) > 0 : x E, x = a, |x − a| < δ(ε)
выполнено
|f(x) − A| < ε.

§4. Пределы функции по Коши и по Гейне |
59 |
Множество {x R : |x − a| < δ, x = a} называется проколотой δ - окрестностью точки a.
Теперь определение предела функции в точке можно переформулировать следующим образом.
Число A называется пределом функции y = f(x) в точке a (при x → a), если для любой ε-окрестности точки A найдётся такая δ(ε)-окрестность точки a, что при изменении x в проколотой δ(ε)-окрестности точки a значения функции меняются в ε-окрестности точки A (см. рисунок ниже).
y
|
|
y = f(x) |
||||||||||||
A + ε |
|
|
|
|
|
|
|
|
|
|
||||
A |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||||
A − ε |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|||||||||||
|
||||||||||||||
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
a − |
δ(ε) |
a a + δ(ε) |
||||||||||||
ПРИМЕР 1. Докажем, что lim x2 = 0.
x→0
Зададим произвольно ε > 0 и будем искать δ(ε) > 0 такое, что
x R, x = 0, |x| < δ(ε)
2 |
|
| |
x2 |
| |
< ε. Решаем неравенство |
| |
| |
< ε, или |
|||
выполнено |
|
|
x2 |
|
|||||||
|x| |
< ε. Т.е. |x| < √ |
|
и можно положить δ(ε) = |
√ |
|
. |
|||||
ε |
ε |
||||||||||
ЗАМЕЧАНИЕ. Число A не является пределом f(x) при x → a, x E, если ε > 0 такое, что δ > 0 найдется x E, x = a, |x − a| < δ, однако |f(x) − A| ≥ ε.
ОПРЕДЕЛЕНИЕ 4.2. (Предел функции по Гейне2). Число A называется пределом функции y = f(x) при x → a, x E, если для любой последовательности {xn}, xn E, xn = a, xn → a выполнено f(xn) → A при n → ∞.
ТЕОРЕМА 4.1. Определения предела функции в точке в смысле Коши и в смысле Гейне эквивалентны.
2Гейне Генрих Эдуард (16.3.1821-21.10.1881). Род. в Берлине (Германия). Основные труды относятся к математической физике, теории уравнений в частных производных.

60 |
Глава 2. Предел функции |
Доказательство. Пусть A есть предел функции y = f(x) при x → a в смысле Коши. Покажем, что функция имеет тот же самый предел A и в смысле Гейне. Зададим произвольно последовательность {xn} со свойствами: xn E, xn = a,
xn → a. Покажем, что f(xn) → A при n → ∞. Пусть ε > 0 – произвольно. Найдем δ(ε) > 0 из первого определения такое, что
x = a, |x−a| < δ(ε) |
выполнено |f(x)−A| < ε. (1) |
Далее заметим, что |
N = N(δ(ε)), такое что n > N |
выполнено |xn − a| < δ(ε). Тогда из (1) вытекает
n > N(δ(ε)) : |f(xn) − A| < ε.
Таким образом, A – предел функции y = f(x) по Гейне.
Пусть A есть предел функции y = f(x) в смысле Гейне. Требуется доказать, что ε > 0 δ(ε) > 0 такое, что
x E, x = a, |x − a| < δ(ε) выполнено |f(x) − A| < ε. Предположим противное, т.е.
ε > 0 : δ > 0 найдётся x E, x = a, |x − a| < δ
и такой, что
|f(x) − A| ≥ ε. |
|
|
|
|
|
|
||
Пусть |
1 |
|
|
|
|
1 |
|
|
δ1 = 1, δ2 = |
, . . . , δn |
= |
|
. . . . |
||||
|
|
|||||||
2 |
n |
|||||||
По каждому δn находится |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
xn E такое, что xn = a, |xn −a| < |
|
, |
и |
|f(xn)−A| ≥ ε. |
||||
n |
||||||||
Получаем противоречие с предположением, поскольку возникла последовательность {xn} → a, для которой f(xn) →A.
§5. Первый "замечательный" предел
ТЕОРЕМА 5.1. Существует предел
lim sin x = 1 .
x→0 x
Доказательство. Покажем, что x (0, π2 ) выполнено
sin x < x < tg x. |
(1) |
