
Шведенко Начала анализа функций комплексной переменной 2008
.pdffederalxnoe AgEntstwo po obrazowani` moskowskij invenerno{ fizi~eskij institut
(gosudarstwennyj uniwersitet)
s. w. {WEDENKO
na~ala analiza funkcij
kompleksnoj peremennoj
rEKOMENDOWANO umo \qDERNYE FIZIKA I TEHNOLOGII" W KA^ESTWE U^EBNOGO POSOBIQ DLQ STUDENTOW
WYS[IH U^EBNYH ZAWEDENIJ
mOSKWA 2008
udk 517.53 (075) bbk 22.161.5Q7
{34
{W E D E N K O s. w. nA^ALA ANALIZA FUNKCIJ KOMPLEKSNOJ PEREMENNOJ: m.: mifi, 2008. | 356 c.
dANO SISTEMATI^ESKOE IZLOVENIE TOJ ^ASTI WUZOWSKOGO KURSA MATEMATI^ESKOGO ANALIZA, KOTORU@ W U^EBNYH PRO-
GRAMMAH OBY^NO NAZYWA@T TEORIEJ FUNKCIJ KOMPLEKSNOJ PEREMENNOJ. tEKST SOPROWOVDAETSQ MNOGO^ISLENNYMI RISUN- KAMI, WKL@^AET ZADA^I, UPRAVNENIQ, RAZBOR BOLX[OGO ^ISLA PRIMEROW.
aDRESOWAN STUDENTAM, IZU^A@]IM DANNYJ PREDMET KAK PO OBY^NOJ, TAK I UGLUBLENNOJ PROGRAMME.
rECENZENT: KAND. FIZ.-MAT NAUK, DOCENT d.s.tELQKOWSKIJ
iZDANIE PODGOTOWLENO W RAMKAH iNNOWACIONNOJ OB]EOB- RAZOWATELXNOJ PROGRAMMY.
ISBN 978-5-7262-1023-0 |
c mOSKOWSKIJ |
|
|
|
INVENERNO-FIZI^ESKIJ INSTITUT |
(GOSUDARSTWENNYJ UNIWERSITET), 2008
rEDAKTOR n. n. aNTONOWA |
|
|
pODPISANO W PE^ATX |
fORMAT 60 84 1/16 |
|
pE^. L. 22,25 u^.-IZD. L. 22,5 |
iZD. N 1/33 tIRAV |
150 \KZ. |
mOSKOWSKIJ INVENERNO-FIZI^ESKIJ INSTITUT (GOSUDARSTWENNYJ UNIWERSITET).
115409, mOSKWA, kA[IRSKOE [., 31 tIPOGRAFIQ \tROWANT" G. tROICK mOSKOWSKOJ OBL.

3
pREDISLOWIE
dANNAQ KNIGA NAPISANA NA OSNOWE LEKCIJ PO KURSU \tEORIQ FUNKCIJ KOMPLEKSNOJ PEREMENNOJ", MNOGOKRATNO ^ITAW[IHSQ AW- TOROM W mOSKOWSKOM INVENERNO-FIZI^ESKOM INSTITUTE, W SO^ETA- NII S OPYTOM PROWEDENIQ IM PRAKTI^ESKIH ZANQTIJ PO DANNOMU RAZDELU MATEMATI^ESKOGO ANALIZA.
pRI NAPISANII KNIGI AWTOR STAWIL PERED SOBOJ SLEDU@]IE OGRANI^ENIQ.
1.oBRA]AQSX (^TO NEIZBEVNO) K PONQTIQM I FAKTAM IZ PRED- [ESTWU@]EGO KURSA DEJSTWITELXNOGO ANALIZA, IZBEGATX SSYLOK NA TE EGO RAZDELY, K TRADICIONNOMU IZLOVENI@ KOTORYH MOVNO
WYSKAZATX PRETENZII. w ^ASTNOSTI, \TO OTNOSITSQ K RAZDELAM \kRIWOLINEJNYE INTEGRALY"1 I \nESOBSTWENNYE INTEGRALY S PARAMETROM"2.
2.wYDERVATX ROWNYJ UROWENX IZLOVENIQ, NE PRIBEGAQ K STAW[EMU PRIWY^NYM W MATEMATI^ESKIH KURSAH PRIEMU \WYBO- RO^NOJ STROGOSTI".
3.oTDAWAQ DOLVNOE ROLI RISUNKOW3 W POQSNENII RASSUV- DENIJ, OTKAZATXSQ OT ^REZMERNO RASPROSTRANIW[EGOSQ (OSOBENNO PRI OPISANII DEJSTWIJ NA KOMPLEKSNOJ PLOSKOSTI) PRIEMA \RI- SUNO^NOJ ARGUMENTACII", KOGDA RISUNKI SLUVAT NE STOLXKO IL- L@STRACIEJ LOGI^ESKIH DOWODOW, SKOLXKO SPOSOBOM \UPROSTITX" DOKAZATELXSTWA NEZAMETNOJ PODMENOJ (POSREDSTWOM \UDA^NOGO" RISUNKA) \NEUDOBNOGO" OB]EGO SLU^AQ BOLEE \UDOBNYM" ^AST-
NYM.
1 kAVDYJ SLU[ATELX LEKCIJ PO ANALIZU WSPOMNIT TOROPLIWOSTX, S KOTOROJ WWODILISX PONQTIQ KONTURA I INTEGRALA PO KONTURU, A KAV- DYJ SOWESTLIWYJ LEKTOR | ^UWSTWO NELOWKOSTI, ISPYTYWAEMOE IM PRI
\WYWODE" FORMULY gRINA.
2 tRADICIONNYE TEOREMY \TOGO RAZDELA IME@T BOLEE VESTKIE USLO- WIQ PO SRAWNENI@ S TEMI, KOTORYE PREDOSTAWLQ@T PRILOVENIQ (NAPRI-
MER, W RAMKAH PREOBRAZOWANIQ lAPLASA).
3 w \TOJ KNIGE IH 133 STOIT OTMETITX, ^TO W IZLOVENIQH KLASSIKOW RISUNKI LIBO OTSUTSTWU@T (NAPRIMER, U kO[I), LIBO KRAJNE REDKI.

4
4.oTKAZATXSQ OT SLOW I SLOWOSO^ETANIJ \O^EWIDNO", \LEG- KO WIDETX", \NETRUDNO POKAZATX\, KOTORYE W MATEMATIKE DAWNO UTRATILI IZNA^ALXNYJ SMYSL I PREWRATILISX W UKAZATELI SLA- BYH MEST I PROBELOW W RASSUVDENIQH.
5.uSTANOWITX PO PERWOISTO^NIKAM PROISHOVDENIE OSNOW-
NYH PONQTIJ I FAKTOW TEORII FUNKCIJ KOMPLEKSNOJ PEREMENNOJ, DAW TO^NYE SSYLKI.1
sTRUKTURNO KNIGA SOSTOIT IZ 20 GLAWOK (ILI SEKCIJ), NAZWA- NIQ KOTORYH MOGUT ZWU^ATX KAK WOPROSY, NA KOTORYE AWTOR STRE- MILSQ DATX PO WOZMOVNOSTI POLNYE (W RAMKAH ZADANNOGO OB_EMA KNIGI I \RUDICII AWTORA), NO NEPREMENNO WNQTNYE I ARGUMENTI- ROWANNYE OTWETY. sREDI WYWODIMYH UTWERVDENIJ, W KOTORYH KONCENTRIRU@TSQ \TI OTWETY, LI[X NAIBOLEE FUNDAMENTALXNYE I IMENNYE SNABVENY TITULOM (\TEOREMA", \LEMMA", \KRITERIJ" I T. P.), UTWERVDENIQ VE \WTOROGO RQDA", NE TREBU@]IE ^ASTOGO K NIM OBRA]ENIQ, WYDELQ@TSQ W TEKSTE DWOJNOJ WERTIKALXNOJ ^ERTOJ.
iSPOLXZOWANIEM DWUHUROWNEWOGO [RIFTA MATERIAL RAZDELQ- ETSQ NA OSNOWNOJ (PRIMERNO SOOTWETSTWU@]IJ PROGRAMME KURSA, PRINQTOJ W mifi) I DOPOLNITELXNYJ, W KOTORYJ WYNESENY WY- HODQ]IE ZA RAMKI KURSA (NO PRIMYKA@]IE K NEMU) UTWERVDENIQ, OTDELXNYE DOKAZATELXSTWA (ILI IH FRAGMENTY), ISTORI^ESKIJ KOMMENTARIJ I WSQ^ESKIE PODROBNOSTI.
zADA^I, RAZBIRAEMYE W KA^ESTWE PRIMEROW, WZQTY IZ POPULQR- NYH ZADA^NIKOW, ZADA^I VE UPRAVNENIJ (PREDLAGAEMYE W KONCE KAVDOJ GLAWKI) W BOLX[INSTWE SOSTAWLENY AWTOROM.
|LEKTRONNYJ ADRES AWTORA | sershvedenko@mail.ru
1 lXWINAQ IH DOLQ PRIHODITSQ NA RABOTY kO[I, SOSTAWIW[IE OS- NOWU \TOJ TEORII, NO, K SOVALENI@, NE OFORMLENNYE IM W WIDE SISTE- MATI^ESKI IZLOVENNOGO KURSA (PODOBNOGO EGO \kURSU ANALIZA" [26]), A OSTAWLENNYE W WIDE OTDELXNYH STATEJ, MEMUAROW I T. P., RAZO[ED[IHSQ PO MNOGO^ISLENNYM TOMAM EGO pOLNOGO SOBRANIQ SO^INENIJ [28].
5
I. ~TO NAZYWA@T KOMPLEKSNOJ
PLOSKOSTX@ I W ^EM EE OTLI^IE OT
DEJSTWITELXNOJ
KOMPLEKSNAQ PLOSKOSTX C | \TO TO, ^EM STANOWITSQ DEJST- WITELXNAQ KOORDINATNAQ PLOSKOSTX R2 (S ee TRADICIONNYMI OSQMI x (ABSCISS) I y (ORDINAT) I \LEMENTAMI, MYSLIMYMI I KAK TO^KI, I KAK WEKTORY1) PRI WWEDENII W NEJ (W DOPOLNENIE K UVE IME@]IMSQ OPERACIQM SLOVENIQ WEKTOROW I UMNOVENIQ IH NA DEJSTWITELXNYE ^ISLA) OPERACII UMNOVENIQ WEKTORA NA
WEKTOR PO PRAWILU:
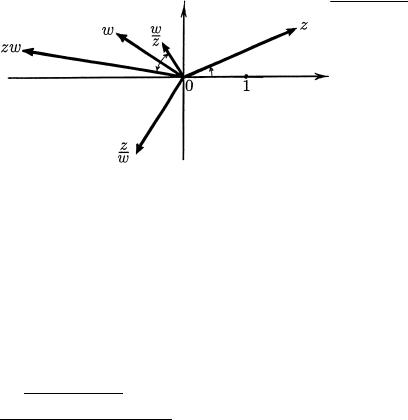
PROIZWEDENIE NENULEWOGO WEKTORA z NA NENULEWOJ WEKTOR w
ESTX OBOZNA^AEMYJ z w WEKTOR (\TOJ VE PLOSKOSTI), DLINA KOTO- ROGO RAWNA PROIZWEDENI@ DLIN PEREMNOVAEMYH WEKTOROW ;jzwj= jzjjwj , A UGOL, KOTORYJ ON SOSTAWLQET S OSX@ ABSCISS, RAWEN SUM-
ME UGLOW MEVDU \TOJ OSX@ I SOMNOVITELQMI (PRI OBY^NOM SO-
GLA[ENII S^ITATX POLOVITELXNYM OTS^ET UGLOW \PROTIW HODA ^ASOWOJ STRELKI" RIS. 1)
rIS. 1
PROIZWEDENIEM z w WEKTOROW z I w, SREDI KOTORYH ESTX NU-
LEWOJ, S^ITAETSQ NULEWOJ WEKTOR.
1 oTKLADYWAEMYE OT L@BOJ TO^KI.

6
oT TRADICIONNYH SKALQRNOGO I WEKTORNOGO UMNOVENIJ WWODIMU@ OPERACI@ OTLI^AET TO, ^TO EE REZULXTAT ESTX WEKTOR, PRI^EM TOJ VE PLOSKoSTI, KAKOJ PRINADLEVAT SOMNOVITELI.
wOT PRQMYE SLEDSTWIQ DANNOGO PRAWILA PEREMNOVENIQ WEKTOROW.
1.sOBL@DA@TSQ PRIWY^NYE \ZAKONY": z w = wz | PEREMESTITELXNYJ,
(z w) = z(w ) | SO^ETATELXNYJ,
(z+w) = z +w | RASPREDELITELXNYJ.
2.BYPOLNIMA OBRATNAQ K UMNOVENI@ OPERACIQ DELENIQ L@BOGO WEKTORA NA L@BOJ NENULEWOJ WEKTOR (KAK NA RIS. 1).
nA QZYKE ALGEBRY \TO OZNA^AET, ^TO PLOSKOSTX C QWLQETSQ POLEM, W TO WREMQ KAK PLOSKOSTX R2 ESTX LI[X LINEJNOE PROSTRANSTWO (NAD
POLEM R DEJSTWITELXNYH ^ISEL).
nA WOPROS, MOVNO LI PREWRATITX W POLE KOORDINATNOE PROSTRANST-
OTWET DAET TEOREMA fROBENIUSA1: WWESTI W PRO- STRANSTWE Rn n > 1, OPERACI@ yMNOVENIQ WEKTORA NA WEKTOR c WY-
POLNENIEM PEREMESTITELXNOGO, SO^ETATELXNOGO I RASPREDELITELXNOGO ZAKONOW I WOZMOVNOSTX@ DELENIQ NA NENULEWYE WEKTORY MOVNO LI[X PRI n=2 (I IMENNO UKAZANNYM WY[E SPOSOBOM).
3. dLQ L@BOGO NENULEWOGO WEKTORA z 2 C |
|
I n = 2 3 : : : |
||||||||||||
OPREDELENY n ZNA^ENIJ |
KORNQ n-J STEPENI IZ |
|
z |
, OBOZNA- |
||||||||||
^AEMYE (WSE WMESTE I KAVDYJ W OTDELXNOSTI) p |
|
. BSE ONI |
||||||||||||
z |
||||||||||||||
|
|
|
p2 |
|
|
|
n |
|
|
|
|
|||
|
|
|
pj j |
|
|
|
|
|
||||||
QWLQ@TSQ WEKTORAMI DLINY n |
jzj |
(ZDESX n |
|
jzj |
| ARIFME- |
|||||||||
TI^ESKIJ KORENX IZ POLOVITELXNOGO ^ISLA |
|
z ), |
|
|
OBRAZU@T |
|||||||||
DRUG S DRUGOM UGLY, KRATNYE |
|
|
, PRI^EM ODIN IZ WEKTO- |
|||||||||||
n |
||||||||||||||
|
|
|
|
|
n RAZ MENX[IJ |
|||||||||
ROW pz SOSTAWLQET S OSX@ ABSCISS UGOL, W |
||||||||||||||
n |
|
|
|
|
|
|
|
|
|
|
||||
UGLA MEVDU \TOJ OSX@ I WEKTOROM z. kAK SLEDSTWIE, KON-
CEWYE TO^KI WEKTOROW pn z, OTLOVENNYH OT OB]EGO NA^ALA,
1 fROBENIUS (Frobenius, Georg Ferdinand, 1849 {1917) | NEMECKIJ MATEMATIK. pOLNU@ FORMULIROWKU I DOKAZATELXSTWO USTANOWLENNOJ
IM (W 1877 G.) TEOREMY MOVNO NAJTI, NAPRIMER, U l. q. oKUNEWA [14].
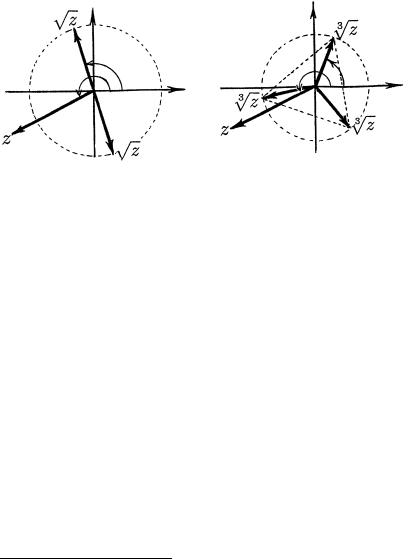
7
OBRAZU@T WER[INY PRAWILXNOGO n-UGOLXNIKA, WPISANNOGO W
OKRUVNOSTX RADIUSA pn jzj (NA RIS. 2 IZOBRAVENY WEKTORY z pz I p3 z PRI jzj > 1). dLQ NULEWOGO WEKTORA z EDINSTWENNYM ZNA^ENIEM pn z QWLQETSQ NULEWOJ WEKTOR.
rIS. 2
4.BEKTORY, KOLLINEARNYE OSI ABSCISS, WEDUT SEBQ PRI
SLOVENII, WY^ITANII, UMNOVENII I DELENII KAK DEJSTWITELXNYE ^ISLA I POTOMU NA KOMPLEKSNOJ PLOSKOSTI MOGUT IMETX OB]IE S NIMI OBOZNA^ENIQ. w ^ASTNOSTI, NULEWOJ WEK- TOR I EDINI^NYJ NAPRAWLQ@]IJ WEKTOR OSI ABSCISS ZAPISY-
WA@TSQ KAK 0 I 1.
5.kWADRATY (REZULXTATY UMNOVENIJ NA SEBQ) NENULEWYH WEKTOROW, KOLLINEARNYH OSI ORDINAT, OKAZYWA@TSQ WEKTORAMI, KOLLINEARNYMI OSI ABSCISS, NO PROTIWOPOLOVNYMI
EJ PO NAPRAWLENI@. w ^ASTNOSTI, EDINI^NYJ NAPRAWLQ@]IJ WEKTOR OSI ORDINAT, KOTORYJ NA KOMPLEKSNOJ1PLOSKOSTI OBO-
1 w OTLI^IE OT DEJSTWITELXNOJ.
8
ZNA^A@T1 i, OBLADAET SWOJSTWOM i2 = ;1. nENULEWYE WEKTO- RY, KOLLINEARNYE OSI ORDINAT, IME@T PO\TOMU PREDSTAWLE-
NIE iy (S NENULEWYM y 2R ) I WYPOLNQ@T ROLX KWADRATNYH KORNEJ IZ OTRICATELXNYH DEJSTWITELXNYH ^ISEL.
rIS. 3
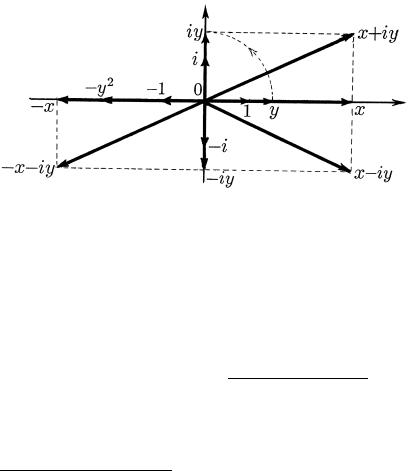
|TI OBOZNA^ENIQ POZWOLQ@T ZAPISYWATX WEKTORY z 2 C
W WIDE z = x+iy, GDE x I y | DEJSTWITELXNYE ^ISLA, KO-
TORYE ODNOWREMENNO MOVNO RASSMATRIWATX I KAK WEKTORY PLOSKOSTI C , KOLLINEARNYE OSI ABSCISS WEKTOR iy OBRETA- ET PRI \TOM SMYSL PROIZWEDENIQ WEKTOROW i I y (RIS. 3).
wEKTORY z w : : : |
2 |
C , |
2 |
|
ZAPISANNYE W WIDE SO^ETANIJ |
z = x+iy w =u+iv : : : , I ESTX KOMPLEKSNYe ^ISLA , PRAWI- LA SLOVENIQ, WY^ITANIQ, UMNOVENIQ I DELENIQ KOTORYH |
S REZULXTATAMI W WIDE TAKIH VE SO^ETANIJ | OPREDELQ@T- SQ PRAWILAMI WEKTORNOGO SLOVENIQ I WWEDENNOJ OPERACII
WEKTORNOGO UMNOVENIQ
1 iSKL@^AQ \LEKTROTEHNIKOW, OBOZNA^A@]IH EGO j , POSKOLXKU i ONI PRIWYKLI WOSPRINIMATX KAK WELI^INU TOKA.
2 lAT. complexio | SO^ETANIE.
9
(x+iy) (u+iv) = (x u)+i(y v) (x+iy)(u+iv) = x(u+iv)+iy(u+iv) =
|
|
= xu+xiv+iyu+iyiv = (xu;yv)+i(xv+yu) |
||
x+iy |
= |
(x+iy)(u;iv) |
= xu2+iyu;xiv;i22yv2 = |
|
u+iv |
|
(u+iv)(u;iv) |
u +ivu;uiv;i v |
|
|
|
= xu+yv + i yu;xv |
(PRI USLOWII u+iv =0). |
|
|
|
u2+v2 |
u2+v2 |
6 |
wOSPRINIMAQ KOMPLEKSNYE ^ISLA z =x+iy KAK WEKTORY
PLOSKOSTI1 C IH, SLEDUQ gAUSSU2, ODNOWREMENNO PREDSTAW- LQ@T SEBE I KAK TO^KI3 \TOJ PLOSKOSTI | KONCEWYE TO^KI
WEKTOROW, OTKLADYWAEMYH OT NA^ALA KOORDINAT.
rIS. 4
iRLANDSKIJ MATEMATIK gAMILXTON4, W MONOGRAFII KOTOROGO [35] OKON^ATELXNO OFORMILOSX PONQTIE WEKTORA5, PREDLOVIL WOSPRINIMATX
KOMPLEKSNYE ^ISLA KAK (UPORQDO^ENNYE) PARY DEJSTWITELXNYH ^ISEL:
1 s^ITAQ, ^TO KAVDYJ IZ NIH MOVNO OTLOVITX OT L@BOJ EE TO^KI.
2 gAUSS (Gauss, Carl Friedrich, 1777{1855) | NEMECKIJ MATEMATIK. nA RIS. 4 | ZAIMSTWOWANNYJ IZ [33] (Bd. VIII, S. 105) FRAGMENT EGO ZA- METOK 1805 G. | ODNO IZ PERWYH IZOBRAVENIJ KOMPLEKSNOJ PLOSKOSTI.
3 iNOGDA NAZYWAQ KOMPLEKSNOE ^ISLO x+iy AFFIKSOM IZOBRAVA@-
]EJ EGO TO^KI (LAT. a xus | PRIKREPLENNYJ).
4 Hamilton, William Rowan, 1805 {1865.
5 sOEDINIW[EGO PONQTIQ DLINY I NAPRAWLENIQ I OPREDELQEMOGO gA- MILXTONOM | W OTLI^IE OT RADIUSA{WEKTORA, WYRAVA@]EGO LI[X DLI-
NU, | KAK \VECT OR = VECT UM ;VEHEND" | PERENESENIE TO^KI IZ NA^ALXNOGO POLOVENIQ W KONE^NOE (LAT. veStor | NESU]IJ).

10
\The more general expression of algebra, a1+p;1a2 , for any (so called) imaginary root of a quadratic or other equation, : : : interpreted as being a symbol of the number-couple which I had otherwise denoted by (a1 a2) : : :
its multiplication by another number-couple is expressed by the formula
(b1 b2)(a1 a2) = (b1a1 ;b2a2 b2a1 +b1a2)" ([35], p. 12).
w REZULXTATE [IROKO RASPROSTRANILOSX IMENNO TAKOE OPREDELENIE
KOMPLEKSNYH ^ISEL | KAK UPORQDO^ENNYH PAR (a b) DEJSTWITELXNYH ^ISEL S OPERACIQMI IH SLOVENIQ I UMNOVENIQ PO FORMULAM:
(a b)+(c d) = (a+c b+d) (a b)(c d) = (ac;bd ad+bc).
fORMALXNU@ BEZUPRE^NOSTX \TOGO OPREDELENIQ NESKOLXKO PORTIT WOZNIKA@]IJ TERMINOLOGI^ESKIJ KAZUS: POSKOLXKU TERMIN \KOMPLEKS- NYE ^ISLA" OB_EDINQET ^ISLA DEJSTWITELXNYE I MNIMYE, PRINIMAQ DANNOE OPREDELENIE, PRIHODITSQ DELATX NE UKRA[A@]IJ MATEMATIKU
WYWOD: L@BOE DEJSTWITELXNOE ^ISLO ESTX UPORQDO^ENNAQ PARA DEJSTWITELXNYH ^ISEL.
aLGEBRAI^ESKOE OPREDELENIE KOMPLEKSNYH ^ISEL, NE SWQ-
ZANNOE S IH NAGLQDNYM PREDSTAWLENIEM, MOVET BYTX DANO SLEDU@]IM OBRAZOM.
sISTEMA KOMPLEKSNYH ^ISEL C ESTX REZULXTAT PRISOEDINENIQ K SISTEME DEJSTWITELXNYH ^ISEL R NE SODERVA-
]EGOSQ W NEJ \LEMENTA i, PO OPREDELENI@ OBLADA@]EGO SWOJ- STWOM i2 =;1. nA WOZNIKA@]IE W HODE \TOGO PRISOEDINENIQ1 SO^ETANIQ a+ib (^ISEL a b2R I \LEMENTA i), POLU^IW[IE NAZWANIE KOMPLEKSNYH ^ISEL , RASPROSTRANQ@TSQ DEJSTWIQ
SLOVENIQ, WY^ITANIQ, UMNOVENIQ I DELENIQ3 S REZULXTA-
TAMI (^TO SU]ESTWENNO) W WIDE TAKIH VE SO^ETANIJ (c. 9).
sUDITX O TOM, KAKOJ SPOSOB WWEDENIQ KOMPLEKSNYH ^ISEL PREDPO-
^TITELXNEJ | ALGEBRAI^ESKIJ ILI GEOMETRI^ESKIJ, | SLEDUET S U^E-
1 t. E. RASPROSTRANENIQ NA \LEMENT i IME@]IHSQ W SISTEME R OPERA- CIJ SLOVENIQ I UMNOVENIQ S SOHRANENIEM IH PRIWY^NYH \ZAKONOW".
2 s WOZMOVNOSTX@ PERESTANOWOK W NIH SLAGAEMYH I SOMNOVITELEJ,
ZAPISX@ a;ib WMESTO a+i(;b) I SOKRA]ENIQMI a+i0=a 0+ib=ib. 3 pO TEM VE PRAWILAM, KAK ESLI BY \LEMENT i BYL DEJSTWITELXNOJ
PEREMENNOJ S DOPOLNITELXNYM SWOJSTWOM i2 =;1.
