
Шведенко Начала анализа функций комплексной переменной 2008
.pdf
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
171 |
|
MNOVESTWE SOWOKUPNOGO IZMENENIQ PEREMENNYH 2 |
; ! 2C . |
|||||||||||||||||||||||||||||||||||||||
|
|TIM USTANOWLENO, ^TO DLQ L@BOJ TO^KI |
|
z OBLASTI D |
|||||||||||||||||||||||||||||||||||||
SU]ESTWUET |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
; |
( z)d |
|
= lim |
|
|
|
; |
|
|
|
|
|
|
|
; |
|
|
|
|
( z)d |
|
= |
||||||||||||||||||
|
|
|
( z+ |
z)d |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
Mz!0 Mz |
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
R |
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
z d |
|
|
|
Q.E.D. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
) . |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
zAWER[ITX DOKAZATELXSTWO TEOREMYRMOVNO POSLEDOWATELX- |
|||||||||||||||||||||||||||||||||||||||
NYM PRIMENENIEM DOKAZANNOJ LEMMY, POLAGAQ NA PERWOM |
||||||||||||||||||||||||||||||||||||||||
[AGE W EE USLOWII |
|
|
( z) = |
1 |
'( ) 1 |
I POLU^AQ (POWTORNO, |
||||||||||||||||||||||||||||||||||
|
|
2 i ;z |
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
NO NA SEJ RAZ KAK SLEDSTWIE LEMMY) REZULXTAT: |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
1 |
'( ) |
|
0 |
1 |
|
|
|
|
'( ) |
0 |
|
|
|
|
|
|
|
1! |
|
|
|
'( ) |
|
||||||||||||||
|
f0(z) = 2 i ; ;z d = |
2 i ; |
;z d |
|
= |
|
2 i ; ( ;z)2 d. |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
||
|
rASSUVDAQ DALEE PO INDUKCII, T. E. S^ITAQ UVE USTANOW- |
|||||||||||||||||||||||||||||||||||||||
LENNYM FAKT SU]ESTWOWANIQ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
f(k;1)(z) = |
(k;1)! |
|
|
'( ) |
|
d, |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 i |
|
|
; |
( |
;z) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
DOSTATO^NO PRIMENITX LEMMU S R ( z) = |
(k;1)! '( ) k |
, DOKA- |
||||||||||||||||||||||||||||||||||||||
ZAW W REZULXTATE SU]ESTWOWANIE |
|
|
|
|
|
|
|
|
|
|
|
|
2 i ( ;z) |
|||||||||||||||||||||||||||
f(k)(z) = (k;1)! |
|
|
'( ) |
d 0= (k;1)! |
|
|
|
|
|
'( ) |
|
0d |
= |
|
|
|||||||||||||||||||||||||
|
|
k |
|
|
|
|
|
|
k |
|
|
|||||||||||||||||||||||||||||
|
|
|
2 i ; ( ;z) |
|
|
|
|
2 i |
; ( ;z) |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
'( ) |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
k! |
|
|
|
|
|
|
d. Q.E.D. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 i |
|
|
|
( ;z) |
k+1 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
||
sOEDINENIE DOKAZANNOJ TEOREMY I INTEGRALXNOJ FORMU-
LY kO[I PRIWODIT K SLEDU@]EMU FUNDAMENTALXNOMU SWOJ-
STWU ANALITI^ESKIH FUNKCIJ.
1 s^ITAQ, ^TO PROBEGAET KONTUR ;, A z | L@BU@ NE PERESEKA@-
]U@SQ S NIM OBLASTX D.

172
tEOREMA O PROIZWODNYH ANALITI^ESKOJ FUNKCII. eSLI FUNKCIQ w =f(z) QWLQETSQ ANALITI^ESKOJ W OBLASTI
|
|
C (T. E. IMEET PROIZWODNU@ f0(z) W L@BOJ TO^Ke z |
2 |
1 |
|||||||||
D |
|
|
|
|
D), |
||||||||
TO ONA IMEET W OBLASTI D PROIZWODNYE WSEH PORQDKOW W |
|||||||||||||
SLU^AE, ESLI OBLASTX D QWLQETSQ ODNOSWQZNOJ, SPRAWEDLIWA |
|||||||||||||
FORMULA kO[I DLQ PROIZWODNYH |
: |
|
|
||||||||||
|
(k) |
|
|
|
|
k! |
H |
f( ) |
|
|
|
||
f |
|
|
(z) ind(; z) = 2 i |
( ;z)k+1 d, z 2D k = 1 2 : : : , |
|||||||||
|
|
; |
|||||||||||
GDE W KA^ESTWE ; MOVET BYTX WZQT L@BOJ NE PROHODQ]IJ |
|||||||||||||
^EREZ TO^KU z 2D ZAMKNUTYJ KUSO^NO-GLADKIJ KONTUR, CE- |
|||||||||||||
LIKOM RASPOLOVENNYJ W OBLASTI D. |
|
|
|||||||||||
|
|
dOKAZATELXSTWO |
. dLQ PROIZWOLXNO WZQTOJ TO^KI z OB- |
||||||||||
LASTI D PUSTX |
K | KRUG S CENTROM z, PRINADLEVA]IJ |
||||||||||||
\TOJ OBLASTI, a |
C | L@BAQ KONCENTRI^ESKAQ OKRUVNOSTX |
||||||||||||
MENX[EGO RADIUSA. pRIMENENIE K ANALITI^ESKOJ FUNKCII w = f(z) W KRUGE K (A NE WO WSEJ OBLASTI D, KOTORAQ MO-
VET BYTX NEODNOSWQZNOJ) INTEGRALXNOJ FORMULY kO[I S
OKRUVNOSTX@ C W KA^ESTWE KONTURA (S^ITAQ EE ODNOKRAT-
NO OBHODIMOJ W POLOVITELXNOM NAPRAWLENII) DAET PREDSTAWLENIE \TOJ FUNKCII WNUTRI OKRUVNOSTI C W WIDE IN-
|
|
H |
f( ) |
|
|
|
|
|
|
|
|
;z d, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
TEGRALA kO[I: f(z)= 21iC |
z 2int C. oSTAETSQ PRI- |
||||||||
MENITX TEOREMU O PROIZWODNYH INTEGRALA kO[I: PRAWAQ (A |
|||||||||
POTOMU I LEWAQ) ^ASTX POSLEDNEJ FORMULY IMEET WNUTRI |
|||||||||
OKRUVNOSTI C (S CENTROM W PROIZWOLXNO WZQTOJ TO^KE OBLAS- |
|||||||||
TI D) PROIZWODNYE WSEH PORQDKOW f(k)(z)= |
k! |
|
'( ) |
d. |
|||||
2 i |
|
( ;z) |
k+1 |
||||||
|
|
|
|
|
C |
|
|
||
w SLU^AE ODNOSWQZNOJ OBLASTI |
D WMESTO ROKRUVNOSTI |
||||||||
1 w \TOM SOSTOIT PRINCIPIALXNOE RAZLI^IE FUNKCIJ DEJSTWITELX- NOJ I KOMPLEKSNOJ PEREMENNYH: FUNKCIQ DEJSTWITELXNOJ PEREMENNOJ MOVET IMETX NA INTERWALE (OBLASTI NA PRQMOJ) PERWU@ PROIZWODNU@,
NO NE IMETX SLEDU@]IH (PRIMER: y = xjxj c y0 = 2jxj).

173
C (S CENTROM W PROIZWOLXNO WZQTOJ TO^KE z 2 D) MOVNO WZQTX L@BOJ (NE PROHODQ]IJ ^EREZ \TU TO^KU) ZAMKNUTYJ KUSO^NO-GLADKIJ KONTUR ; D I, PRIMENIW WNA^ALE INTEG-
RALXNU@ FORMULU kO[I, A ZATEM TEOREMU O PROIZWODNYH INTEGRALA kO[I S U^ETOM SWOJSTWA POSTOQNSTWA INDEKSA
ZAMKNUTOGO KONTURA1, POSLEDOWATELXNO POLU^ITX:
|
|
|
|
|
1 |
|
f( ) |
|
|
|
||
|
f(z) ind(; z) = |
; ;z d , |
|
|
|
|||||||
|
2 i |
|
|
|
||||||||
(k) |
|
k! |
H |
f( ) |
|
|
H |
|
|
|
|
|
f (z) ind(; z) = 2 i |
( ;z)k+1 d , k = 1 2 : : : |
Q.E.D. |
||||||||||
; |
||||||||||||
tEOREMA mORERY.2 |
eSLI W OBLASTI3 D C |
FUNKCIQ |
||||||||||
w = f(z) |
NEPRERYWNA I DLQ L@BOGO ZAMKNUTOGO KUSO^NO- |
|||||||||||
GLADKOGO KONTURA ; (LEVA]EGO W OBLASTI D) |
H |
f |
(z)dz = 0 4 |
|||||||||
|
||||||||||||
;
TO FUNKCIQ w =f(z) QWLQETSQ ANALITI^ESKOJ W OBLASTI D.
dOKAZATELXSTWO. eSLI WYPOLNENY USLOWIQ TEOREMY, TO W SI-
LU LEMMY O SU]ESTWOWANII PERWOOBRAZNOJ (X, c. 159) FUNKCIQ
w =f(z) IMEET W OBLASTI D PERWOOBRAZNU@: f(z)= '0(z) |
z 2 D. |
|||||
|
= |
( ), |
|
0( ) = |
( ), |
|
fUNKCIQ w |
|
' z |
IMEQ W OBLASTI D PROIZWODNU@ ' |
z |
|
f z |
QWLQETSQ ANALITI^ESKOJ W \TOJ OBLASTI I PO TEOREME O PROIZ-
WODNYH ANALITI^ESKOJ FUNKCII (S. 172) IMEET W NEJ PROIZWODNYE
WSEH PORQDKOW. sLEDOWATELXNO, PROIZWODNYE WSEH PORQDKOW IMEET W OBLASTI D I FUNKCIQ w = f(z)= '0(z). Q.E.D.
1 w L@BOJ OBLASTI, NE SODERVA]EJ TO^EK \TOGO KONTURA (IX, c. 141), A SLEDOWATELXNO, W OKRESTNOSTI KAVDOJ NE LEVA]EJ NA NEM TO^KI.
2 iTALXQNSKIJ MATEMATIK mORERA (Morera, Giacinto, 1856{1909) OPUBLIKOWAL EE W 1886 G. (W Rendiconti Reale Istituto Lombardo, ser. II,
t. XIX, p. 304{307) KAK \OBRATNU@ K TEOREME kO[I" (\l'inverso del
teorema di Cauchy").
3 nE OBQZATELXNO ODNOSWQZNOJ.
4 nA SAMOM DELE DOSTATO^NO, ^TOBY RAWNQLSQ NUL@ INTEGRAL \TOJ FUNKCII PO L@BOJ ZAMKNUTOJ LOMANOJ W OBLASTI D.

174
pOSLEDOWATELXNOSTX FUNKCIJ ffn(z)g S^ITA@T1 SHODQ]EJSQ RAWNOMERNO WNUTRI OBLASTI D K FUNKCII w = f(z), ESLI DLQ L@BOGO ZAMKNUTOGO KRUGA K D I L@BOGO POLOVITELXNOGO
^ISLA " SU]ESTWUET TAKOE (ZAWISQ]EE OT KRUGA K I ^ISLA ")
NATURALXNOE ^ISLO n0 , ^TO PRI n>n0 NERAWENSTWO jfn(z);f(z)j<
" OKAZYWAETSQ WYPOLNENNYM SRAZU DLQ WSEH TO^EK z 2K. sIMWOLI^ESKI DANNOE OPREDELENIE WYRAVAETSQ FORMULOJ
8z0 8r >0;(z0 2D ^ 8z (jz;z0j6r =) z 2D)) =)
=) 8">0 9n0 8n 8z (n>n0 ^ jz;z0j6r =) jfn(z);f(z)j<") .
tEOREMA wEJER[TRASSA (O POSLEDOWATELXNOSTQH ANALITI^ESKIH FUNKCIJ).2 eSLI POSLEDOWATELXNOSTX ffn(z)g FUNKCIJ, ANALITI^ESKIH W OBLASTI D, SHODITSQ RAWNOMERNO WNUTRI \TOJ OBLASTI K FUNKCII w=f(z), TO
a) w=f(z) | ANALITI^ESKAQ FUNKCIQ W OBLASTI D B) DLQ L@BOGO k = 1 2 : : : POSLEDOWATELXNOSTX PROIZ-
WODNYH ff(k)(z)g SHODITSQ K PROIZWODNOJ f(k)(z) PREDELXNOJ
n
FUNKCII RAWNOMERNO WNUTRI OBLASTI D.
dOKAZATELXSTWO. pUSTX K0
OBLASTI D KRUG, z0 | EGO CENTR, K | ZAMKNUTYJ KON-
CENTRI^ESKIJ KRUG MENX[EGO RADIUSA, C | OGRANI^IWA@- ]AQ KRUG K OKRUVNOSTX (RIS. 65, a). B SILU NERAWENSTWA jfn(z);f(z)j<" ;WYPOLNQ@]EGOSQ DLQ WSEH TO^EK z 2 K PRI n>n0(K ") I NERAWENSTWA
jf(z);f( )j 6 jf(z);fn(z)j + jfn(z);fn( )j + jfn( );f( )j
1 oSNOWYWAQSX NA OPREDELENII wEJER[TRASSA TOGO, ^TO RQD +1 fn(z)
P
n=0
(T. E. POSLEDOWATELXNOSTX f0(z) f0(z) + f1(z) f0(z) +f1 (z) + f2(z) : : : )
FUNKCIJ SHODITSQ RAWNOMERNO W OKRESTNOSTI TO^KI a (\die Reihe
convergire gleichmassig in der Nahe der Stelle a" [43], Bd. 2, S. 201{202).
2 pERWONA^ALXNYJ EE WARIANT BYL POLU^EN wEJER[TRASSOM W 1841 G. ([43], Bd. 1, S. 73{74).

175
rIS. 65
PREDELXNAQ FUNKCIQ w =f(z) NEPRERYWNA W KRUGE K (A ZNA-
^IT, I NA OKRUVNOSTI C), PO\TOMU DLQ USTANOWLENIQ ANALITI^NOSTI \TOJ FUNKCII W TO^KE z0 DOSTATO^NO PROWERITX
1 f( )
2 iH ;z d WNUTRI OKRUVNOSTI
C
C (S^ITAQ EE ODNOKRATNO OBHODIMOJ W POLOVITELXNOM NAPRAW-
LENII). w SILU INTEGRALXNOJ FORMULY kO[I, PRIMENENNOJ K
FUNKCIQM w = fn(z) W KRUGE K0 |
I TO^KAM z c |
jz ;z0j < r (r | |
||||||||||||||||||||||||||||||||||||
RADIUS OKRUVNOSTI C), A TAKVE WYPOLNQ@]EGOSQ DLQ WSEH TO^EK |
||||||||||||||||||||||||||||||||||||||
z 2 K PRI n>n0(K ") NERAWENSTWA |
jfn(z);f(z)j<" \TU PROWERKU |
|||||||||||||||||||||||||||||||||||||
DAET OCENKA INTEGRALA PO KONTURU (VIII, c. 133): |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
f( ) d |
|
= |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
f( );fn ( ) d |
|
6 |
|
|
|||||||||
|
6 |
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d 6 |
;z |
|
|
|
|
|
|
|
||||||||||||
|
|
f(z) ; 2 i C ;z |
|
|
|
f(z);fn(z); 2 i C |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
H |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
H |
n |
|
|
|
|
|
|
|
|
|
|
1 |
|
"2 r |
|
|
||||
|
|
|
|
|
f(z) ; fn(z) + |
|
|
|
|
|
|
|
( ;z0);(z;z0) |
|
|
" + 2 r;jz;z0j . |
||||||||||||||||||||||
|
|
|
|
|
|
|
2 i C |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
dLQ L@BOGO ZAMKNUTOGO KRUGA K |
|
|
D PUSTX C | KON- |
|||||||||||||||||||||||||||||||||
CENTRI^ESKAQ OKRUVNOSTX BOLX[EGO RADIUSA, TAKVE PRI- |
||||||||||||||||||||||||||||||||||||||
NADLEVA]AQ (S OGRANI^IWAEMYM E@ KRUGOM) OBLASTIe |
|
D |
||||||||||||||||||||||||||||||||||||
( |
|
|
. 65, |
|
|
|
|
; |
|
|
fn(z) |
! f(z) |
|
|
|
|
|
|
|
|
|
|
|
|
2 e |
|||||||||||||
|
RIS |
|
|
|
B |
|
tAK KAK |
|
|
|
|
|
|
|
|
|
|
|
|
RAWNOMERNO WNUTRI OB |
||||||||||||||||||
LASTI |
D, fn( ) f( ) <" |
ODNOWREMENNO DLQ WSEH TO^EK |
C |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||

176
PRI n > n0(C "), IZ ^EGO S PRIMENENIEM FORMUL kO[I DLQ
PROIZWODNYH (c. 172) I OCENKI INTEGRALA (VIII, c. 133) SLE- |
|||||||||||||||||||||||||
|
|
|
|
, |
|
e |
|
|
z 2K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
DUET |
|
^TO DLQ TO^EK |
|
|
H |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
(k) |
|
(k) |
|
|
k |
fn( );f( ) d |
|
|
|
k!2 r |
|
|
" |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
e |
|
< 2 (r; )k+1 |
|
|
||||||||||||
|
|
fn (z) ; f (z) = |
2 i |
( ;z)k+1 |
|
|
|
|
|||||||||||||||||
|
|
|
C |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
C |
(ZDESX r I | RADIUSY SOOTWETSTWENNO OKRUVNOSTI C |
|
I |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
KRUGA K). |
Q.E.D. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
uPRAVNENIQ. |
1. dOKAZATX, ^TO ESLI NEPRERYWNAQ W OBLASTI D |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
FUNKCIQ w =f(z) OBLADAET TEM SWOJSTWOM, |
^TO |
|
f(z)dz = 0 |
DLQ L@BOGO |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
PRQMOLINEJNOGO OTREZKA L |
|
D, TO f(z) |
|
0 |
W OBLASTI D. |
|
|
|
|
|
|||||||||||||||
|
|
|
2. dOKAZATX SLEDU@]IJ USILENNYJ WARIANT TEOREMY mORERY. |
|
|
||||||||||||||||||||
|
ESLI FUNKCIQ w =f(z) |
NEPRERYWNA W OBLASTI D C |
|
I |
H |
f(z)dz = 0 |
|||||||||||||||||||
|
|
||||||||||||||||||||||||
|
|
T |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
T , TO \TA |
||||
|
DLQ L@BOGO (RASPOLOVENNOGO W OBLASTI D) TREUGOLXNIKA |
|
|||||||||||||||||||||||
|
FUNKCIQ QWLQETSQ ANALITI^ESKOJ W OBLASTI D. |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
3. dOKAZATX SLEDU@]IJ FAKT, IZWESTNYJ KAK TEOREMA lIUWILLQ |
2. |
|||||||||||||||||||||
eSLI CELAQ (T, E. ANALITI^ESKAQ WO WSEJ PLOSKOSTI C ) FUNKCIQ QW-
LQETSQ OGRANI^ENNOJ, TO \TA FUNKCIQ POSTOQNNA.
|
H |
uKAZANIE: DLQ PROIZWOLXNO WZQTOJ TO^KI z C |
OCENITX INTEGRAL |
|||||||
|
f;( ) |
d PO OKRUVNOSTI Cr RADIUSA |
r PRI r2 |
+ |
1 |
, a ZATEM PRI- |
||||
|
|
( z)2 |
||||||||
Cr |
; |
|
|
|
|
! |
|
|
||
|
MENITX FORMULU kO[I DLQ PROIZWODNOJ (c. 172) I PERWOE IZ USLOWIJ |
|||||||||
|
POSTOQNSTWA ANALITI^ESKOJ FUNKCII W OBLASTI (VII, c. 112). |
|||||||||
|
|
|
|
|||||||
|
|
1 sLEDUET OTMETITX, ^TO W SLU^AE NEODNOSWQZNOJ OBLASTI D IZ \TO- |
||||||||
|
GO NE SLEDUET, ^TO |
H |
f(z)dz = 0 DLQ L@BOJ ZAMKNUTOJ LOMANOJ P , |
|||||||
|
|
|
|
P |
|
|
|
|
|
|
|
RASPOLOVENNOJ W OBLASTI D (X, UPRAVNENIE NA S. 164). |
|
||||||||
|
|
2 fRANCUZSKIJ MATEMATIK lIUWILLX |
(Liouville, Joseph, 1809{1882) |
|||||||
OPUBLIKOWAL \TU TEOREMU W 1844 G. sWOE NEDOWOLXSTWO \TIM NEODNOKRAT-
NO WYRAVAL kO[I ([28], ser. I, t. VIII, p. 378 t. XI, p. 374), S^ITAW[IJ SEBQ AWTOROM \TOJ TEOREMY.
177
XII. kAK OPERIRU@T TEOREMOJ I INTEGRALXNOJ FORMULOJ kO[I I ^TO UTWERVDA@T TEOREMY tEJLORA I lORANA
oBY^NYM PREPQTSTWIEM K PRAKTI^ESKOMU PRIMENENI@
TEOREMY kO[I (RAWNO KAK I EE SLEDSTWIQ | INTEGRALXNOJ FORMULY kO[I) WYSTUPAET NEODNOSWQZNOSTX OBLASTI, PO KOTOROJ PROHODIT KONTUR INTEGRIROWANIQ (I W KOTOROJ POD- YNTEGRALXNAQ FUNKCIQ QWLQETSQ ANALITI^ESKOJ.
wSTRE^A@]IESQ W LITERATURE POPYTKI RASPROSTRANITX TEOREMU kO[I NA MNOGOSWQZNYE OBLASTI (OB]EGO WIDA) NEIZMENNO PRIWODQT K UTWERVDENIQM ^ASTNOGO HARAKTERA: W KA^ESTWE MNOGOSWQZNOJ OBLASTI W NIH WYSTUPAET KONKRETNAQ EE RAZNOWIDNOSTX, RAWNO KAK KONKRETNYM PREDSTAWLQETSQ I RASPOLOVENNYJ W NEJ KONTUR INTEGRIROWANIQ.
nEWOZMOVNOSTX PRQMOGO PRIMENENIQ TEOREMY kO[I I
INTEGRALXNOJ FORMULY kO[I K INTEGRALAM FUNKCIJ W NEOD-
NOSWQZNYH OBLASTQH WOWSE NE OZNA^AET, ^TO \TO ZATRUDNENIE NELXZQ OBOJTI.
nAIBOLEE PROSTYM OKAZYWAETSQ SLU^AJ, KOGDA W ISHODNOJ
NEODNOSWQZNOJ OBLASTI D C (W KOTOROJ LEVIT KONTUR IN-
TEGRIROWANIQ, A PODYNTEGRALXNAQ FUNKCIQ QWLQETSQ ANALITI^ESKOJ) UDAETSQ WYDELITX ODNOSWQZNU@ OBLASTX D1 D, CELIKOM SODERVA]U@ KONTUR INTEGRIROWANIQ ;: SLEDUET LI[X NA WREMQ ZABYTX PRO ISHODNU@ OBLASTX D I DEJSTWO- WATX ISKL@^ITELXNO W RAMKAH ODNOSWQZNOJ OBLaSTI D1 .
~A]E VE WYHOD IZ ZATRUDNENIQ NAHODQT W PREOBRAZOWA- NII KONTURA INTEGRIROWANIQ | ZAMENE EGO (CELIKOM ILI PO U^ASTKAM) DRUGIM, NO S TEM VE ZNA^ENIEM INTEGRALA. pRIMEROM PRIMENENIQ \TOGO PRIEMA MOVET SLUVITX DOKA- ZATELXSTWO SLEDU@]EGO UTWERVDENIQ | WARIANTA TEOREMY kO[I DLQ PROSTEJ[EJ NEODNOSWQZNOJ OBLASTI.
178
TEOREMa kO[I DLQ KOLXCA.1 |
eSLI FUNKCIQ w = f(z) |
||||
QWLQETSQ ANALITI^ESKOJ W KOLXCE |
|
||||
A = |
|
z 2C : r1 <jz;z0j<r2 06r1 <r2 6+1,2 |
|||
TO EE INTEGRAL |
R |
f(z)dz PO L@BOMU |
(RASPOLOVENNOMU W \TOM |
||
;
KOLXCE) ZAMKNUTOMU KUSO^NO-GLADKOMU KONTURU ; ZAWISIT
LI[X OT INDEKSA |
\TOGO KONTURA OTNOSITELXNO |
CENTRA z0 KOLX- |
||||
CA. a IMENNO, |
H |
f(z)dz = ind(; z0) |
H |
f(z)dz |
, GDE |
C | L@BAQ |
|
; |
C |
|
|
|
|
|
|
|
|
|
|
|
(LEVA]AQ W \TOM KOLXCE) OKRUVNOSTX S CENTROM z0, ODIN RAZ OBHODIMAQ W POLOVITELXNOM NAPRAWLENII (RIS. 66, a)3.
|
dOKAZATELXSTWO. |
|
pUSTX z1 | L@BAQ TO^KA KONTURA ; |
|||||||||||
|
|
|||||||||||||
(WYBRANNAQ NA^ALXNOJ)4, |
L1 |
| PRQMAQ, PROHODQ]AQ ^EREZ |
||||||||||||
TO^KI z0 I z1 , |
L2 | PRQMAQ, PERESEKA@]AQ W TO^KE z0 PRQ- |
|||||||||||||
MU@ L1 (DLQ OPREDELENNOSTI POD PRQMYM UGLOM RIS. 66, B). |
||||||||||||||
|
ESLI KONTUR ; NE IMEET OB]IH TO^EK S PRQMOJ L2 , TO |
|||||||||||||
UTWERVDENIE TEOREMY WERNO, TAK KAK ODNOWREMENNO |
||||||||||||||
|
|
|
def |
|
1 |
|
|
|
dz |
|
|
|
|
|
|
ind(; z0) = |
|
2 i |
; |
|
z;z0 |
= 0 I |
; |
f(z)dz = 0 |
|||||
W SILU TEOREMY kO[I, |
H |
|
|
|
H |
|
||||||||
PRIMENENNOJ K ANALITI^ESKIM FUNK- |
||||||||||||||
CIQM w = |
1 |
I w = f(z) W ODNOSWQZNOJ OBLASTI | POLU- |
||||||||||||
z;z0 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
KOLXCE, \OTREZAEMOM" OT KOLXCA A PRQMOJ L2 . |
||||||||||||||
|
|
|
|
|||||||||||
1 u kO[I W [28], ser. I, t. VIII, p. 162{163. |
|
|
||||||||||||
2 pRI r1 = 0 I r2 < +1 |
\TO KOLXCO ESTX KRUG S IZ_QTYM CENTROM |
|||||||||||||
z0, PRI r1 > 0 I r2 = +1 |
| WNE[NOSTX OKRUVNOSTI, A PRI r1 = 0 I |
|||||||||||||
r2 = +1 | PLOSKOSTX C |
S IZ_QTOJ TO^KOJ z0 (oBOZNA^ENIE KOLXCA |
|||||||||||||
A | PO NA^ALXNOJ BUKWE FR. anneau | KOLXCO).
3 oKRUVNOSTX C | ^TOBY NE ZAGROMOVDATX RISUNOK | IZOBRAVENA NE PERESEKA@]EJ KONTUR ;, A \TOT KONTUR | ODNOKRATNO OBHODQ]IM
CENTR KOLXCA W POLOVITELXNOM NAPRAWLENII.
4 OT EE WYBORA ZNA^ENIE Hf(z)dz NE ZAWISIT (VIII, c. 128).
;
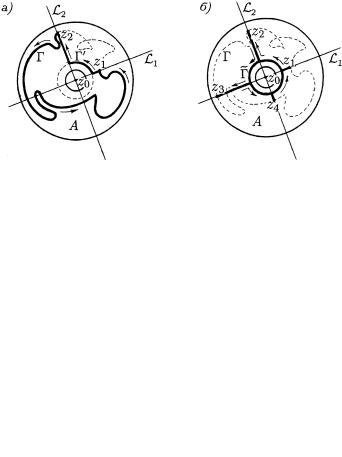
179
rIS. 66
eSLI VE KONTUR ; IMEET OB]IE TO^KI S PRQMOJ L2 (KAK NA RIS. 66, B), TO PUSTX z2 | PERWAQ IZ NIH (W PORQDKE SLEDOWANIQ TO^EK KONTURA ; OT TO^KI
rIS. 67
pRIMENQQ TEOREMU kO[I (X, S. 151) K FUNKCII w = f(z) W ODNOSWQZNOJ OBLASTI | KOLXCE A S \RAZREZOM" PO LU^U IZ
TO^KI z0 WDOLX PRQMOJ L1 W NAPRAWLENII, PROTIWOPOLOVNOM NAPRAWLENI@ NA TO^KU z1 , MOVNO SDELATX WYWOD: ZNA^ENIQ
H |
I |
ind(; z0) NE IZMENQTSQ, ESLI U^ASTOK KONTURA |
f(z)dz |
||
; |
|
|

180
; OT TO^KI z1 DO TO^KI z2 ZAMENITX KUSO^NO-GLADKIM KON-
TUROM, SOSTOQ]IM IZ OTREZKOW PRQMYH |
L1 L2 , SOEDINQ@- |
|||
]IH TO^KI z1 I z2 S OKRUVNOSTX@ C, |
I ^ETWERTI \TOJ |
|||
OKRUVNOSTI (RIS. 67, A). |
|
|
|
|
dEJSTWIQ PO \TOJ SHEME (PRI KOTOROJ PRQMYE L1 I |
L2 |
|||
POPEREMENNO MENQ@TSQ ROLQMI) PREOBRAZU@T KONTUR ; |
| S |
|||
SOHRANENIEM ZNA^ENIJ |
H |
f(z)dz I ind(; z0) | W SOSTOQ]IJ |
||
|
; |
|
|
|
IZ ^ETWERTEJ OKRUVNOSTI C, SOEDINENNYH OTREZKAMI PRQ- |
||||
MYH L1 I L2 (RIS. 67, B). pOSKOLXKU KAVDYJ IZ \TIH OTREZ- |
||||
KOW OBHODITSQ DWAVDY W PROTIWOPOLOVNYH NAPRAWLENIQH, |
||||
INTEGRAL PO \TOMU KONTURU RAWEN INTEGRALU PO OKRUVNOS- |
||||
TI C, OBHODIMOJ STOLXKO VE RAZ, KAKOW ind(; z0). Q.E.D. |
||||||||
tEOREMA tEJLORA.1 |
fUNKCIQ w = f(z), ANALITI^ESKAQ |
|||||||
|
D = |
|
z 2 |
|
+1 |
|
|
2 IMEET W \TOM KRUGE |
W KRUGE |
|
|
|
C |
|
|
|
|
PREDSTAWLENIE W WIDE SUMMY SHODQ]EGOSQ STEPENNOGO RQDA |
||||||||
|
|
|
|
|
P |
|
|
|
|
|
|
f(z) =n=0cn(z;z0)n z 2D, |
|||||
KO\FFICIENTY KOTOROGO SWQZANY S NEJ SOOTNO[ENIQMI3 |
||||||||
cn = |
f(n)(z0) |
I cn = |
1 |
|
f( ) |
|
||
n! |
|
|
n+1 d , n=0 1 2 : : : , |
|||||
|
|
|
|
2 i ( ;z0) |
|
|||
GDE ; | L@BOJ ZAMKNUTYJH;KUSO^NO-GLADKIJ KONTUR, RASPO-
LOVENNYJ W KRUGE D I ODIN RAZ OBHODQ]IJ EGO CENTR z0 W
POLOVITELXNOM NAPRAWLENII (RIS. 68, A).
1 nAZWANIE USLOWNO: \TU TEOREMU (USTANOWLENNU@ kO[I W 1831 G.
DLQ SLU^AQ z0 = 0 [28], ser. II, t. XV, p. 448{450) PRAWILXNEE NAZYWATX
TEOREMOJ kO[I O RAZLOVENII ANALITI^ESKOJ FUNKCII W RQD tEJLORA. pO UDIWITELXNO ^ASTOMU POWTORENI@ EE FORMULIROWKI W RABOTAH kO[I RAZNOGO WREMENI MOVNO SDELATX WYWOD, ^TO IMENNO EE (A NE TO, ^TO NYNE NAZYWA@T TEOREMOJ kO[I) ON S^ITAL GLAWNYM SWOIM REZULXTATOM.
2 wKL@^AQ SLU^AJ r =+1, KOGDA KRUG D ESTX WSQ PLOSKOSTX C .
3 pERWOE IZ KOTORYH I OZNA^AET, ^TO \TOT STEPENNOJ RQD QWLQETSQ FUNKCII w=f(z) (II, S. 33).
