
Шведенко Начала анализа функций комплексной переменной 2008
.pdf
241
dOKAZATELXSTWO. pUSTX | L@BAQ OTLI^NAQ OT z1 z 2 : : :
TO^KA PLOSKOSTI C , A n | NASTOLXKO BOLX[OE NATURALXNOE
^ISLO, ^TO 2 int;n (SWOJSTWO 2 ). pRIMENENIE TEOREMY O
WY^ETAH K KONTURNOMU INTEGRALU H f(z) dz W ODNOSWQZNOJ
;n z;
OBLASTI int;n+1 (W SILU SWOJSTWA 2 SODERVA]EJ KONTUR ;n) DAET W SO^ETANII S DOKAZANNOJ LEMMOJ:
|
1 |
|
f(z) |
dz = res |
f(z) |
+ |
|
|
|
res |
f(z) |
= f( ) |
;zj |
|
gj( ). |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
2 i |
z |
; |
|
|
z= |
z |
; |
|
|
zj |
|
int;nz=zj z |
; |
|
|
|
|
int;n |
|
||||||||||
|
;Hn |
|
|
|
|
|
|
|
|
|
2P |
|
|
|
|
|
|
|
|
|
|
2P |
|
|||||||
|
oSTAETSQ PRIMENITX K LEWOJ ^ASTI RAWENSTWA OCENKU IN- |
|||||||||||||||||||||||||||||
TEGRALA (VIII, S. 133), IZ KOTOROJ S U^ETOM SWOJSTW 2 I 3 |
||||||||||||||||||||||||||||||
WYTEKAET, |
^TO |
1 |
|
|
f(z) dz |
|
|
|
0, |
|
A SLEDOWATELXNO, |
|
||||||||||||||||||
2 i |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
z |
|
|
|
n |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
;Hn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
; |
|
|
|
;! |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
! 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
f( ) = +1gj( ) |
|
|
C =z1 z2 : : : , |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
j=1 |
|
|
|
|
|
2 |
|
|
|
|
6 |
|
|
|
|
|
|
||||||
ESLI PRAWU@ ^ASTX PONIMATX KAK |
|
|
lim |
|
|
|
gj( ). Q.E.D. |
|||||||||||||||||||||||
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
+ |
|
|
zj |
int;n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
! |
|
|
1 |
|
2P |
|
|
|
|
||
sU]ESTWENNO, ^TO IZLOVENNYJ SPOSOB RAZLOVENIQ PRI- MENIM I K MEROMORFNYM FUNKCIQM w =f(z), UDOWLETWORQ@-
]IM BOLEE SLABOMU, NEVELI 3 , USLOWI@
3e supjz;mf(z)j ;! 0 PRI NEKOTOROM NATURALXNOM m
z2;n n!+1
DOSTATO^NO PEREJTI K WSPOMOGATELXNOJ MEROMORFNOJ FUNK-
CII w=z;mf(z), POLU^ITX EE RAZLOVENIE z;mf(z)=+P1gj(z)
j=1
W RQD PROSTYH DROBEJ I IZ NEGO RAZLOVENIE f(z)= +1zmgk(z)
kP=1
ISHODNOJ MEROMORFNOJ FUNKCII W RQD RACIONALXNYH (S PO- SLEDU@]IM RAZLOVENIEM IH NA PROSTYE)1.
1 bOLEE RASPROSTRANENNYJ PRIEM RAZLOVENIQ MEROMORFNYH FUNK- CIJ SO SWOJSTWOM 3e, IZLOVEN W [4], GL. VI, x7 I [12], GL. IV, x7.
242
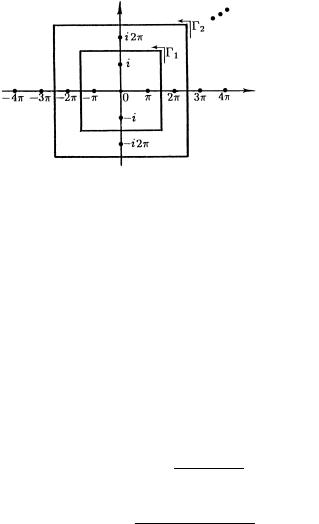
pRIMER. u MEROMORFNOJ FUNKCII w = ctgz POL@SAMI
(1-GO PORQDKA) SLUVAT TO^KI zj = j j = 0 1 2 : : : .
rIS. 83
eSLI ZA POSLEDOWATELXNOSTX |
|
;n |
KONTUROW WZQTX POSLE- |
|||||||||||||||||||||||||||||||||||
DOWATELXNOSTX ODNOKRATNO OBHODIMYH W POLOVITELXNOM NA- |
||||||||||||||||||||||||||||||||||||||
PRAWLENII KWADRATOW |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
;n = z 2 |
C |
: jRezj= n+ 2 |
|
_ jImzj= n+ 2 |
|
|
|
|
( |
RIS |
. 83), |
|||||||||||||||||||||||||||
TO USLOWIQ |
1 I 2 |
BUDyT ZAWEDOMO WYPOLNENY. oSTAETSQ (DLQ |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
PROWERKI WYPOLNENIQ USLOWIQ |
3 ) OCENITX WELI^INU jctgzj |
|||||||||||||||||||||||||||||||||||||
NA STORONAH \TIH KWADRATOW. pOSKOLXKU |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
jctg zj |
2 |
= |
|
cos(x+iy) |
2 |
= |
e;2y +e2y+2 cos 2x |
|
, |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
sin(x+iy) |
|
e;2y+e2y;2 cos 2x |
|
|
|
1 |
|
|
|
|
|
||||||||||||||||||||||||
NA \WERTIKALXNYH" STORONAH, T. E. PRI z = |
|
n+ |
|
+iy, |
||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2y |
|
|
2y |
|
|
|
|
|
|
|
; |
|
|
|
2 |
|
|
|
|
|
|||||
|
|
|
|
|
j |
ctg z |
2 = |
e; |
+e |
;2 |
<1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
2y |
2y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
j |
|
e; |
|
+e |
+2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|||||||||
TOGDA KAK NA \GORIZONTALXNYH", T. E. PRI z =x |
|
|
|
i n+ |
, |
|||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
(2n+1) |
|
|
(2n+1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
ctgz 2 |
6 |
e; +e |
;2 |
|
|
|
|
|
|
1. |
|
|
|
|
|
||||||||||||||||||||
|
|
|
(2n+1) (2n+1) |
n |
+ |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
j |
|
|
j |
|
|
|
e; |
|
|
+e |
|
|
|
+2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
;! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|TO OZNA^AET, ^TO FUNKCIQ w =ctgz |
|
! 1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
OGRANI^ENa NA DAN- |
||||||||||||||||||||||||||||||||||||||
NOJ POSLEDOWATELXNOSTI KONTUROW |
|
;n |
|
I POTOMU (NE OB- |
||||||||||||||||||||||||||||||||||
LADAQ SWOJSTWOM |
3 |
) |
UDOWLETWORQET USLOWI@ |
3 |
|
|
S |
m=1. |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|

243 pEREHOD K FUNKCII w = z;1ctgz, GLAWNYMI ^ASTQMI RQ-
DOW lORANA KOTOROJ W OKRESTNOSTQH TO^EK: z0 = 0 |
|
| ee PO- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
L@SA 2-GO PORQDKA I zj = j |
|
|
j = |
1 2 : : : , | ee POL@SOW |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1-GO PORQDKA) QWLQ@TSQ SOOTWETSTWENNO |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
res ctgz |
|
|
|
res(z;1ctg z) |
|
|
|
|
|
|
|
cos 0 |
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
z=0 |
|
|
|
|
|
|
|
|
|
|
|
z=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
g0(z) = |
|
|
|
z2 |
|
|
+ |
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
= |
|
|
sin0 |
0 z2 |
+ 0 z |
= |
|
z2 |
||||||||||||||||||||||||||||||||||||||||||||||
I |
|
|
|
|
|
res (z;1ctg z) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos j |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
gj(z) = |
|
z= j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
, |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
z; j |
|
|
|
|
|
|
|
(z sin z)z0= j |
|
|
z; j |
|
|
|
j |
|
z; j |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
PRIWODIT K RAZLOVENIQM W OBLASTI C rf0 2 |
: : : g: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
z;1ctg z = |
|
lim |
|
|
|
|
|
|
|
|
|
|
gj(z) = lim |
|
|
|
|
1 |
+ |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
= |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
j z j |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
n |
|
|
+ |
|
|
zj |
|
|
int;n |
|
|
|
|
|
|
|
|
|
|
n |
|
|
+ |
1 |
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
! |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
! |
|
|
|
|
|
|
|
|
n6j6n |
|
|
|
|
|
; |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; j=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+1 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= z2 |
|
+ j=1 j |
z; j ; z+ j |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
+1 |
|
|
|
|
|
2z |
|
|
|
|
|
|
|
|
1 |
|
|
|
+1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
ctg z = |
|
z |
+ |
j=1 |
z2 |
|
|
|
|
( j)2 = z |
+ |
|
|
|
|
|
z |
|
|
|
j + z+ j |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
(\RASKRYTIE SKOBOK" W PRAWYH ^ASTQH OBOIH RAZLOVENIJ NE |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
DOPUSKAETSQ: OBA RQDA |
+1 |
|
|
|
1 |
|
|
|
|
I |
|
|
+1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
PO OTDELXNOSTI |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
z |
|
j |
|
|
|
|
|
|
|
|
|
z+ j |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
RASHODQTSQ!). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
; |
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
zAPISAW POSLEDNEE RAZLOVENIE W WIDE |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
ctgz |
|
1 |
= +1 |
|
|
|
|
1 |
|
|
|
+ |
|
|
|
1 |
|
|
|
|
|
|
, |
|
|
|
|
z |
|
|
|
C |
|
|
z = |
|
|
|
|
|
|
|
2 : : : ,1 |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
; z |
|
|
j=1 z; j |
|
|
|
|
|
z+ j |
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
MOVNO UTWERVDATX, ^TO ESLI TO^KA |
|
|
|
OSTAETSQ W PREDELAH |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
P |
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
T. E. |
jzj |
6 r , TO DLQ L@BOGO |
|||||||||||||||||||||||||||||||||||||||||||||||
KRUGA RADIUSA |
|
S CENTROM |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(SKOLX UGODNO MALOGO) POLOVITELXNOGO ^ISLA |
" |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1 dLQ FUNKCII w = ctg z |
; |
|
|
OSOBAQ TO^KA z = 0 QWLQETSQ USTRA- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
z |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
NIMOJ, A POTOMU ZNA^ENIE |
|
z = 0 |
|
|
OKAZYWAETSQ DLQ \TOJ FUNKCII (PRI |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
DOOPREDELENII ctg z |
|
|
1 |
|
|
|
|
|
def |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
= 0) DOPUSTIMYM. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
; z z=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||

244
|
|
1 |
|
n |
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
ctg z ; z ; j=1 z |
; |
j +z+ j 6 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
+P |
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
1 |
|
|||
|
|
|
P |
|
|
|
1 |
|
|
|
1 |
|
|
|
P |
|
|
|
||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||||||
6 |
|
z |
; |
j + z+ j 6 |
2 |
|
|
j |
; |
r <" |
||||||||||||||
LI[X TOLXKO n |
j=n+1 |
|
|
|
; |
j=n+1 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
DOSTATO^NO WELIKO |
n |
>n0(" r) |
|
. |
||||||||||||||||||||
rIS. 84
s^ITAQ TEPERX, ^TO z | L@BAQ (NO FIKSIROWANNAQ) TO^-
KA OBLASTI C rf 2 : : : g, a L |
| KAKAQ-LIBO LOMANAQ |
|||||||||||||
(DLINY l(L)) S NA^ALXNOJ TO^KOJ 0 I KONE^NOJ z, NE WYHODQ- |
||||||||||||||
]AQ ZA PREDELY \TOJ OBLASTI (RIS. 84), MOVNO UTWERVDATX, |
||||||||||||||
^TO DLQ cKOLX UGODNO MALOGO ^ISLA " > 0 |
I L@BOJ TO^KI |
|||||||||||||
2C c j j6l(L) |
n |
|
|
|
|
|
|
+1 |
|
|
|
|||
ctg z |
|
1 |
|
1 |
|
1 |
|
|
|
1 |
|
|
||
|
|
|
|
|
+ |
|
|
6 |
2 |
|
|
<" |
||
|
; z ; jP=1 z; j z+ j |
j=Pn+1 |
j;l(L) |
|
||||||||||
; |
|
|
||||||||||||
LI[X TOLXKO n |
DOSTATO^NO WELIKO |
|
|
|
|
|
||||||||
|
n >n0(" L) . s U^ETOM |
|||||||||||||
OCENKI INTEGRALA (VIII, c. 133) IZ \TIH NERAWENSTW SLEDUET, ^TO
|
|
|
1 |
n |
|
|
1 |
|
1 |
|
|
|
|
|
P R |
|
|
|
|
||||
1 |
R |
ctg ; |
|
|
|
|
|
< " l(L), |
|||
|
L |
d ; j=1 |
L |
; j + + j d |
|||||||
t. E. RQD DROBEJ W RAZLOVENII KOTANGENSA SHODITSQ RAWNOMERNO
NA KAVDOM OGRANI^ENNOM MNOVESTWE OBLASTI C r 0 2 : : : .

245
A SLEDOWATELXNO, | W SILU WOZMOVNOSTI PEREHODA K PREDELU
PRI " |
! |
0 (WLEKU]EMU STREMLENIE n K + |
1 |
) | |
|
|
||||||||||||
|
|
|
1 |
|
|
|
n |
|
|
1 |
|
1 |
|
|
||||
|
|
|
ctg |
|
|
d = |
lim |
|
|
|
+ |
|
|
d . |
||||
|
|
|
; |
|
|
|
; j |
+ j |
||||||||||
|
L |
|
|
n!+1 j=1 |
L |
|
|
|
||||||||||
|
R |
|
|
|
|
|
|
|
P R |
|
|
|
|
|
|
|
|
|
pRIMENENIE K INTEGRALAM FORMULY nX@TONA{lEJBNICA
(SLU^AJ MNOGOZNA^NOJ PERWOOBRAZNOJ IX, c. 135) I POSLEDU- @]EE POTENCIROWANIE DA@T:
|
|
|
|
1 |
|
|
|
|
|
M |
|
sin |
|
|
|
sin |
|
|
|
|
|
L |
ctg ; |
|
d = |
Ln |
|
L= ln |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
||||||||||||||||
R |
|
1 |
+ |
|
1 |
|
|
d = MLn( |
|
j) L+ MLn( + j) L= |
|
|
|
||||||||
L |
; j |
+ j |
; |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
2 |
|
= ln(z; j) |
; ln(; j) + |
ln(z+ j) ; ln( j) = ln 1; j |
|||||||||||||||||||
(ZNA^ENIQ LOGARIFMOW ZAWISQT OT WYBORA IH ODNOZNA^NYH |
|||||||||||||||||||||
|
; |
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
WETWEJ WDOLX LOMANOJ L, NO IZMENENIQ SWODQTSQ K SLAGAEMYM, KRATNYM 2 i, A POTOMU \IS^EZA@]IM" PRI POTENCI-
ROWANII) |
|
|
z |
|
|
|
|
n!+1j=1 |
|
; j |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
sin z |
|
|
|
|
|
|
|
|
sin z |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
z |
2 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
= exp ln |
|
|
|
|
= exp lim |
|
|
ln 1 |
|
|
|
|
= |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
! 1 P |
|
|
|
|
|
|
|
|
|
|
|
! 1 Q |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
n + |
|
|
|
|
|
|
|
n |
|
|
|
j |
P |
|
n + |
|
|
n |
|
|
j |
|
|
|
||||||||||||||||
|
|
|
|
|
= lim |
exp |
|
|
|
ln 1 |
; |
|
|
|
z |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
z |
2 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
lim |
1 |
; |
|
|
|
|
|
. |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j=1 |
|
|
|
|
|
|
|
|
|||||||
|
wYWOD: IMEET MESTO RAZLOVENIE SINUSA W BESKONE^NOE |
|||||||||||||||||||||||||||||||||||||||||||||
PROIZWEDENIE1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
+1 |
|
|
|
|
z |
2 |
|
|
|
|
|
|
z |
|
|
|
|
|
z |
|
|
|
z |
|
|
|
z |
|
|
|
|
|
|||||||||
|
sin z = zj=1 1; j |
|
|
= z 1; |
1+ |
1; |
2 1+ 2 |
, |
|
|||||||||||||||||||||||||||||||||||||
SLEDSTWIEM KOTOROGO (PRI z = |
|
|
) QWLQETSQ |
FORMULA wALLISA |
|
|||||||||||||||||||||||||||||||||||||||||
2 |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
= 2 2 4 4 6 6 |
|
|
|
= lim |
|
|
|
2 2 4 4 2n 2n |
|
|
|
|
|
. |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
def |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
2 |
|
|
1 3 |
|
3 5 |
|
5 7 |
|
n!+11 3 3 5 5 (2n;1) (2n+1) |
|
|
|
|
|
|||||||||||||||||||||||||||||
1 wYWEDENNOE |JLEROM (IZ DRUGIH SOOBRAVENIJ) W [19], GL. IX.

246
|TA FORMULA BYLA WYWEDENA wALLISOM1 W IZDANNOJ W 1656 G. \aRIF- METIKE BESKONE^NOSTEJ" (\Arithmetica In nitorum") POSREDSTWOM CEPI
PREOBRAZOWANIJ INTEGRALA W RAWENSTWE = R 1p1 ; x2dx. o ROLI \TOGO AWTORA W RAZWITII MATEMATIKI GOWORIT4UVE 0TO, ^TO IMENNO ON
WWEL SIMWOL 1 (I, S. 22) I TERMIN \INTERPOLQCIQ"
NA[EL ZNA^ENIE \LEMENTA (TO^NEE, DIFFERENCIALA) DLINY GLADKOJ
DUGI: dl =p1+(y0(x))2dx
POKAZAL \REALXNOSTX" MNIMYH ^ISEL2 I DAL KL@^ K IH GEOMETRI- ^ESKOJ TRAKTOWKE, PRIWEDQ W SWOEM IZDANNOM W 1685 G. \kURSE aLGEB-
RY" (\Treatise of Algebra") SLEDU@]IE RASSUVDENIQ: \These Imaginary Quantities (as they are commonly called) arising from the supposed root of a negative square (when they happen) are reputed to imply that the case proposed is Impossible . But suppose that we gain from the sea 10 acres, but that we lose 20. Our gain must be ;10 acres, or ;1600 square perches3. Now suppose this negative plain, ;1600 square perches, to be in the form of a square, must not this supposed square be supposed to have a side? And if so, what shall this side be? We cannot say that it is 40 or ;40, but it is p;1600, or 40p;1, where p signi es a mean proportional between a positive and a negative quantity".
|
uPRAVNENIQ. |
1. dOKAZATX, ^TO MEROMORFNAQ FUNKCIQ QWLQETSQ RA- |
|||||||||||||||||||||||||
CIONALXNOJ W TOM I TOLXKO W TOM SLU^AE, KOGDA 1 QWLQETSQ DLQ NEE |
|||||||||||||||||||||||||||
USTRANIMOJ OSOBOJ TO^KOJ ILI POL@SOM. |
|
|
|
|
|
|
|
||||||||||||||||||||
|
2. dOKAZATX, ^TO ESLI DLQ FUNKCII w =f(z) BESKONE^NOSTX QWLQ- |
||||||||||||||||||||||||||
ETSQ a) USTRANIMOJ OSOBOJ TO^KOJ |
|
ILI B) POL@SOM PORQDKA 6k, TO |
|||||||||||||||||||||||||
a) res f(z) = lim |
|
|
z2f0(z) |
B) res f(z) = ( |
1)k |
|
1 |
|
lim zk+2f(k+1)(z) . |
||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||
z= |
1 |
z |
!1 |
|
|
|
|
z= |
1 |
|
|
; |
|
(k+1)! z |
!1 |
||||||||||||
|
3. oPIRAQSX NA; TEOREMU |
wEJER[TRASSA (XI, c. 174),;POLU^ITX DIF- |
|||||||||||||||||||||||||
FERENCIROWANIEM RAZLOVENIQ KOTANGENSA (c. 243) RAZLOVENIE |
|||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
+1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
= |
P |
|
|
2 , z |
2 |
C z =0 |
|
|
|
2 : : : |
||||||||||
|
|
|
|
|
|
j=;1 (z; j) |
|||||||||||||||||||||
|
|
|
sin |
z |
|
|
|
|
|
|
|
|
6 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1 I, SNOSKA 2 NA S. 13. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
2 w PROTIWOWES IH IZOBRETATELQM |
| |
ITALXQNSKIM MATEMATIKAM |
|||||||||||||||||||||||||
XVI W. (I, S. 12), S^ITAW[IM IH \FIKCIEJ".
3 aNGL. perch ([EST) | MERA DLINY (=5,03 M) square perch (KWAD-
RATNYJ [EST) | MERA PLO]ADI (=25,3 M2).

247
XVI. kAK, PRIMENQQ WY^ETY, WY^ISLQ@T INTEGRALY PO NEZAMKNUTYM KONTURAM
iSPOLXZUQ DEMONSTRIRUEMYE NIVE PRIEMY, WY^ISLENIe
KONTURNYH INTEGRALOW S POMO]X@ WY^ETOW MOVNO RASPRO-
STRANITX1 NA INTEGRALY PO NEZAMKNUTYM KONTURAM I PREV- DE WSEGO | PO PROMEVUTKAM DEJSTWITELXNOJ OSI.
sUTX \TIH PRIEMOW SOSTOIT W DOPOLNENII NEZAMKNUTYH KONTUROW DO ZAMKNUTYH S POSLEDU@]EJ OCENKOJ INTEGRALOW PO \ZAMYKA@]IM" GLADKIM DUGAM. sDELATX \TU OCENKU BOLEE EDINOOBRAZNOJ POZWOLQ@T SLEDU@]IE UTWERVDENIQ.
lEMMY OB INTEGRALAH PO DUGAM OKRUVNOSTEJ.2
1. pUSTX FUNKCIQ w =f(z) OBLADAET SWOJSTWAMI:
1) INTEGRAL Rf(z)dz, GDE Cr | DUGa OKRUVNOSTI RA-
Cr
DIUSA r S CENTROM
BOLX[IH (SOOTWETSTWENNO DOSTATO^NO MALYH) r >0
rIS. 85
1 iDEQ \TOGO RASPROSTRANENIQ WOSHODIT K MEMUARU kO[I [27].
2 iMENNO DUGAMI OKRUVNOSTEJ OBY^NO DOPOLNQ@T NEZAMKNUTYE
KONTURY S CELX@ PREOBRAZOWANIQ IH W ZAMKNUTYE.

248
2) z f(z) ! 0 |
PRI z !1 (SOOTWETSTWENNO z !0)1 |
|||||||
TOGDA |
R |
f(z)dz !0 PRI |
r !+1 (SOOTWETSTWENNO r !0)2. |
|||||
|
Cr |
|
|
|
|
|
|
|
2. |
eSLI DLQ ANALITI^ESKOJ FUNKCII w = f(z)TO^KA z0 |
|||||||
QWLQETSQ POL@SOM 1-GO PORQDKA, a GLADKIE DUGI L1 |
I L2 PE- |
|||||||
RESEKA@TSQ W \TOJ TO^KE POD UGLOM (0 6 62 |
RIS. 86), |
|||||||
TO DLQ INTEGRALOW CRrf(z)dz PO ZAKL@^ENNYM MEVDU L1 I L2 |
||||||||
DUGAM |
Cr OKRUVNOSTEJ |
|
z 2 C : |
jz ;z0j = r (OBHODIMYM W |
||||
POLOVITELXNOM NAPRAWLENII), |
SPRAWEDLIWO PREDELXNOE SO- |
|||||||
OTNO[ENIE lim |
R |
f(z)dz = i resf(z). |
|
|||||
|
|
r!0 |
Cr |
|
z=z0 |
|
||
rIS. 86
3 (LEMMA vORDANA).3 pUSTX FUNKCIQ w = f(z) (NE OBQZATELXNO ANALITI^ESKAQ) OBLADAET SWOJSTWAMI:
1 pO KRAJNEJ MERE PO MNOVESTWU, SODERVA]EMU WSE DUGI Cr.
2 nEZAWISIMO OT RASTWORA I NAPRAWLENIQ OBHODA
3 pRIWEDENA WO 2-M TOME \kURSE ANALIZA" (\Cours d'Analyse de
FRANCUZSKOGO MATEMATIKA vORDANA
l'Ecole Polytechnique") (Jordan, Camille, 1838 {1922): W IZDANII 1913 G. NA S. 331.

|
|
|
|
R |
249 |
|
1) DLQ POLOVITELXNOGO ^ISLA INTEGRAL |
f(z)ei zdz |
|||||
|
||||||
|
|
|
|
Cr |
|
|
PO POLUOKRUVNOSTI Cr = |
z 2 C |
: jzj = r ^ 0 |
6 arg z 6 |
|||
(RIS. 87, a) OPREDELEN DLQ DOSTATO^NO BOLX[IH r >0
|
|
|
rIS. 87 |
2) |
lim f(z) = 0 |
||
|
z!1 |
|
|
|
Im z>0 |
R |
|
TOGDA |
lim |
f(z)ei zdz = 0. |
|
|
r!+1 |
Cr |
|
dOKAZATELXSTWa. 1. w SILU WTOROGO IZ USLOWIJ LEMMY
DLQ L@BOGO (SKOLX UGODNO MALOGO) ^ISLA " > 0 SU]ESTWUET |
||||||||||||||||||
NASTOLXKO BOLX[OE (SOOTWETSTWENNO NASTOLXKO MALOE) ^ISLO |
||||||||||||||||||
r" > 0, ^TO |
z |
f(z) |
|
< |
" |
PRI |
jzj > r" (SOOTWETSTWENNO PRI |
|||||||||||
|
2 |
|||||||||||||||||
0 < jzj |
< r"). |
tOGDA SOGLASNO OCENKE INTEGRALA PO KONTURU |
||||||||||||||||
(VIII, c. 133) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
R |
f(z)dz = |
|
R |
z f(z) dz < |
" |
|
1 |
l(Cr) 6 |
" |
2 r = " |
|||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
z |
|
|
2 r |
|
2 r |
|||||||
|
Cr |
|
|
|
Cr |
|
|
|
|
|
|
|
|
|
|
|
||
LI[X TOLXKO r >r" |
|
(SOOTWETSTWENNO 0<r <r"). |
||||||||||||||||
2. |
|
pREDSTAWLENIE TO^EK z |
DUGI Cr |
W WIDE z = z0 + reit, |
||||||||||||||
t2[ r r] (KAK NA RIS. 86) POZWOLQET ZAPISATX:
250
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
f(z)dz = |
|
|
|
f z0 +reit |
|
|
reitidt = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
Cr |
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
R |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
R |
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
= |
|
|
|
f z0 +reit |
reiti |
|
; |
i res f(z) + i res f(z) dt = |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
r |
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z=z0 |
|
|
|
|
|
z=z0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
R r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
= i |
|
|
|
|
f z0 +reit |
|
reit |
|
|
|
res f(z) dt + i r |
|
|
|
|
|
r |
res f(z). |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
Rr |
0 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
;z=z0 |
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
; |
|
|
|
|
z=z0 |
|
1 |
||||||||||||||||||||||||
|
|
|
|
pRI r |
! |
|
WTOROE SLAGAEMOE W PRAWOJ ^ASTI STREMITSQ |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
K i resf(z), PERWOE VE (INTEGRALXNOE) SLAGAEMOE STREMITSQ |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
z=z0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
K NUL@, TAK KAK PO FORMULE WY^ETA FUNKCII W POL@SE 1-GO |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
PORQDKA |
|
res f(z) = |
lim |
|
|
f(z)(z |
; |
z0) (XV, c. 232), A POTOMU |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
z=z0 |
|
|
|
|
|
|
|
z!z0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
" SU]EST- |
||||||||||||||||||
DLQ SKOLX UGODNO MALOGO POLOVITELXNOGO ^ISLA |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
WUET TAKOE (ZAWISQ]EE OT NEGO) POLOVITELXNOE ^ISLO , ^TO |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
f(z)(z |
; |
z0) |
|
res f(z) < |
" |
|
|
|
KAK TOLXKO 0< |
z |
; |
z0 |
j |
< , |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
;z=z0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
||||||||||||||||
I, |
SLEDOWATELXNO, ESLI 0<r < , TO |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
f z0 +reit reit |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
" |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
res f(z) dt < ( r |
; |
r) |
|
|
|
6 |
". |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
Rr ; |
|
|
|
|
|
|
|
|
|
|
|
|
;z=z0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
w SILU WTOROGO IZ USLOWIJ LEMMY DLQ L@BOGO (SKOLX |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
UGODNO MALOGO) ^ISLA " > 0 |
|
SU]ESTWUET NASTOLXKO BOLX[OE |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
^ISLO r" > 0, ^TO |
|
|
f(z) < |
" |
|
|
|
PRI |
|
z > r" Im z > 0. pREDc- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
TAWLENIE VE TO^EK |
|
z |
2 |
|
Cr |
|
W WIDE jzj= reit = r(cos t+i sin t), |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
t2[0 ], |
POZWOLQET ZAPISATX |
|
PRI |
|
|
|
r > r": |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
f(z)ei z dz = |
|
f |
reit |
|
|
ei r(cos t+i sin t) reitidt |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Cr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
it |
|
|
|
r sin t |
|
|
|
|
|
|
|
|
|
|
|
" |
|
|
|
|
r sin t |
|
|
|
|
2 |
" |
|
|
|
|
r sin t |
|
|
||||||||||||||||||||||||||||||
6 |
|
|
|
|
|
f re |
|
|
|
e; |
|
|
|
|
r dt < |
|
|
|
|
|
e; |
|
|
|
|
|
|
|
rdt = 2 |
|
|
|
|
|
e; |
|
|
|
rdt, |
|||||||||||||||||||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
> |
|
2 |
|
|
|
|
|
6 |
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
A SLEDOWATELXNO (TAK KAK sin t |
|
|
|
|
t |
PRI 0 |
t |
6 |
|
|
|
|
|
RIS. 87, B), |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
1 pOSKOLXKU |
|
lim( r |
; |
r) = . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
! |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
