Файловый архив студентов. Файловый архив студентов.
1261 вуз, 4607 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Национальный исследовательский ядерный университет (МИФИ)
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

Шведенко Начала анализа функций комплексной переменной 2008

.pdf
Скачиваний:
84
Добавлен:
16.08.2013
Размер:
51.53 Mб
Скачать
☆

111

sOPOSTAWLENIE POSLEDNEGO UTWERVDENIQ S OPREDELENIEM

ANALITI^NOSKOJ FUNKCII (S. 105) I KRITERIEM SU]ESTWOWA-

NIQ PROIZWODNOJ FUNKCII KOMPLEKSNOJ PEREMENNOJ (V , c. 73,

77)POZWOLQET SDELATX SLEDU@]IE WYWODY.

1.l@BU@ ANALITI^ESKU@ FUNKCI@ MOVNO S^ITATX TA- KOWOJ W NEKOTOROJ OBLASTI.1

2.fUNKCIQ w = f(z) QWLQETSQ ANALITI^ESKOJ W OBLAS-

TI D C W TOM I TOLXKO W TOM SLU^AE, KOGDA ONA IMEET PROIZWODNU@ f0(z) W KAVDOJ TO^KE \TOJ OBLASTI.2

3.dLQ TOGO ^TOBY FUNKCIQ w = f(z) BYLA ANALITI-

^ESKOJ W OBLASTI D C , DOSTATO^NO, ^TOBY KAK FUNKCIQ w =f(x+iy) DWUH DEJSTWITELXNYH PEREMENNYH ONA IMELA W

\TOJ OBLASTI NEPRERYWNYE ^ASTNYe PROIZWODNYe

@f

@f S

 

 

 

 

@f@x +i @f@y = 0

@x

@y

WYPOLNENIEM USLOWIQ kO[I{rIMANA

 

(A W PO-

LQRNYH KOORDINATAH | NEPRERYWNYE ^ASTNYE PROIZWODNYE

@f

@f S WYPOLNENIEM USLOWIQ

@f +

i

@f =0).

 

 

@r

 

 

 

@'

@r

r @'

 

 

 

kAK SLEDSTWIQ, SPRAWEDLIWY SLEDU@]IE UTWERVDENIQ.

P

P

 

+1

+1

cn(z;z0)n | STEPENNOGO

CUMMY RQDOW n=0cn(z;z0)n

I n=

 

I OBOB]ENNOGO STEPENNOGO

 

;1

| QWLQ@TSQ ANALITI^ESKIMI

FUNKCIQMI SOOTWETSTWENNO W KRUGE I KOLXCE SHODIMOSTI

\TIH RQDOW (V , S. 72).

 

 

 

1 eSLI OTKRYTOE (c. 106) MNOVESTWO O WSEH TO^EK ANALITI^NOSTI

FUNKCII w = f(z) NE QWLQETSQ OBLASTX@, TO ONO OKAZYWAETSQ OB_EDI-

NENIEM O = [Dj NEPERESEKA@]IHSQ OBLASTEJ, I FUNKCI@ w = f(z)

j

UDOBNEE IZU^ATX OTDELXNO W KAVDOJ IZ NIH.

2 tOGDA KAK SU]ESTWOWANIE U FUNKCII PROIZWODNOJ W TO^KE I EE ANALITI^NOSTX W TO^KE | \TO RAZNYE TREBOWANIQ (PRIMER FUNKCII w =jzj2 NA S. 107).

112

|KSPONENCIALXNAQ FUNKCIQ w = exp x= ez (II, c. 36) QWLQ- ETSQ ANALITI^ESKOJ WO WSEJ PLOSKOSTI C (T. E. CELOJ).

oDNOZNA^NAQ WETWX LOGARIFMA w = ln z = ln r + i' QWLQ- ETSQ ANALITI^ESKOJ FUNKCIEJ W L@BOJ OBLASTI D C , GDE OPREDELENA ODNOZNA^NAQ WETWX ARGUMENTA ' = arg z (NAPRIMER, W PLOSKOSTI C c \RAZREZOM" PO L@BOMU LU^U,

WYHODQ]EMU IZ TO^KI 0 V, c. 78).

|LEMENTARNYE FUNKCII1 (W SLU^AE IH MNOGOZNA^NOSTI | IH ODNOZNA^NYE WETWI) QWLQ@TSQ ANALITI^ESKIMI W TEH

OBLASTQH PLOSKOSTI C , GDE ONI OPREDELENY.

uSLOWIQ POSTOQNSTWA ANALITI^ESKOJ FUNKCII W OBLASTI. eSLI DLQ FUNKCII w = f(z), ANALITI^ESKOJ W OB-

LASTI D C , WYPOLNENO ODNO IZ USLOWIJ:

1) f0(z) 0 2) Ref(z) c

3) Imf(z) c

4) arg f(z) c 5)

jf(z)jc

(GDE c | NEKOTOROE DEJSTWITELXNOE ^ISLO), TO \TA FUNKCIQ QWLQETSQ POSTOQNNOJ W OBLASTI D.

dOKAZATELXSTWO. kAVDOE IZ \TIH PQTI USLOWIJ WLE^ET

RAWENSTWO NUL@ (W KAVDOJ TO^KE OBLASTI D) ^ASTNYH PRO-

IZWODNYH

@u

 

@u

 

@v

 

@v

FUNKCIJ u = Ref(x + iy) I

 

 

@x

@y

 

@x

@y

 

 

v = Imf(x + iy). w PERWYH TREH SLU^AQH \TO WYTEKAET IZ USLOWIQ kO[I{rIMANA @f@x +i @f@y =0 WKUPE S SOOTNO[ENIQMI

f0(z)= @f

@f =

@u

+i

@v

 

@f

=

@u

 

+i

@v

(V, c. 73).

 

 

@y

@y

 

@x

@x

@x @x

 

 

 

@y

 

~ETWERTYJ SLU^AJ SWODITSQ K TRETXEMU (UMNOVENIEM FUNK-

 

6

;

 

 

 

 

 

 

 

 

CII NA ^ISLO e;ic): Im e;icf(z) =0. w PQTOM SLU^AE f(z)

0,

ESLI c= 0, a ESLI c = 0, TO TOVDESTWO u2(x y) + v2(x y)

c2

WLE^ET WYPOLNENIE W KAVDOJ TO^KE (x y)2D RAWENSTW

1 T. E. WYRAVAEMYE ^EREZ PEREMENNU@ I KONSTANTY KOMBINACIQMI

^ETYREH OSNOWNYH DEJSTWIJ, \KSPONENTY I LOGARIFMA (III, c. 51).

f(z)=60
PRINIMAET RAWNYE ZNA^ENIQ. Q.E.D.

113

(@u@x u+ @x@v v =0 @u@y u+ @v@y v =0:

rASSMATRIWAQ \TI RAWENSTWA KAK ODNORODNU@ SISTEMU LI-

NEJNYH ALGEBRAI^ESKIH URAWNENIJ, IME@]U@ NENULEWOE RE-

[ENIE (u v), MOVNO UTWERVDATX, ^TO OPREDELITELX \TOJ SISTEMY RAWEN NUL@ W L@BOJ TO^KE (x y)2D, A SLEDOWATELX-

NO (c U^ETOM USLOWIJ kO[I{rIMANA), RAWNY NUL@ W OBLASTI

D WSE ^ASTNYE PROIZWODNYE @u@x @u@y @x@v @y@v .

dLQ ZAWER[ENIQ DOKAZATELXSTWA OSTAETSQ WOSPOLXZOWATX- SQ SWOJSTWOM SOEDINIMOSTI TO^EK OBLASTI POSREDSTWOM LOMANYH (S. 107): KAKOWY BY NI BYLI TO^KI z0 z1 2D, SU]EST- WUET SOEDINQ@]AQ IH LOMANAQ L D, KAVDYJ IZ SOSTAWLQ- @]IH OTREZKOW KOTOROJ PARALLELEN ODNOJ IZ OSEJ KOORDINAT (KAK NA RIS. 33, B). nA KAVDOM IZ \TIH OTREZKOW ZNA^ENIQ u(x y) I v(x y) QWLQ@TSQ FUNKCIQMI TOLXKO ODNOJ PERE- MENNOJ (x ILI y), PROIZWODNAQ PO KOTOROJ RAWNA NUL@ NA \TOM OTREZKE. wYWOD: FUNKCII u = u(x y) I v = v(x y) QW- LQ@TSQ POSTOQNNYMI NA KAVDOM OTREZKE LOMANOJ, A SLEDO- WATELXNO, f(z0)=f(z1), T. E. FUNKCIQ w =f(z) W L@BYH DWUH TO^KAH OBLASTI D

wOT PRQMOE SLEDSTWIE DOKAZANNYH USLOWIJ POSTOQNSTWA.

wOSSTANOWLENIE ANALITI^ESKOJ FUNKCII PO EE DEJSTWITELX- NOJ (MNIMOJ) ^ASTI ILI MODUL@ (ARGUMENTU)

1

D

 

 

FUNKCIQ w = f(z) WOS-

ANALITI^ESKAQ W OBLASTI

 

C

STANAWLIWAETSQ : a) S TO^NOSTX@ DO POSTOQNNOGO SLAGAE-

MOGO PO SWOEJ DEJSTWITELXNOJ (ILI MNIMOJ) ^ASTI B) S TO^NOSTX@ DO POSTOQNNOGO MNOVITELQ PO SWOEMU MODUL@

(ILI ARGUMENTU, ESLI W OBLASTI D).

1 pO KRAJNEJ MERE W PRINCIPE.

114

tRADICIONNYJ SPOSOB PRAKTI^ESKOGO WOSSTANOWLENIQ ANALITI^ESKOJ FUNKCII w = f(z), NAPRIMER, PO EE DEJSTWITELXNOJ ^ASTI u=u(x y) SOSTOIT W

1)

RE[ENII | OTNOSITELXNO

v = v(x y) PRI ZADANNOJ

FUNKCII u = u(x y) | SISTEMY URAWNENIJ kO[I{rIMANA

(

@u

=

@v

 

 

 

 

@x

 

@y

(PRI \TOM FUNKCIQ

v = v(x y) OPREDELQETSQ S

@u

=;

@v

 

 

 

 

@y

@x

 

 

TO^NOSTX@ DO POSTOQNNOGO SLAGAEMOGO) I

2)

 

POSLEDU@]EJ ZAPISI FUNKCII w = u(x y) + iv(x y)

W WIDE w = f(z) (KAK FUNKCII NE DWUH DEJSTWITELXNYH, A ODNOJ KOMPLEKSNOJ PEREMENNOJ z = x+iy).

tO, ^TO WTOROJ IZ \TIH PUNKTOW INOGDA TREBUET BOLX[IH USILIJ, ^EM PERWYJ, WIDNO IZ PRIMERA u=;2x4 ; 4x3y + 12x2y2 + 4xy3 ; 2y4 : POLU^ITX PREDWARITELXNYJ OTWET

w=;2x4;4x3y + 12x2y2+ 4xy3; 2y4 + i(x4;8x3y ; 6x2y2+ 8xy3+ y4+c)

PRO]E, ^EM OKON^ATELXNYJ w=(i;2)z4 +ic.

bOLEE IZQ]NYJ SPOSOB WOSSTANOWLENIQ ANALITI^ESKOJ FUNKCII PO EE DEJSTWITELXNOJ ^ASTI OPISYWAETSQ SLEDU- @]IM UTWERVDENIEM.

 

 

 

eSLI DEJSTWITELXNAQ ^ASTX u = u(x y) ANALITI^ESKOJ W

 

 

 

OBLASTI D

 

C

 

FUNKCII

w = f(z) DOPUSKAET PODSTANOW-

 

 

 

 

 

z

 

 

 

 

z

 

 

 

 

 

 

 

 

 

 

 

 

z

 

 

 

z

 

 

 

 

 

 

 

 

 

 

 

KU x =

2

 

, y =

2i

(T. E. ZNA^ENIe

u

2

,

2i

 

 

OPREDELENO DLQ

 

 

 

WSEH z

 

D , TO S TO^NOSTX@ DO POSTOQNNOGO SLAGAEMOGO

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

z

 

 

z

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

f(z)=2u

 

 

,

 

 

W OBLASTI D.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

;2

2i

 

 

 

 

 

 

 

 

 

 

 

def

 

 

 

 

z

 

 

z

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dOKAZATELXSTWO.

 

pUSTX f(z) = 2u

 

 

2

,

2i

 

 

 

, GDE z = x+iy.

 

 

 

 

 

 

 

 

 

 

 

tOGDA (WWIDU WYPOLNENIQ DLQ FUNKCII

 

 

w = f(z) USLOWIJ

kO[I{rIMANA)

 

 

 

 

 

 

 

 

 

 

 

e

 

 

;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

@@xf

= 2

;

@u

 

 

1

+

@u

 

1

 

=

@u

;i

@u

=

@u

+i

@v

,

 

 

 

 

@x

2

@y

2i

@x

@y

@x

@x

 

 

 

 

e

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

115

 

 

 

@f = 2

;

@u

 

 

i

+

@u

 

i

 

 

= i

@u

 

+

@u

 

= i

@u

 

;

@v

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

e

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

@y

 

 

 

 

@x

 

 

2

 

 

 

@y

 

 

2i

 

 

 

 

 

 

 

 

@x

 

 

@y

 

 

 

 

 

 

 

@x

 

 

 

 

@x

 

 

e

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

e

 

 

 

 

 

 

 

 

e

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

oTS@DA SLEDUET, ^TO

 

@x@f + i @x@f 0,

A PO\TOMU w =f(z) ESTX

ANALITI^ESKAQ FUNKCIQ W OBLASTI D c PROIZWODNOJ

 

 

 

 

 

 

 

 

 

f0(z)=

@@xf

=

 

 

@u

+ i

@v

 

 

 

x =

z

 

 

= f0

 

z

 

+i

z

 

 

 

=f0(z)

 

 

 

 

 

 

 

 

 

 

 

@x

@x

 

 

2

2i

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

e

 

 

 

 

 

 

e

 

;

 

 

 

 

 

 

 

 

 

 

 

 

 

y=

z

 

 

;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2i

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

z

 

 

 

 

z

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

TAK KAK

 

 

 

 

 

 

e

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

f(z);2u

;

2 , 2i

 

c

 

 

f(z);f(z) 0 0, SLEDUET WYWOD:

 

 

 

 

W OBLASTI D. Q.E.D.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

zAME^ANIE.

 

tAK KAK Imf(z) = Re

;if(z) , FORMULA WOS-

 

 

 

 

STANOWLENIQ ANALITI^ESKOJ FUNKCII w = f(z) PO EE MNIMOJ

^ASTI v=v(x y) IMEET WID

 

 

 

f(z)= 2iv;

z

,

z

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

2i

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

pRIMERY.

1.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4

 

KOGDA

 

 

w RAZOBRANNOM WY[E SLU^AE f(z) = (i;

2)z ,

 

u=;2x4

;

4x3y +12x2y2 +4xy3 ;2y4, PODSTANOWKA x=

z

, y=

z

 

DAET:

2

2i

 

 

;

z

 

z

;

 

 

z4

 

 

2

 

 

z4

 

 

 

2i

 

 

 

z4

 

 

 

 

z4

 

 

 

 

x +y

 

 

 

 

 

 

 

z

 

 

 

 

 

 

 

 

 

2u

 

 

,2i

 

=2 ;2

16 ;4 16i +12 ;16 +4;16i ;2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4

 

 

 

 

 

 

 

2

 

16

 

 

 

 

= (i;2)z .

 

 

 

 

 

pODSTANOWKU

 

 

 

 

 

z

 

 

 

 

 

 

 

 

z

 

 

 

FUNKCIQ

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

;

 

 

 

 

 

1

 

NE DO

 

2.

x =

 

, y =

 

 

 

 

 

u =

2

 

 

 

 

2 = Re

 

 

 

 

-

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

PUSKAET (ZNAMENATELX OBRA]AETSQ W NULX). OBOJTI \TO ZATRUDNENIE POZWOLQET PERENOS NA^ALA KOORDINAT (NAPRIMER, W TO^KU z = 1) | ZA-

MENA z = z

 

1, ILI

x =x

;

1 y = y, PRI KOTOROJ u =

 

x

 

 

=

 

x;21

2

,

 

2

2

 

 

e

 

 

 

 

 

 

 

e

 

 

 

e

 

 

 

 

 

 

 

x +y

 

 

(x

 

1) +y

 

 

;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

;

TAK ^TO

 

2u

;

z

,

z

 

=

 

 

(z=2)

;1

2

=

z;2

=

z;1

=

1

 

 

1. e e

e

 

 

 

 

e

2

 

 

 

 

 

 

e

 

e

 

 

e

e

 

 

 

e

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

2i

 

 

((z=2)

;

1) +(z=2i)

 

 

;

z+1

;

z

z

;

 

 

 

 

 

 

fUNKCI@ u=u(x y) DWUH DEJSTWITELXNYH PEREMENNYH NAZYWA@T

GARMONI^ESKOJ

W oBLASTI D R2, ESLI W \TOJ OBLASTI ONA IMEET NEPRE-

RYWNYE ^ASTNYE PROIZWODNYE 2-GO PORQDKA I UDOWLETWORQET URAWNENI@

lAPLASA1

@2u

+

@2u

=0.

 

 

 

 

 

 

 

 

 

 

 

 

@x2

@y2

;

 

 

 

 

 

 

 

 

 

 

 

 

@

;

 

;

 

@

 

@u

 

 

 

 

 

w ZAPISI

 

@x

 

@x

=

@y

;

@y

 

\TO URAWNENIE WYRAVAET IZWESTNYJ

KRITERIJ TOGO, ^TO

 

 

@u

dx+

@u

dy ESTX DIFFERENCIAL dv=

@v

dx+

@v

dy

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

@y

 

@x

 

 

@x

@y

1 fRANCUZSKIJ MATEMATIK, MEHANIK I ASTRONOM lAPLAS (Laplace, Pierre Simon, 1749 {1827) OPERIROWAL \TIM URAWNENIEM W SWOIH RABO- TAH PO NEBESNOJ MEHANIKE.

tAK KAK W \TOM SLU^AE

116

NEKOTOROJ FUNKCII v =v(x y) (ESLI NE WO WSEJ OBLASTI D, TO PO KRAJ- NEJ MERE W OKRESTNOSTI KAVDOJ EE TO^KI).

@u@x = @v@y , a @u@y = ;@x@v , FUNKCIQ v = v(x y)

TAKVE OKAZYWAETSQ GARMONI^ESKOJ (A FUNKCIQ w = u(x y) + iv(x y) | ANALITI^ESKOJ) PO KRAJNEJ MERE W OKRESTNOSTI KAVDOJ TO^KI OBLAS- TI D.1 w SWQZI S \TIM FUNKCI@ v = v(x y) NAZYWA@T SOPRQVENNOJ GARMONI^ESKOJ PO OTNO[ENI@ K GARMONI^ESKOJ FUNKCII u = u(x y), A

FORMULA

 

v =2Imu

z

 

z

 

 

POZWOLQET EE NAJTI (S TO^NOSTX@ DO POSTO-

 

 

 

 

 

 

 

QNNOGO

 

SLAGAEMOGO);.2

2i

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

uPRAVNENIQ.

1. oB_QSNITX, PO^EMU w=Re z+i Imz | ANALITI^ES-

KAQ FUNKCIQ, A w =(Rez)2+i(Imz)2 | NET.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2. nAJTI WSE ANALITI^ESKIE FUNKCII w = f(z), DEJSTWITELXNAQ

I MNIMAQ ^ASTI KOTORYH u = u(x y) I v = v(x y)

SWQZANY LINEJNYM

SOOTNO[ENIEM au+bv =c

 

(c POSTOQNNYMI a b c).

 

 

 

 

 

 

 

 

 

 

 

3. pROWERITX, ^TO GRAFIK FUNKCII y = sin

1

,

 

x 2 R

x

6= 0, DO-

 

x

 

POLNENNYJ OTREZKOM [

;

1 1] OSI y, QWLQETSQ SWQZNYM, NO NE

LINEJNO

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

.

 

 

 

 

 

 

 

SWQZNYM MNOVESTWOM NA KOORDINATNOJ PLOSKOSTI R

 

 

 

 

 

 

 

 

 

4. wOSSTANOWITX ANALITI^ESKU@ FUNKCI@ w = f(z) PO EE MNIMOJ

 

 

 

 

sh2y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

^ASTI v =

 

.

 

(oTWET: f(z)=tgz.)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

cos 2x+ch 2y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5. wYWESTI FORMULU WOSSTANOWLENIQ f(z) = c exp 2i'

 

z

,

z

 

 

ANA-

 

 

2

2i

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

LITI^ESKOJ FUNKCII w = f(z) PO EE ARGUMENTU ' = '(x y), z = x+iy.

pROWERITX EE NA PRIMERE

arg f(z)=x2 +2xy

;

y2.

 

;

;

 

 

 

 

 

 

6. pROWERIW, ^TO u=ln(x2 + y2+ 2x + 1) | GARMONI^ESKAQ FUNKCIQ W OBLASTI R2 r (;1 0) , NAJTI DLQ NEE SOPRQVENNU@ GARMONI^ESKU@

FUNKCI@ I UBEDITXSQ, ^TO ONA MNOGOZNA^Na W UKAZANNOJ OBLASTI.

1 wO WSEJ OBLASTI D FUNKCII v = v(x y) I w = u(x y) + iv(x y) MOGUT OKAZATXSQ MNOGOZNA^NYMI.

117

VIII. kAK WWODITSQ INTEGRAL PO KOMPLEKSNOJ PEREMENNOJ

iNTEGRAL FUNKCII KOMPLEKSNOJ PEREMENNOJ PO PRIRODE QWLQETSQ KONTURNYM, I POTOMU DATX EGO WNQTNOE OPREDELE- NIE MOVNO, LI[X PRIDAW ^ETKIJ SMYSL PONQTIQM KONTURA

(KUSO^NO-GLADKOGO) NA PLOSKOSTI C I PUTI EGO OBHODA. nA-

^ATX PRI \TOM SLEDUET S PONQTIQ GLADKOJ DUGI.

gLADKAQ DUGA L C | \TO OBRAZ NEKOTOROGO OTREZKA

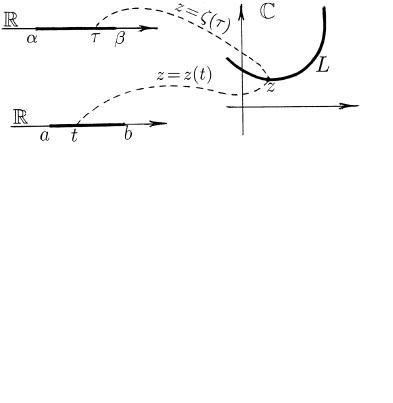
[a b] R PRI WZAIMNO-ODNOZNA^NOM OTOBRAVENII EGO W PLOS- KOSTX C KOMPLEKSNOZNA^NOJ FUNKCIEJ z = z(t) = x(t)+iy(t) (RIS. 35), IME@]EJ NA \TOM OTREZKE NEPRERYWNU@ I NE RAWNU@ NUL@ PROIZWODNU@.1 zNA^ENIQ z(a) z(b) NAZYWA@T PRI \TOM KONCEWYMI, A z(t) a < t < b, | WNUTRENNIMI TO^KAMI

 

 

def

b

 

b

 

 

 

jz0(t)jdt =

(x0(t))2 +(y0(t))2 dt

GLADKOJ DUGI L. ~IcLO l(L) =

 

 

 

 

a

 

a

WYRAVAET

DLINU

\TOJ GLADKOJRDUGI2

Rp

 

rIS. 35

1 w \TOM SLU^AE GOWORQT, ^TO FUNKCIQ z = z(t) a 6 t 6 b, ZADAET

PARAMETRIZACI@

GLADKOJ DUGI L. nA DEJSTWITELXNOJ PLOSKOSTI R2

 

 

(

 

\TA VE GLADKAQ DUGA IMEET PARAMETRIZACI@

x=x(t)

a 6 t 6 b.

 

 

y =y(t)

 

2 sOGLASNO OPREDELENI@ IZ KURSA DEJSTWITELXNOGO ANALIZA.

z(et)6=z0 .

118

nAGLQDNO, GLADKAQ DUGA | \TO PRQMOLINEJNYJ OTREZOK, PODWERG-

NUTYJ OBRATIMOJ GLADKOJ DEFORMACII | RASTQVENI@ I IZGIBU BEZ

RAZRYWOW, IZLOMOW I SKLEIWANIJ. mATEMATI^ESKIM WYRAVENIEM TAKO- GO SRAWNENIQ QWLQ@TSQ SLEDU@]IE UTWERVDENIQ.

1. fUNKCIQ z = z(t) t 2 [a b], ZADA@]AQ PARAMETRIZACI@ GLADKOJ DUGI L, IMEET NEPRERYWNU@ OBRATNU@: t =t(z) z 2L, OBLADA@]U@

NEPRERYWNOJ PROIZWODNOJ t0(z).1

2. w KAVDOJ TO^KE z 2L GLADKAQ DUGA L IMEET KASATELXNU@ PRQMU@ L, NAPRAWLQ@]IJ WEKTOR KOTOROJ QWLQETSQ NEPRERYWNOJ FUNKCIEJ TO^KI KASANIQ.

dOKAZATELXSTWa. 1. sU]ESTWOWANIE FUNKCII t = t(z) z 2 L, ESTX SLEDSTWIE WZAIMNO-oDNOZNA^NOSTI OTOBRAVENIQ z = z(t) t 2[a b]: RAZ-

NYM TO^KAM t2[a b] SOOTWETSTWU@T RAZNYE TO^KI z 2L.

fUNKCIQ t=t(z) z 2L, NEPRERYWNA: DLQ L@BOJ POSLEDOWATELXNOS-

TI fzng TO^EK zn 2 L, SHODQ]EJSQ K TO^KE z0 2 L, SOOTWETSTWU@]AQ

POSLEDOWATELXNOSTX ftng TO^EK tn =t (zn) SHODITSQ K TO^KE t0 =t(z0). eSLI BY \TO BYLO NE TAK, TO U POSLEDOWATELXNOSTI ftng SU]ESTWO-

WALA BY PODPOSLEDOWATELXNOSTX ftnkg, SHODQ]AQSQ K NEKOTOROJ TO^KE et2[a b], OTLI^NOJ OT t0 . tEM SAMYM WOZNIKALO BY PROTIWORE^IE: OD- NOWREMENNO fznkg ! z0 I fznkg=fz(tnk)g !

rIS. 36

1 wELI^INY jz0(t)j I jt0(z)j IME@T SMYSL KO\FFICIENTOW RASTQVE-

NIQ (W TO^KAH t 2 [a b] I z 2 L) PRI DEFORMACII OTREZKA [a b] W

GLADKU@ DUGU L I OBRATNO.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

119

t0(z)= lim

Mt

= lim

 

 

Mz

;1= z0(t) ;1 | S U^ETOM TOGO, ^TO z0(t)=0,

 

 

 

Mt

 

 

 

 

Mz!0 Mz

 

 

Mt!0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

6

A Mz

!

0

()

Mt

!

0

(NEPRERYWNOSTX FUNKCII t=t(z) I z =z(t)).

 

 

 

 

 

 

 

 

 

;

 

 

 

;

 

 

 

 

 

 

 

 

 

 

 

W NAPRAWLENII

2.

pRQMAQ

L,

PROHODQ]AQ ^EREZ TO^KU z0 = z(t0)

NENULEWOGO WEKTORA z0(t0), QWLQETSQ

KASATELXNOJ

K GLADKOJ DUGE L W

TO^KE z0 : ESLI (z L) | RASSTOQNIE OT TO^KI z 2L DO PRQMOJ L, TO

RIS

 

 

 

lim

(z L)

= 0,

TAK KAK PRI

t

 

 

t0

KOGDA

z

 

 

z0

 

 

 

( . 36)

 

 

 

 

 

 

 

 

 

 

 

!

;o(t;t0)

!

0

 

 

 

 

 

 

z!z0 jz;z0j

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

z2L

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(z L)

6 jz(t);z(t0);z

(t0)(t;t0)j

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

jz;z0j

 

 

 

 

 

 

jz(t);z(t0)j

 

 

 

= jz(t);z(t0)j

 

! jz (t0)j.

 

wWIDU NEPRERYWNOSTI ZAWISIMOSTI z0(t) OT t

2

[a b], A t OT z 2 L

(P. 1), NAPRAWLQ@]IJ WEKTOR z0(t(z0)) KASATELXNOJ PRQMOJ L OKAZY-

WAETSQ NEPRERYWNOJ FUNKCIEJ TO^KI KASANIQ z0

2L.

 

Q.E.D.

 

wOT NEKOTORYE PRIMERY GLADKIH DUG L C

 

(WMESTE S IH

PARAMETRIZACIQMI):

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1) OTREZOK PRQMOJ,

SOEDINQ@]IJ TO^KI z0 z1 2C :

 

 

z =z0 +(z1

;z0)t

 

 

 

ILI

z =z1

+(z0

;z1)t , t

2 [0 1]

 

 

 

 

 

 

 

 

2) GRAFIK FUNKCII

y = f(x)

 

 

(ILI x = f(y)), IME@]EJ

 

 

 

 

 

 

 

 

 

 

 

 

 

;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

NEPRERYWNU@ PROIZWODNU@ NA OTREZKE [a b] R :

 

z =x+if(x)

x2[a b],

 

(ILI z =f(y)+iy y 2[a b] RIS. 37)

 

 

rIS. 37

 

 

3) DUGA OKRUVNOSTI

fz 2 C :

jz ;z0j = rg

MEVDU DWUMQ

LU^AMI, WYHODQ]IMI IZ TO^KI z0

POD UGLAMI

I K DEJ-

 

(0 <

 

 

it

STWITELXNOJ OSI

; < 2 ): z = z0 + re t 2 [ ].

 

 

 

 

120

pONQTIQ KONCEWOJ I WNUTRENNEJ TO^EK GLADKOJ DUGI L

I ZNA^ENIE EE DLINY l(L) (S. 117) NE ZAWISQT OT WYBORA

PARAMETRIZACII \TOJ GLADKOJ DUGI, T. E. PRISU]I SAMOJ \TOJ GLADKOJ DUGE.

dOKAZATELXSTWO. eSLI z = z(t) t 2 [a b], I z = ( ) 2 [ ], |

DWe PaRaMETRIZACII (ODNOJ I TOJ VE) GLADKOJ DUGI L, TO KOMPOZICIQ

FUNKCIJ z = ( ) I t = t(z) (OBRATNOJ K z = z(t) S. 118, UTWERVDENIE

1) PRIWODIT K FUNKCII t = t( ( )) S PROIZWODNOJ t0 = t0z 0 = (zt0);1 0 ,

NE RAWNOJ NUL@, A SLEDOWATELXNO, SOHRANQ@]EJ ZNAK NA OTREZKE [ ].

sOOTWETSTWIE $ t 2[ ] t2[a b] (RIS. 38) OKAZYWAETSQ PO\TOMU

STROGO MONOTONNYM, TAK ^TO WNUTRENNIM I KONCEWYM TO^KAM OTREZKA

[ ] OTWE^A@T, SOOTWETSTWENNO, WNUTRENNIE I KONCEWYE TO^KI OTREZ-

KA [a b], PRI \TOM LIBO ( ) = z(a), A ( ) = z(b) (ESLI t0( ) > 0), LIBO

( )=z(b), A ( )=z(a) (ESLI t0( )<0).

 

 

 

 

 

 

 

rIS. 38

 

 

 

 

 

 

 

~TO KASAETSQ FORMULY DLINY l(L) GLADKOJ DUGI, TO W PERWOM SLU-

^AE (PRI t0( )> 0)

 

 

 

 

 

 

 

 

 

 

 

 

b

 

 

 

 

 

 

 

 

 

 

 

 

 

R

 

 

R

 

 

 

R

 

 

 

 

 

 

R

 

 

a jz0(t)jdt =

 

z0(t( )) t0( )d =

 

 

z0(t( )) t0( ) d =

j 0( )jd ,

A WO WTOROM (KOGDA t0( )> 0)

 

 

 

 

 

 

 

 

 

 

b

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

R

jz0(t)jdt =

R

z0

(t( )) t0( )d =;

R

z0(t( )) t0( ) d =

R

j 0( )jd .

Q.E.D.

 

 

 

 

a

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

pOD

SOEDINENIEM

DWUH GLADKIH

DUG

L1 L2 PONIMAETSQ

 

 

NALI^IE U NIH OB]EJ KONCEWOJ TO^KI SOEDINENIE S^ITAETSQ

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности