Добавил:

fench Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский ядерный университет (МИФИ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Шведенко Начала анализа функций комплексной переменной 2008

.pdf

Скачиваний:

Добавлен:

16.08.2013

Размер:

51.53 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 3610 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

kAKOWY BY NI BYLI TRI (RAZNYE) TO^KI z1 z2 z3 2 C I TRI (RAZNYE) TO^KI w1 w2 w3 2 C , SU]ESTWUET I PRI- TOM EDINSTWENNAQ DROBNO-LINEJNAQ FUNKCIQ, PEREWODQ- ]AQ TO^KI z1 z2 z3 SOOTWETSTWENNO W w1 w2 w3.

dOKAZATELXSTWO. eDINSTWENNOSTX TAKOJ FUNKCII WY-

TEKAET IZ TOGO, ^TO ESLI w =w(z) I w=w(z) | DWE DROBNOLINEJNYE FUNKCII, PEREWODQ]IE TO^KI z1 z2 z3 SOOTWET-

STWENNO W w1 w2 w3, A z = w;1(w) \| DROBNO-LINEJNAQ FUNK-
	1				1	e	e	e	;
CIQ,						e		e	w(z) OKA-
CIQ,			OBRATNAQ K w =w(z), TO KOMPOZICIQez =w;1						w(z) OKA-
ZYWAETSQ DROBNO-LINEJNOJ FUNKCIEJ S TEM SWOJSTWOM, ^TO
	;						1
w;		w(zj) = w;				(wj) = zj j = 1 2 3,				-
e				e				I PO\TOMU IME@

]EJ NE MENEE TREH NEPODWIVNYH TO^EK. sOGLASNO PREDY-

		;	;	e
DU]EMU UTWERVDENI@ w; w(z)					z, IZ ^EGO SLEDUET, ^TO
w(z) w w;1 w(z)				w(z).;
e	e		e
	sU]ESTWOWANIE TAKOJ FUNKCII MOVNO WYWESTI ISHODQ

IZ SLEDU@]EGO SOOTNO[ENIQ MEVDU PEREMENNYMI w I z :

w;w1 w3;w2 = z;z1 z3;z2 .1 w;w2 w3;w1 z;z2 z3;z1

dLQ PROWERKI TOGO, ^TO ZAPISANNOE SOOTNO[ENIE DEJST-

WITELXNO OPREDELQET DROBNO-LINEJNU@ FUNKCI@ w = w(z),
DOSTATO^NO WWESTI WSPOMOGATELXNYE DROBNO-LINEJNYE FUNK-
CII =	z;z1	z3	;z2	I	! =	w;w1	w3	;w2	, ^EREZ KOTORYE ZA-
		z3					w3
	z;z2		;z1			w;w2		;w1
WISIMOSTX PEREMENNOJ					w OT PEREMENNOJ z WYRAVAETSQ KAK

w = !;1 (z). tO, ^TO ZNA^ENIQM z = z1 z2 z3 DEJSTWITELXNO SOOTWETSTWU@T ZNA^ENIQ w = w1 w2 w3, PROWERQETSQ PRQMOJ

PODSTANOWKOJ.

Q.E.D.

1 eSLI ODNA IZ TO^EK

z1 z2

ILI

ESTX

TO SOOT-

( ) w1 w2 w3

NO[ENIE PONIMAETSQ KAK EGO PREDEL PRI STREMLENII \TIH TO^EK (\TOJ

TO^KI) K

1, ^TO RAWNOSILXNO ZAMENE NA 1 WSEH SODERVA]IH IH (ee)

^ISLITELEJ I ZNAMENATELEJ:

w;w1

;w2

z3;z2

ESLI (K PRIMERU) z1 =

w;w2

;w1

z;z2

ww;ww21

zz3;zz11

ESLI z2 =1 I w3 =1.

;

zAME^ANIE.

eSLI TO^KI z3 I w3 S^ITATX NEOPREDELENNY-

MI, TO NEOPREDELENNYMI OKAZYWA@TSQ ^ISLA

z3;z2

;w2

z3;z1

;w1

I IZ DOKAZANNOGO UTWERVDENIQ WYTEKAET SLEDU@]EE.

w;w1

z;z1

( | L@BOE NENULEWOE KOMPLEKSNOE ^ISLO)

w;w2

z;z2

ESTX OB]IJ WID TEH DROBNO-LINEJNYH FUNKCIJ, KOTORYE

PEREWODQT TO^KI z1 z2 SOOTWETSTWENNO W TO^KI w1 w2.1

OTOBRAVA@]Ie SWOJSTWA DROBNO-LINEJNYH FUNKCIJ

sWOJSTWO KONFORMNOSTI. oTOBRAVENIE DROBNO-LI-

NEJNOJ FUNKCIEJ w = azcz++db QWLQETSQ KONFORMNYM (W ^AST-

NOSTI, SOHRANQ@]IM UGLY) WO WSEH NEOSOBYH ;z =6 ; dc TO^-

KAH z 2C .

dOKAZATELXSTWO. fUNKCIQ w = azcz++db PRI z 6= ; dc IMEET

az+b 0 ad;bc

PROIZWODNU@ ;cz+d = (cz+d)2 , NE RAWNU@ NUL@, A POTOMU

OTOBRAVENIE \TOJ FUNKCIEJ W L@BOJ TO^KE z 2 C z =6 ;dc ,

QWLQETSQ KONFORMNYM (V, c. 81). Q.E.D.

pRI IZOBRAVENII PEREMENNYH NA SFERE rIMANA (I, S. 21) SWOJST-

WO KONFORMNOSTI OTOBRAVENIJ DROBNO-LINEJNYMI FUNKCIQMI RASPRO-

STRANQETSQ I NA IH \OSOBYE" TO^KI (WKL@^AQ BESKONE^NO UDALENNU@).

sWOJSTWO SOHRANENIQ UGLOW PRI STEREOGRAFI^ESKOJ PROEKCII WYWO-

DITSQ LIBO ANALITI^ESKI (U a. i. mARKU[EWI^A [12] I l. fORDA [18]), LIBO GEOMETRI^ESKI (U d. gILXBERTA I s. kON-fOSSENA [3]).

\kRUGOWOE" SWOJSTWO. oTOBRAVENIE DROBNO-LINEJNOJ

FUNKCIEJ w = azcz++db PREOBRAZUET OKRUVNOSTI I PRQMYE W

OKRUVNOSTI ILI PRQMYE. tO^NEE: OKRUVNOSTI I PRQMYE,

NE PROHODQ]IE ^EREZ \OSOBU@" TO^KU z = d , PREOBRAZU@TSQ

WOKRUVNOSTI, A PROHODQ]IE ^EREZ NEE |cW PRQMYE2.

1 eSLI ODNA IZ TO^EK z1 z2 I/ILI w1 w2 ESTX 1, TO SOOTWETSTWU-

@]IE ^ISLITELI I ZNAMENATELI ZAMENQ@TSQ NA 1.

2 kAVDAQ PRQMAQ S^ITAETSQ PROHODQ]EJ ^EREZ TO^KU 1.0

93 dOKAZATELXSTWO. dELENIE (S OSTATKOM) PRIWODIT DROBNO-

LINEJNU@ FUNKCI@ w =

az+b

K WIDU w =

z +

(PRI c=0)

cz+d

ILI w =

(PRI c=0), T. E. LIBO K LINEJNOJ FUNKCII,

cz+d

LIBO K KOMPOZICII:

LINEJNOJ FUNKCII = cz+d (PEREWODQ]EJ \OSOBU@"

TO^KU z0 =;

W NA^ALO KOORDINAT),

FUNKCII ! =

(S \OSOBOJ" TO^KOJ 0),

LINEJNOJ FUNKCII w = b;

! +

uSTANOWIW \KRUGOWOE" SWOJSTWO; DLQ WSEH

LINEJNYH FUNKCIJ

w = az +b

(S a 6= 0) I FUNKCII w =

, MOVNO S^ITATX EGO

DOKAZANNYM DLQ WSEH DROBNO-LINEJNYH FUNKCIJ.

oTOBRAVENIE w = az+b

z 2C , PREDSTAWLQET SOBOJ RAS-

TQVENIe

PLOSKOSTI C

(PO WSEM NAPRAWLENIQM) W jaj RAZ,

POWOROT NA UGOL

arg a

I SDWIG NA WEKTOR b. w REZULXTATE

KAVDOGO IZ \TIH DEJSTWIJ L@BAQ OKRUVNOSTX PEREHODIT W

OKRUVNOSTX, A L@BAQ PRQMAQ | W PRQMU@.

w ZAPISI z = x+iy w =u+iv SOOTWETSTWIE w =

PRINI-

2;v

MAET WID x=

, y =

, L@BAQ VE PRQMAQ ILI OKRUV-

u +v

NOSTX NA PLOSKOSTI PEREMENNOJ z = x+iy ZADAETSQ URAWNE-

NIEM (x2 +y2)+ x+ y + = 0, KO\FFICIENTY

KOTOROGO | DEJSTWITELXNYE ^ISLA, POD^INENNYe USLOWI@

2 + 2 >4 .1

pODSTANOWKA x=	u		, y =	2;v	2	PREOBRAZUET \TO URAW-
	2	2
	u +v			u +v

NENIE W (u2+v2)+ u; v+ =0 (PRI \TOM 2+(; )2 >4 ),

1 w SLU^AE = 0 (URAWNENIQ PRQMOJ) POSLEDNEE NERAWENSTWO OZNA- ^AET, ^TO HOTQ BY ODNO IZ ^ISEL I NE RAWNO NUL@, A PRI 6= 0 WYRAVAET TOT FAKT, ^TO OKRUVNOSTX NE QWLQETSQ WYROVDENNOJ ILI

MNIMOJ: \TO SLEDUET IZ ZAPISI URAWNENIQ (PRI 6= 0) W WIDE

;x+ 2+;y+ 2; 22 ; 22 + =0.

2 2 4 4

T. E. W URAWNENIE PRQMOJ ILI OKRUVNOSTI (NA PLOSKOSTI PE-

REMENNOJ w = u+iv). sLU^AI PRQMOJ ( = 0) I OKRUVNOSTI

( 6= 0) SOOTWETSTWU@T PROHOVDENI@ I, NAOBOROT, NE PRO-

HOVDENI@ ISHODNOJ PRQMOJ ILI OKRUVNOSTI ^EREZ NA^ALO KOORDINAT | \OSOBU@" TO^KU FUNKCII w = z1 .

oPREDELITX, KAKIE PRQMYE I OKRUVNOSTI PEREWODQTSQ DROBNO-LINEJNOJ FUNKCIEJ w = azcz++db W PRQMYE, A KAKIE W OKRUVNOSTI, PRO]E WSEGO S U^ETOM TOGO, ^TO \OSOBAQ" TO^- KA z0 = ;dc PEREHODIT W BESKONE^NO UDALENNU@, A EE SREDI

PRQMYH I OKRUVNOSTEJ SODERVAT LI[X PRQMYE. Q.E.D.

tO^KI z1 z2 2C S^ITA@T SIMMETRI^NYMI OTNOSITELX-

NO PRQMOJ ILI OKRUVNOSTI L, ESLI WSE PROHODQ]IE ^EREZ \TI TO^KI PRQMYE I OKRUVNOSTI PERESEKA@T L POD PRQMYM UGLOM.

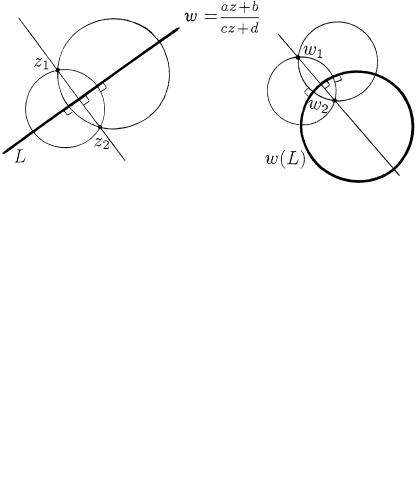
sWOJSTWO \SOHRANENIQ SIMMETRII". pRI DROBNO-

LINEJNOM OTOBRAVENII w =w(z) TO^KI z1 z2 2C , SIMMET-

RI^NYE OTNOSITELXNO PRQMOJ ILI OKRUVNOSTI L, PEREHODQT W TO^KI w1 w2, SIMMETRI^NYE OTNOSITELXNO OBRAZA w(L)

\TOJ PRQMOJ ILI OKRUVNOSTI.

rIS. 27

dOKAZATELXSTWO. pUSTX z1 z2 | TO^KI, SIMMETRI^NYE

OTNOSITELXNO PRQMOJ ILI OKRUVNOSTI L, I w = w(z) | DROBNO-LINEJNAQ FUNKCIQ, PEREWODQ]AQ IH, SOOTWETSTWEN-

NO, W TO^KI w1 w2 I PRQMU@ ILI OKRUVNOSTX (\KRUGOWOE"

SWOJSTWO!) w(L). tREBUETSQ DOKAZATX, ^TO ESLI PRQMAQ ILI OKRUVNOSTX L PROHODIT ^EREZ TO^KI w1 w2 , TO ONA PERE- SEKAET LINI@ w(L) POD PRQMYM UGLOM (RIS. 27). nO OBRATNYM OTOBRAVENIEM z = z;1(w), TAKVE QWLQ@]IMSQ DROBNO-

LINEJNYM (S. 90), PRQMAQ ILI OKRUVNOSTX L PEREWODITSQ W

PRQMU@ ILI OKRUVNOSTX, PROHODQ]U@ ^EREZ TO^KI z1 z2, A SLEDOWATELXNO, PERESEKA@]U@ PRQMU@ ILI OKRUVNOSTX L POD PRQMYM UGLOM. oSTAETSQ PRIMENITX SWOJSTWO KON- FORMNOSTI (S. 92), W SILU KOTOROGO PRQMYM QWLQETSQ I UGOL

PERESE^ENIQ LINIJ L I w(L). Q.E.D.

OPREDELENIE SIMMETRII TO^EK z1 z2 2 C OTNOSITELX- NO PRQMOJ ILI OKRUVNOSTI L, PRED[ESTWU@]EE FORMULI- ROWKE \KRUGOWOGO" SWOJSTWA, W SLU^AE PRQMOJ RAWNOSILXNO OBY^NOMU: TO^KI z1 I z2 SLUVAT KONCAMI OTREZKA, PERPENDIKULQRNOGO PRQMOJ L I PERESEKAEMOGO E@ W EGO SEREDINe. eSLI VE L | OKRUVNOSTX, TO SIMMETRI^NYMI OTNOSITELX-

NO NEE QWLQ@TSQ: a) CENTR O OKRUVNOSTI L I BESKONE^NO UDALENNAQ TO^KA B) TO^KI z1 I z2, LEVA]IE NA LU^E, WY- HODQ]EM IZ TO^KI O, I OTSTOQ]IE OT NEE NA RASSTOQNIQ,

PROIZWEDENIE KOTORYH RAWNO KWADRATU RADIUSA OKRUVNOS-

TI L (\PROIZWEDENIE SEKU]EJ NA EE WNE[N@@ ^ASTX RAWNO KWADRATU KASATELXNOJ" RIS. 28).

nAPRIMER, SIMMETRI^NYMI OTNOSITELXNO DEJSTWITELXNOJ OSI QWLQ@TSQ PARY KOMPLEKSNO-SOPRQVENNYH ^ISEL z

I z (TO^NEE, IZOBRAVA@]IH IH TO^EK). sIMMETRI^NYMI OTNOSITELXNO OKRUVNOSTI RADIUSA 1 S CENTROM W NA^ALE


1				1			1				);1 (TAK KAK
KOORDINAT QWLQ@TSQ: a) 0 I								B) z I	(	z	);1 (TAK KAK
arg(		); = arg z,	a	(		); jzj = 1).
arg(	z	); = arg z,	a	(	z	); jzj = 1).

rIS. 28

kAKOWY BY NI BYLI TRI (RAZNYE) TO^KI z1 z2 z3 2 C I TRI (RAZNYE) TO^KI w1 w2 w3 2 C , SU]ESTWUET (I PRI-

TOM EDINSTWENNAQ) PRQMAQ ILI OKRUVNOSTX L, KOTORAQ

PROHODIT ^EREZ TO^KU z3 I OTNOSITELXNO KOTOROJ TO^KI z1 I z2 SIMMETRI^NY.

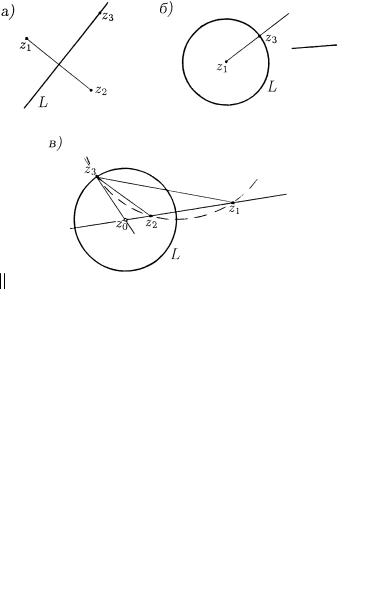
rIS. 29

dOKAZATELXSTWO. eSLI z3 = 1 ILI VE WSE TRI TO^KI z1 z2 z3 KONE^NY, PRI^EM DWE PERWYH RAWNOUDALENY OT TRETXEJ, TO L | \TO PRQMAQ, KOTORAQ PERPENDIKULQRNA K SOEDINQ@]EMU TO^KI z1 I z2 OTREZKU I DELIT EGO POPOLAM (RIS. 29, A).

eSLI BESKONE^NO UDALENNOJ QLQETSQ ODNA IZ TO^EK z1 z2 (NAPRI- MER, z2 ), TO L | \TO PROHODQ]AQ ^EREZ TO^KU z3 OKRUVNOSTX S CENTROM

z1 (RIS. 29, B).

eSLI z1 z2 z3 2 C , A IZ ZNA^ENIJ a = jz1 ;z3j I b = jz2 ;z3j ODNO (K PRIMERU, PERWOE) BOLX[E DRUGOGO, TO L | \TO OKRUVNOSTX, CENTR

z0 KOTOROJ LEVIT NA PRQMOJ, PROHODQ]EJ ^EREZ TO^KI z1 I z2 (BLIVE KO WTOROJ IZ NIH). ESLI PRI \TOM z3 NE LEVIT NA \TOJ VE PRQMOJ, TO z0 ESTX Ta EE TO^KA, W KOTOROJ \TU PRQMU@ PERESEKAET KASATELXNAQ, PROWEDENNAQ IZ TO^KI z3 K OKRUVNOSTI, PROHODQ]EJ ^EREZ TO^KI

z1 z2 z3 (RIS. 29, W). eSLI VE TO^KI z1 z2 z3 LEVAT NA ODNOJ PRQMOJ, TO CENTR z0 OKRUVNOSTI L UDALEN OT TO^KI z1 NA RASSTOQNIE

a2=(a b) | SOOTWETSTWENNO TOMU, LEVIT TO^KA z3 MEVDU ILI PO ODNU STORONU OT TO^EK z1 z2. Q.E.D

wOT NESKOLXKO ZADA^, RE[AEMYH PRIMENENIEM SWOJSTW

DROBNO-LINEJNYH OTOBRAVENIJ.

1. zADANNU@ PRQMU@ (OKRUVNOSTX) PEREWESTI DROBNO- LINEJNOJ FUNKCIEJ W ZADANNU@ PRQMU@ (OKRUVNOSTX).

dOSTATO^NO, WZQW (PROIZWOLXNO) NA OBEIH LINIQH PO TRI TO^KI z1 z2 z3 I w1 w2 w3, POSTROITX DROBNO-LINEJNU@

FUNKCI@ SOGLASNO FORMULE

w;w1 w3;w2 z;z1 z3;z2 w;w2 w3;w1 = z;z2 z3;z1 ,

POSLE ^EGO WOSPOLXZOWATXSQ \KRUGOWYM" SWOJSTWOM I TEM, ^TO PRQMAQ ILI OKRUVNOSTX POLNOSTX@ OPREDELQETSQ ZADA- NIEM L@BYH TREH Ee TO^EK.

2. nAJTI FUNKCI@, WZAIMNO ODNOZNA^NO I KONFORMNO OTOBRAVA@]U@: A) WNUTRENNOSTX OKRUVNOSTI, B) WNE[-

NOSTX OKRUVNOSTI (S WKL@^ENIEM W NEE TO^KI 1), W) POLUPLOSKOSTX (^ASTX PLOSKOSTI, LEVA]EJ PO ODNU STORONU OT PRQMOJ) NA L@BU@ OBLASTX G IZ \TOGO VE SPISKA.

zAME^ANIE. kAK BUDET USTANOWLENO NIVE (XVIII, S. 307{ 308), DRUGIH (POMIMO DROBNO-LINEJNYH) FUNKCIJ, DA@]IH RE[ENIQ ZADA^ \TOGO I SLEDU@]EGO PUNKTOW, NE SU]ESTWU-

ET.

rIS. 30

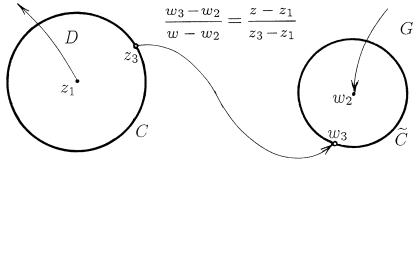
pUSTX, K PRIMERU, D | WNUTRENNOSTX OKRUVNOSTI C,

a G | WNE[NOSTX OKRUVNOSTI C. wZQW TO^KI z1 z2 z3

w1 w2 w3 | WNE, WNUTRI I NA OKRUVNOSTIe Ce, PRI^EM TAK, ^TOBY TO^KI z1 I z2 BYLI SIMMETRI^NY OTNOSITELXNO C, a w1 I w2 | OTNOSITELXNO Ce (W KA^ESTWE z1 I w2 MOVNO WZQTX CENTRY OKRUVNOSTEJ C I Ce, A W KA^ESTWE z2 I w1 | BES-

SOOTWETSTWENNO WNUTRI, WNE I NA OKRUVNOSTI C, A TO^KI

KONE^NOSTX RIS. 30), SLEDUET POSTROITX DROBNO-LINEJNU@

FUNKCI@ KAK W PREDYDU]EM PUNKTE. oSTAETSQ ZAMETITX, ^TO TO^KI, LEVA]IE PO ODNU STORONU OT OKRUVNOSTI , NE MOGUT PEREJTI W TO^KI, LEVA]IE PO RAZNYE STORONY OT OKRUVNOSTI Ce: L@BYE DWE TO^KI IZ WNE[NOSTI OKRUVNOSTI C MOVNO SOEDINITX LOMANOJ, NE PERESEKA@]EJ \TU OKRUVNOSTX, A OB-

RAZ \TOJ LOMANOJ PRI DROBNO-LINEJNOM OTOBRAVENII ESTX

(W SILU \KRUGOWOGO" SWOJSTWA) \LOMANAQ" (IZ DUG OKRUVNOS-

TEJ), NE PERESEKA@]AQ OKRUVNOSTI C. (rAZBOR DRUGIH SLU-

^AEW OBLASTEJ D I G PROWODITSQ POe\TOJ VE SHEME.)

3. nAJTI OB]IJ WID DROBNO-LINEJNYH FUNKCIJ, OTOBRA-

VA@]IH:

KRUG

2C :

jzj< 1

NA KRUG

2C : jwj < 1

(ILI,

KAK GOWORQT,

EDINI^NYJ KRUG \NA SEBQ")

POLUPLOSKOSTX

z 2 C : Im z > 0

NA POLUPLOSKOSTX

C : Im w >0

(WERHN@@ POLUPLOSKOSTX \NA SEBQ")

WERHN@@ POLUPLOSKOSTX NA EDINI^NYJ KRUG.

l@BOE DROBNO-LINEJNOE OTOBRAVENIE KRUGA

jzj

< 1

KRUG

(PUNKT a) PREOBRAZUET OKRUVNOSTX

<1,

OKRUVNOSTX

= 1 . tAK KAK NEKOTORAQ TO^KA

PEREHODIT W 0,

SIMMETRI^NAQ EJ

(OTNOSITELXNO OKRUVNOSTI

jzj

1. pOSKOLXKU

z2 = z(z1);

= 1 ) TO^Ka z2 PEREHODIT W

PRI

= 0 I

PRI z1 = 0,

TO (S U^ETOM ZAME^ANIQ NA

z;z1

S. 92) W OBOIH SLU^AQH

w =

, GDE

| NENULEWOE KOMP-

1;z1 z

LEKSNOE ^ISLO.

pODSTANOWKA z = 1 POZWOLQET ZAKL@^ITX:

=1,

A SLEDOWATELXNO, w =ei

;z1

R .

1;z1 z

j j

|TA VE SHEMA RASSUVDENIJ PRIMENITELXNO K PUNKTAM B)

I W) DAET OTWETY: B)

w;w1

= ei

;W)

w = ei

z;z1 , GDE

w;w1

z;z1

z1 I w1 | TO^KI WERHNEJ PoLUPLOSKOSTI,

| DEJSTWI-

TELXNoe ^ISLo.

oTWET K PUNKTU B) MOVNO PREDSTAWITX I W DRUGOJ FORME. fUNKCIQ

w =

az+b

, OTOBRAVA@]AQ POLUPLOSKOSTX

Imz > 0

NA POLUPLOS-

cz+d

, TO^KI DEJSTWITELXNOJ OSI DOLVNa PEREWODITX W

KOSTX

Im w > 0

TO^KI DEJSTWITELXNOJ OSI. OTc@DA SLEDUET, ^TO (S TO^NOSTX@ DO OB-

]EGO NENULEWOGO MNOVITELQ) KO\FFICIENTY a b c d DOLVNY BYTX

DEJSTWITELXNYMI. tREBOWANIE, ^TOBY ZNA^ENIQM z c			Im z > 0 SOOT-
WETSTWOWALI ZNA^ENIQ w c Im w >0, W ZAPISI z =x+iy OZNA^AET:
0 < Im a(x+iy)+b =	(ad;bc)y	PRI y > 0, T.E.	a b	>0.
			c d
c(x+iy)+d	(cx+d)2+(cy)2

100

oTOBRAVA@]IE SWOJSTWA FyNKCII w = 12;z + z1

|TA FUNKCIQ (W OTE^ESTWENNOJ LITERATURE IMENUEMAQ

FUNKCIEJ vUKOWSKOGO1) NE QWLQETSQ DROBNO-LINEJNOJ, NO,

OTLI^AQSX PO SWOJSTWAM, BLIZKA K NIM PO ROLI W PRAKTIKE

KONFORMNYH OTOBRAVENIJ.

rAZRE[IMOSTX URAWNENIQ

w =

z +

OTNOSITELXNO z

PRI L@BOM w

C GOWORIT O TOM,

^TO FUNKCIQ vUKOWSKOGO

;

(ZNA^ENIQM

OTOBRAVAET PLOSKOSTX C NA WS@ PLOSKOSTX C

z =0 I z =1 OTWE^AET w =

1). TAK KAK w0 =

, KON-

FORMNOSTX \TOGO OTOBRAVENIQ GARANTIROWANA WO WSEH OT-

LI^NYH OT 0 I

1 TO^KAH z 2 C .2

;

B OTLI^IE OT DROBNO-LINEJNYH, oTOBRAVENIE FUNKCIEJ

w =

z +

NE QWLQETSQ WZAIMNO-ODNOZNA^NYM: ZNA^ENIQM

DLQ

z = z1; z2,

KOTORYH z1 z2 = 1, OTWE^AET ODNO I TO VE

ZNA^ENIE w. pO-DRUGOMU \TO MOVNO WYRAZITX SLOWAMI: OB-

RATNOJ PO OTNO[ENI@ K FUNKCII w =

z +

QWLQETSQ DWU-

1 (GDE I KAK MOVNO WYDELITX

ZNA^NAQ FUNKCIQ z =w+ w

;

EE ODNOZNA^NYE WETWI, UKAZANO W

IV NA c. 69).

sUTX OTOBRAVENIQ w =

z +

PROQSNITSQ, ESLI PROSLE-

DITX ZA OBRAZAMI TO^EK OKRUVNOSTEJ RADIUSOW r >1 S CENT-

;

ROM z = 0. zAPISX z = reit

= r(cos t + i sin t)

w = u + iv,

PRIWODIT K SOOTNO[ENIQM

u+iv = 2

+ reit

= 2

r(cos t+i sin t)+ r (cos t

;

i sin t) =

;

2;r + r

cos t + i 2;r ; r

sin t,

1 nIKOLAJ eGOROWI^ vUKOWSKIJ

(1847 {1921) | ROSSIJSKIJ MEHA-

NIK, DLQ KOTOROGO \TA FUNKCIQ POSLUVILA OTPRAWNYM PUNKTOM W RAZ- RABOTKE TEORII POD_EMNOJ SILY KRYLA SAMOLETA.

2 nA SAMOM DELE KONFORMNOSTX IMEET MESTO I W \OSOBYH" TO^KAH 0 I 1, ESLI PEREMENNYE z I w OTME^ATX NA SFERE rIMANA.

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 3610 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
16.08.201320 Mб209Харитонов Енергетика.pdf
#
16.08.20137.37 Mб219Хлопкин Морская атомная енергетика 2007.pdf
#
16.08.20132.03 Mб69Цывкунова Интернатионал Лаw Учебно-методическое пособие 2010.pdf
#
16.08.2013673.64 Кб68Цыганова Современная нормативная документация 2008.pdf
#
16.08.201315.92 Mб146Чернов Влияние легирования 2007.pdf
#
16.08.201351.53 Mб84Шведенко Начала анализа функций комплексной переменной 2008.pdf
#
16.08.201310.65 Mб1660Шелегов Насосное оборудование АЕС 2011.pdf
#
16.08.20133.17 Mб1070Шелегов Физические особенности и конструкция Реактора РБМК-1000 2007.pdf
#
16.08.20138.21 Mб333Шишкин Основы проектирования станочных приспособлений 2010.pdf
#
16.08.201311.25 Mб313Шмаков Основы металловедения 2007.pdf
#
16.08.20132.35 Mб115Шмелев Физические основы обезвреживания 2008.pdf