
Жданов Основы физических процессов 2007
.pdf
ние частицы по окружности можно уподобить круговому току j = qω/2π, то вращению частицы в магнитном поле можно сопоставить магнитный момент, равный магнитному моменту этого кругового тока:
r |
j |
r |
|
μ = |
|
S . |
(2.8) |
c |
Здесь S - соответственно ориентированная площадь круга, охватываемая ларморовской окружностью, равная S = πρ2. Подставляя значения j и S в уравнение (2.8), получаем
r |
B |
, |
|
mv2 / 2 |
|
|
μ = −μ |
|
μ = |
|
. |
(2.9) |
|
B |
B |
Магнитный момент вращающейся в магнитном поле частицы всегда направлен против магнитного поля, следовательно, положительно и отрицательно заряженные частицы вращаются в противоположных направлениях (рис. 2.1). В общем случае траектория движения частицы в постоянном и однородном магнитном поле представляет собой спираль.
Рис.2.1. Движение заряженных частиц в постоянном магнитном поле (продольная скорость направлена вдоль магнитного поля в обоих случаях)
Конкретное направление вращения частицы в магнитном поле соответствует известному «правилу Ленца», согласно которому, любая механическая система стремится двигаться так, чтобы противодействовать причине, вызывающей ее движение. Вращающаяся по ларморовской окружности частица ведет себя как диамагнетик − она стремится ослабить охватываемый её ларморовской окружностью поток внешнего магнитного поля. Это выражает суть так называемого принципа диамагнетизма свободных частиц.
81

Возникает «законный» вопрос: если бы вращение частицы по ларморовской окружности вызывало изменение магнитного поля, в котором она вращается, то это должно было бы сказываться на траектории её движения, а изменение траектории в свою очередь привело бы к дополнительному искажению поля и т.д. В действительности, это ложный путь. В электродинамике постулируется, что точечные заряженные частицы взаимодействуют друг с другом через посредством электромагнитного поля, создаваемого ими в окружающем пространстве, тем самым «самодействие» частиц исключается. Например, в рассмотренном случае движения выделенной частицы в заданном магнитном поле предполагается, что это поле создается другими, движущимися заданным образом заряженными частицами, здесь унесенными на бесконечность. По этой причине влиянием рассматриваемой частицы на движение источников магнитного поля можно пренебречь, − а только так, влияя на траектории этих источников, и затрачивая соответствующую энергию, частица могла бы «управлять» своей траекторией.
§ 14. Движение в сильном медленно меняющемся поле. Дрейфовое приближение
Если магнитное поле медленно меняется в пространстве и во времени, то, движущаяся в нем частица, прежде чем почувствует влияние изменения поля, совершит в нем множество ларморовских оборотов, навиваясь на силовую линию магнитного поля. Это движение, фактически в постоянном поле, мы уже изучили. Поэтому можно рассматривать движение не собственно частицы, а её мгновенного центра вращения, так называемого ведущего центра (в зарубежной литературе такой подход известен как приближение ве-
дущего центра - guiding center approximation). Следует, однако,
иметь в виду, что в случае, если магнитное поле меняется во времени, то нужно учитывать и слабые электрические поля. Согласно уравнениям Максвелла, в силу
rotEr = − 1c ∂∂Bt ,
переменное во времени магнитное поле вызывает появление вихревого электрического поля.
На медленное движение ведущего центра, определяемого как продольной скоростью частицы, так и влиянием слабого электрического поля и слабых неоднородностей магнитного поля, наложится быстрое вращение частицы вокруг силовых линий магнитного поля. Такое раздельное рассмотрение быстрого вращения частицы по ларморовской окружности и медленного «дрейфа» центра
82

этой окружности будет справедливо, если изменение ларморовского радиуса на одном обороте будет существенно меньше самого ларморовского радиуса. Это условие, очевидно, будет выполнено, если характерное время изменения полей будет значительно больше времени ларморовского оборота, и если характерный пространственный масштаб изменения полей будет значительно превышать ларморовский радиус:
t ха р |
>> T |
, l ха р |
>> ρ |
ла рм |
. |
поля |
ла рм |
поля |
|
|
Количественно эти критерии можно сформулировать следующим образом:
∂ B ∂ t |
|
|
|
∂ E ∂ t |
|
|
|
||
ωларм B |
<< 1 , |
ωла рм E << 1 , |
|
||||||
B |
|
<< 1, |
|
|
E |
|
<< 1 . |
|
|
|
|
|
|
||||||
ρларм B |
|
|
|
|
ρла рм E |
|
(2.10) |
||
Очевидно, эти условия выполнены тем лучше, чем больше величина напряженности магнитного поля, так как ларморовская частота вращения частицы возрастает прямо пропорционально величине магнитного поля, а ларморовский радиус убывает обратно пропорционально величине магнитного поля. Вместе с тем, величина напряженности электрического поля E не должна быть слишком большой. На одном обороте частицы ее скорость должна меняться незначительно, настолько незначительно, чтобы выполнялось условие
δv ~ |
qE |
T |
~ |
qE |
≡ c |
E |
<< v . |
|
|
B |
|||||
|
m ла рм |
|
mωла рм |
|
|||
Откуда и получаем требуемое ограничение на величину напряженности электрического поля
v |
|
|
E << c |
B . |
(2.11) |
При выполнении условий (2.10) и (2.11) истинная траектория частицы обычно представляет собой медленно изгибающуюся спираль с медленно меняющимся радиусом и шагом. Проекция траектории частицы на плоскость, перпендикулярную к силовым линиям магнитного поля, представляет собой трохоиду.
83
Движение ведущего центра обычно называют дрейфовым движением, а приближенное описание движения частицы как движение ведущего центра - дрейфовым приближением. Рассмотрим некоторые случаи, представляющие общий интерес, так как к ним можно свести многие виды движения заряженных частиц в неоднородных магнитных полях и в полях других внешних сил.
§ 15. Движение частицы в однородном магнитном поле под действием постоянной силы
Еслиrна частицу, помимо силы Лоренца, действует постоянная сила F , то уравнение движения частицы имеет вид:
r |
|
q r |
r r |
|
|
mv |
= |
|
v |
× B + F . |
(2.12) |
c |
|||||
& |
|
|
|
|
|
Разложив векторы v и F на перпендикулярную и параллельную магнитному полю компоненты, как это уже делалось в предыдущем параграфе, определим, что
r& |
r |
r |
q r r |
|
|
mv|| = F|| , |
mv = F + |
|
v × B . |
(2.13) |
|
c |
|||||
|
& |
|
|
|
|
Мы видим, что продольное и поперечное движения частицы оказываются независимыми, и их можно рассмотреть раздельно. При этом составляющая силы, параллельная магнитному полю, обуславливает ненулевое продольное ускорение частицы, которое изменяет продольную компоненту скорости. Под действием составляющей силы, перпендикулярной к магнитному полю, частица совершает сложное движение, являющееся суперпозицией вращения частицы и систематического сноса (дрейфа) с некоторой постоянной скоростью. Чтобы убедиться в этом, представим скорость поперечного движения в виде суммы
vr = vrd + vrr , |
(2.14) |
где vrd — постоянная скорость, аvrr — скорость вращения вокруг
ведущего центра. Такое представление можно интерпретировать и как переход в движущуюся с постоянной, но заранее неизвестной (!), скоростью систему координат. Подстановка выражения (2.14) во вторую из формул (2.13) дает
84

r |
r r |
q r r |
q r r |
|
||
mv ≡ mvr = F + |
|
vd × B + |
|
vr × B . |
(2.15) |
|
c |
c |
|||||
& |
& |
|
|
|
|
|
Так как первые два слагаемых справа − постоянные векторы, то они могут компенсировать друг друга. Это позволяет потребовать выполнение равенства
Fr + qc vrd × Br = 0 .
Это требование и определяет величину скорости дрейфа
частицы: |
|
|
|
|
|
|
|
|
r |
|
c F × B |
|
|
||||
vd |
= |
|
|
|
|
|
. |
(2.16) |
q |
|
B2 |
||||||
Оставшаяся часть уравнения (2.15) |
|
|
||||||
r |
|
|
e r |
r |
|
|||
mvr = |
|
vr × B , |
(2.17) |
|||||
c |
||||||||
& |
|
|
|
|
|
|
|
|
описывает вращение вокруг ведущего центра, как это очевидно из сравнения с уравнением (2.5). Скорость частицы в таком движении, как мы уже обсуждали в предыдущем параграфе, может только поворачиваться по направлению, не меняясь по абсолютной величине. Величина скорости вращения может быть найдена по начальной скорости частицы, которая, конечно, должна быть изначально задана:
vr =|vr 0 − vrd | , |
(2.18) |
гдеvr 0 - поперечная по отношению к магнитному полю компонента начальной скорости. Например, в частном случае vr 0 = 0 получаем
vr = vd = |
cF |
|
. |
(2.19) |
|
qB |
|||||
|
|
|
|||
Модуль скорости вращения определяет радиус окружности:
ρ = |
mcvr |
. |
(2.20) |
|
|||
|
qB |
|
|
85
по которой вращается частица в подвижной системе координат, движущейся со скоростью (2.16).
Не составляет большого труда найти и точный закон поперечного движения частицы:
r |
r |
|
r |
|
|
(vr 0 |
− vrd ) × B |
|
|
|
r |
= r |
+ v |
d |
t + |
|
|
(1 |
− cosωt) + |
|
|
|
|
|
||||||||
|
0 |
|
|
|
|
ωB |
|
|
|
|
|
vr 0 − vrd |
|
|
|
|
|
. |
(2.21) |
||
|
|
|
|
|
|
|
||||
+ |
sinωt |
|
|
|
|
|||||
|
|
|
|
|
||||||
|
ω |
|
|
|
|
|
|
|
|
|
Индексом ноль здесь помечены начальные значения соответствующих величин.
Составить представление о разнообразии возможных траекторий поперечного движения можно по рис. 2.2.
Кроме того, следует отметить, что если поперечная компонента начальной скорости в точности совпадает со скоростью дрейфа:
vr 0 = vrd , |
(2.22) |
то, как это следует из закона движения, частица движется равномерно поперек магнитного поля. Такая возможность представляет большой интерес в проблеме транспорта частиц поперек сильного магнитного поля.
Намиr не высказывалось никаких предположений о природе силы F , поэтому выводr о характере движения справедлив для любой
постоянной силы F : продольное (в общем случае) ускорение и систематический снос с постоянной скоростью в совокупности с равномерным вращением в поперечной по отношению к магнитному полю плоскости.
Из формулы (2.16) следует, что скорость дрейфа не зависит от массы частицы, но зависит от знака ее заряда, если сила от знака заряда не зависит. Полезно отметить также, что действие постоянной силы, перпендикулярной к магнитному полю, приводит (в среднем по осцилляциям!) не к увеличению скорости частицы, а к движению ее перпендикулярно к магнитному полю с постоянной скоростью. С похожим явлением мы встречаемся в механике при изучении прецессии оси гироскопа, когда приложенный к гироскопу момент вызывает вращение его оси в направлении, перпендикулярном как к моменту количества движения гироскопа, так и к моменту силы.
86
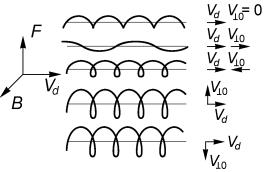
Рис.2.2. Типы возможных траекторий для некоторых частных случаев направления начальной скорости поперечного движения частицы в скрещенных полях (штриховая линия − положение центра ларморовской окружности)
§ 16. Дрейф заряженных частиц вдоль плоскости скачка магнитного поля
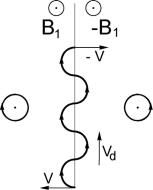
В качестве еще одного точно разрешимого примера с дрейфовым движением рассмотрим задачу о движении заряженной частицы в магнитном поле со скачком, слева и справа от плоскости которого магнитное поле однородно и одинаково направлено, но имеет разную величину (см. рис. 2.3), пусть справа будет В2>В1. Вне скачка, где поле однородно, на расстоянии, превышающем ларморовский радиус, частицы описывают окружности, размер которых больше в области слабого поля (слева на рис.2.3).
На меньшем расстоянии при движении частицы её ларморовская окружность пересекает плоскость скачка, характер её движения резко меняется, так как каждый раз после пересечения этой плоскости скачком изменяется радиус окружности. Траектория приобретает сложный характер с наличием систематического «сноса» частицы вдоль плоскости скачка. Как видно из рисунка, дрейф перпендикулярен направлению магнитного поля и его градиента, причем, очевидно, имеет противоположный знак для разноименно заряженных частиц: для геометрии рис.2.3 он направлен вверх для положительного заряда, или был бы направлен вниз, если бы заряд был отрицательным.
87
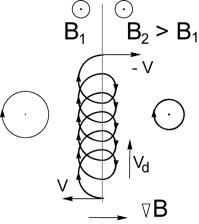
Рис.2.3. Схема возникновения дрейфа положительного заряда на границе со скачком величины магнитного поля
Нетрудно подсчитать скорость этого дрейфа. Пусть для простоты частица пересекает плоскость скачка по нормали. Тогда за время, равное сумме ларморовских полупериодов для области слева и справа
t = T |
+ T = |
|
π |
|
+ |
|
π |
|
, |
(2.23) |
|
|
ω |
|
ω |
|
|||||||
1 |
2 |
|
1 |
|
2 |
|
|
||||
где |
|
|
|
|
|
|
|
|
|
||
|
|
|
qB1,2 |
|
|
|
|
||||
|
ω 1,2 |
= |
, |
|
|
|
|||||
|
|
|
|
|
|||||||
|
|
|
|
|
mc |
|
|
|
|
|
|
циклотронные частоты, вычисленные по значению поля слева и справа от плоскости скачка. Частица смещается вдоль этой плоскости на длину
x = 2( ρ1− ρ 2 ) = 2( |
v |
|
− |
v |
|
) . |
(2.24) |
|
ω |
1 |
ω |
2 |
|||||
|
|
|
|
Здесь v − скорость частицы, которая предполагается изначально направленной перпендикулярно плоскости скачка. Очевидно, скорость дрейфа можно определить как
vd = |
x = |
2v |
|
B2 |
− B1 |
≡ |
v B |
, |
(2.25) |
|||
|
|
|
|
|
|
|||||||
π B2 |
+ B1 |
π < B > |
||||||||||
|
t |
|
|
|
||||||||
|
|
|
|
|
|
88 |
|
|
|
|
|
|
где В=В2−В1 − величина скачка магнитного поля, а <В>=(В2+В1)/2 − его среднее значение. Подчеркнем, что полученное решение − точное, причем в условиях, когда дрейфовое приближение заведомо неприменимо: размер неоднородности, как предполагается, должен быть значительно меньше, чем ларморовские радиусы частиц!
Величина скорости дрейфа зависит, очевидно, и от угла, под которым частица пересекает область скачка. Мы не будем останавливаться на этом интересном вопросе − эту зависимость несложно получить, по сути дела, тем же самым путем, как и рассмотренный выше более простой случай перпендикулярного пересечения. Дрейф возникает и том случае, когда слева и справа от некоторой плоскости магнитное поле по величине не меняется, но изменяет направление (см. рис.2.4). Магнитная конфигурация такого типа возникает в так называемых токовых слоях.
В центре симметричного, например, плоского токового слоя магнитное поле равно нулю, а вне этой центральной плоскости, как это следует из закона
r |
4π r |
|
Ампера rot B = |
|
j , меняет знак. Если толщиной слоя пренебречь, полу- |
c |
||
чим скачок направления поля.
Вне слоя частицы вращаются по ларморовским окружностям, здесь − одинакового радиуса, но с противоположным направлением вращения, и дрейфа нет, если расстояние от плоскости слоя превышает ларморовский радиус.
Рис.2.4. Дрейф положительного заряда при смене направления магнитного поля
Дрейф возникает, когда ларморовская окружность пересекает эту плоскость. Траекторию частицы можно получить следующим образом. Пусть пересечение плоскости слоя частицей – по нормали, тогда ларморовскую окружность следу-
89
ет «разрезать» вдоль вертикального диаметра и затем, для положительного заряда, правую половину следует отразить зеркально вверх, как это изображено на рис.2.4. При этом за ларморовский период смещение вдоль слоя, очевидно, составляет два ларморовских диаметра, так что скорость дрейфа для этого случая:
vd = |
x |
= |
4ρ |
= |
4v / ω |
= |
2 |
v . |
(2.26) |
t |
T |
2π / ω |
|
||||||
|
|
|
|
π |
|
||||
При пересечении «общего положения», при произвольном угле, скорость дрейфа, очевидно, меняется с изменением угла, но не зависит от величины магнитного поля! Подчеркнем, что и в этом случае дрейфовое приближение неприменимо.
§17. Важнейшие типы дрейфовых движений частиц в плазме
Рассмотренный в §15 пример движения частиц в магнитном поле под действием дополнительной постоянной силы является точным решением нерелятивистских уравнений движения. Весьма важным является то, что закономерности, присущие этому движению, сохраняются и в случае, когда поля, действующие на частицу, являются переменными. Однако характерные масштабы их изменения во времени и по пространству должны быть, как уже обсуждалось, достаточно медленными в сравнении с ларморовским периодом осцилляций частицы и ларморовским радиусом описываемой ею окружности соответственно. В этом случае для скорости дрейфа вновь справедлива формула (2.16). С тем лишь существенным отличием, что скорость дрейфа должна быть достаточна мала, значительно меньше средней скорости хаотического движения частиц плазмы. Последняя, как известно, определяется тепловой скоростью частиц. Таким образом, приходим к условию
vd << vT , |
(2.27) |
ограничивающему, причем зачастую весьма существенно, область применимости дрейфового приближения в описании движения частиц плазмы. Предполагая указанные ограничения выполненными, рассмотрим кратко некоторые примеры дрейфовых движений плазмы.
90
