
Жданов Основы физических процессов 2007
.pdf
Формально это отвечает пределу mi→∞, и уравнение (4.45) упрощается:
|
|
ωpe2 |
|
|
|
|
|
T |
|
1 − |
|
|
|
= 0, |
c2 |
= γ |
|
e |
. |
ω2 |
− k |
2c2 |
|
||||||
|
|
s e |
|
e m |
|||||
|
|
|
se |
|
|
|
|
e |
|
Теперь его уже не сложно решить, и мы, вновь выбирая положительный корень, получаем:
ω = ωpe2 + k 2cse2 . |
(4.46) |
Это соотношение и определяет закон дисперсии ленгмюровской волны в плазме с конечной температурой.
Любопытно отметить, что это соотношение по виду оказывается вполне аналогичным известной формуле, определяющей связь энергии и импульса релятивистской частицы:
ε = (mc2 )2 + p2 c2 .
По этой причине о законе дисперсии (4.46) говорят как о «частицеподобном», а ленгмюровские волны в этом плане являются «квазичастицами», которые принято называть плазмонами.
Полезно отметить также, что закон дисперсии (4.46) можно записать в виде:
ω = ω |
pe |
1 +γ |
e |
k 2r2 . |
(4.47) |
|
|
De |
|
Второе слагаемое под корнем будет больше или порядка единицы, когда длина волны будет меньше дебаевского радиуса. В этом случае ленгмюровская волна сильно поглощается за счет механизма бесстолкновительного поглощения Ландау, так как оказывается резонансной по отношению к электронам плазмы,
vф ~ vTe .
По этой причине ленгмюровские волны могут существовать в плазме без существенного поглощения лишь в обратном пределе, когда их длина волны меньше дебаевского радиуса. В этом случае в (4.47) второе слагаемое под корнем можно считать малым и разложить по этой малости:
171
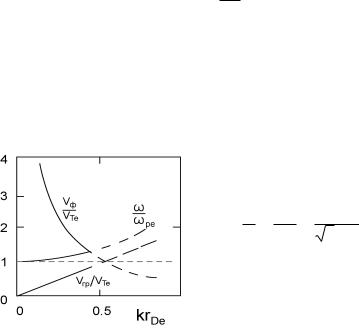
ω ≈ ω |
|
+ |
γ |
e k 2r2 |
|
, k 2r2 |
<< 1 . |
|
1 |
|
|
||||||
|
pe |
|
2 |
De |
De |
|
||
Аналогия с энергией частицы опять остается в силе, но теперь в нерелятивистском пределе, когда энергия связана с импульсом следующим образом:
ε ≈ mc2 + p2 . 2m
В области частот ленгмюровских волн гидродинамическое описание, следствием которого фактически является закон (4.47), будет адекватным при выборе γe = 3 . Подставив это значение в
(4.47), получим окончательно
|
|
|
3 |
k 2 r2 |
|
k 2 r2 |
<< 1 . |
|
|
|
|
|
ω ≈ ω |
1 |
+ |
|
, |
|
|
|
(4.48) |
||||
2 |
|
|
|
|||||||||
|
pe |
|
De |
De |
|
|
|
|
|
|
||
|
|
|
|
|
|
фазовая |
|
|
же |
|
скорость |
|
|
|
|
|
|
|
приближенно |
|
определяется |
||||
|
|
|
|
|
|
формулой |
|
|
|
|
||
|
|
|
|
|
|
vф = |
ω |
≈ |
ωpe |
= |
vTe |
. (4.50) |
|
|
|
|
|
|
k |
k |
|
||||
|
|
|
|
|
|
|
|
|
3krDe |
|||
При учете теплового движения частиц ленгмюровские волны получают возможность распространяться в плазме, перенося энергию.
Именно об этом соотношении и говорят обычно как о законе дисперсии ленгмюровских волн
в плазме. Строго говоря, он справедлив, как мы видели, лишь при выполнении сильного неравенства k 2rDe2 <<1. Однако качественно закон дисперсии (4.48) остается в силе и при выполнении более
172

мягкого условия, когда длина волны составляет несколько дебаевских радиусов.
Второе слагаемое в скобках в формуле (4.48) принято называть тепловой поправкой. Учет этой поправки приводит к тому, что групповая скорость ленгмюровской волны, в отличие от случая холодной плазмы, становится ненулевой (см. рис.4.3):
vгр = |
dω |
r 2 |
(4.49) |
r |
= 3ωpekrDe = 3vTekrDe , |
||
|
dk |
|
|
§ 32. Ионные ленгмюровские волны. Ионно-звуковые волны в плазме
Вернемся вновь к дисперсионному уравнению (4.45). Для рассмотренных выше ленгмюровских волн групповая и фазовая скорости удовлетворяют неравенству
vгр < vTe < vф .
Теперь рассмотрим возможность распространения в плазме волн, фазовая скорость которых значительно меньше тепловой скорости электронов:
vф << vTe .
Если это условие выполнено, то в уравнении (4.45) в знаменателе
второго слагаемого можно опустить ω2 и тогда это уравнение приводится к виду
|
ωpe2 |
|
|
ωpi2 |
|
|
|
|
T |
||
1 + |
|
|
− |
|
|
= 0, |
c2 |
= γ |
|
e,i |
. |
k 2c |
2 |
ω2 |
− k 2c2 |
|
|||||||
|
|
|
se,i |
|
e,i m |
||||||
|
|
se |
|
|
si |
|
|
|
|
e,i |
|
Теперь уже не сложно найти интересующее нас решение:
|
|
ω2 |
|
|
ω2 = k 2c2 |
+ |
|
pi |
. |
|
ω2 |
|||
si |
|
|
|
|
|
|
1 + |
pe |
|
|
|
k 2 cse2 |
|
|
Учтем теперь, что по определению соответствующих величин имеет место соотношение:
173

c2 |
≡ |
γ |
|
T |
m |
≡ γ |
r2 . |
se |
|
e |
e |
e |
|||
ω2 |
|
4πe2 n |
m |
|
e De |
||
pe |
|
|
|
|
ei e |
|
|
Тогда полученный нами результат можно записать в виде
|
|
ω |
2 |
|
|
|
ω2 = k 2csi2 + |
|
|
|
pi |
. |
(4.51) |
1 + |
|
|
1 |
|||
|
|
|
|
|
||
|
γ |
e |
k 2r2 |
|
|
|
|
|
|
De |
|
|
|
Для коротких волн, когда длина волны меньше электронного дебаевского радиуса, знаменатель во втором слагаемом примерно равен единице, и мы получаем:
ω2 k 2c2 |
+ω2 |
≡ ω2 |
|
+ |
γiTi k 2 r2 |
|
k 2r2 |
<< 1 . |
(4.52) |
|
1 |
, |
|||||||||
si |
pi |
pi |
|
ZT |
De |
De |
|
|
||
|
|
|
|
|
e |
|
|
|
|
|
Частота этих волн оказывается порядка ионной ленгмюровской частоты. По аналогии с (4.46), эти волны называют ионными ленгмюровскими волнами. Как правило, если температура ионов не мала, они сильно затухают в плазме, так как оказываются резонансными по отношению к ионам.
В обратном пределе длинных волн, длина волны которых превышает электронный дебаевский радиус, в знаменателе второго слагаемого в формуле (4.51) главным, напротив, является второй член, и мы получаем:
ω2 |
k |
2c2 |
+ γ |
e |
k 2 r2 |
ω2 |
≡ k 2 c2 |
, |
k 2r2 |
<< 1 . |
(4.53) |
||
|
|
si |
|
|
De |
|
pi |
s |
|
De |
|
|
|
где обозначено |
|
|
|
|
|
|
ZγeTe +γiTi |
|
|
|
|||
c2 |
≡ c2 |
+γ |
r2 |
ω2 |
= |
. |
|
(4.54) |
|||||
|
|
||||||||||||
s |
si |
|
e De |
pi |
|
|
|
mi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сравнив (4.54) с точным результатом кинетической теории [18], заключаем, что в рассматриваемом диапазоне частот кинетика и гидродинамика, использованная нами, дают совпадающие
результаты при выборе |
γe = 1, γi = 3 , так |
что (4.54) |
||
следует записывать в виде: |
ZTe + 3Ti |
|
|
|
cs2 = |
. |
(4.55) |
||
|
||||
|
Mi |
|
||
174
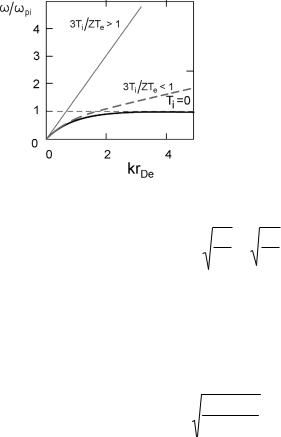
Рис. 4.4. Ионно-звуковые волны в плазме
Вытекающий из соотношения (4.53) закон дисперсии
ω = kcs , |
(4.56) |
согласно которому частота волны оказывается прямо пропорциональной волно-вому числу, типичен для звуковых волн (напомним, что мы обсуждаем сейчас продольные волны!)
Например, закон дисперсии звука в обычном газе
ω = kcs , cs = |
∂p |
= |
γT |
, |
|
∂ρ |
|
M |
|
где Т − температура, а М − масса молекул газа. По этой причине волны с законом дисперсии (4.55), (4.56) принято называть ионнозвуковыми волнами. Наряду с ленгмюровскими волнами, это важнейший тип способных распространяться в плазме волн (см.
рис.4.4).
Очевидно, фазовая и групповая скорости ионно-звуковой волны совпадают:
v |
= v |
= c |
s |
= ZTe +3Ti . |
(4.57) |
™ |
‹ р |
|
Mi |
|
|
|
|
|
|
|
Величина этих скоростей существенно зависит от соотношения температур компонент плазмы. При этом если
Ti ≥ Te ,
то фазовая скорость ионно-звуковой волны будет по величине порядка тепловой скорости ионов. Такие волны должны сильно поглощаться в плазме, так как они становятся резонансными по отношению к ионам. Поэтому ионно-звуковая волна может существовать только в сильно неизотермической плазме, когда электронная компонента сильно «перегрета» по отношению к
175
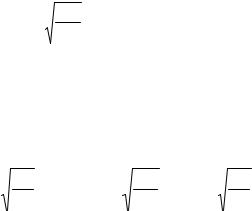
ионной. В этом случае вклад температуры ионов в формуле (4.57) является малым, и поэтому скорость ионно-звуковой волны главным образом определяется температурой электронов:
c |
s |
ZTe , |
T |
>> T . |
(4.58) |
|
Mi |
e |
i |
|
|
|
|
|
|
|
В этом случае, поскольку в формулу для скорости звука в качестве меры тепловой энергии входит электронная температура, а в качестве инерционного фактора входит масса ионов, принято эти волны называть «ионным звуком с электронной температурой».
Собирая вместе все указанные выше неравенства, получим область фазовых скоростей, в которой возможно существование ионнозвуковых волн:
v |
= |
3Ti << v |
~ c |
s |
|
ZTe << v |
= |
3Te . |
(4.59) |
Ti |
|
™ |
|
|
Te |
|
me |
|
|
|
|
Mi |
|
|
|
Mi |
|
|
Взяв теперь эти неравенства в качестве отправной точки, можно существенно упростить вывод закона дисперсии для ионного звука. Действительно, поскольку фазовая скорость волны предполагается малой по сравнению с тепловой скоростью электронов, инерция последних становится несущественной, по этой причине электронная подсистема может считаться квазиравновесной, а, следовательно, действующие в этой подсистеме силы − сила со стороны поля волны и сила, обусловленная градиентом электронного давления, − должны быть уравновешены. Поскольку продольная волна всегда
является потенциальной, введем потенциал поля волны согласно
E .
~r = −ϕ
Тогда баланс указанных сил, предполагая электронную температуру постоянной, можно записать так:
| e | ne ϕ −Te ne = 0 , |
(4.60) |
и, как мы видим, концентрация электронов определяется распределением потенциала поля волны. Можно сказать и так: «безынерционные» электроны мгновенно подстраиваются под профиль поля, создаваемый волной, скапливаясь в тех областях, где потенциал поля больше:
|
|
|
|e|ϕ |
|
|
n |
= n exp |
. |
|||
|
|||||
e |
e0 |
|
Te |
|
|
|
|
||||
Здесь ne0 - невозмущенная полем волны концентрация электронов (в области нулевого потенциала). Полученный результат, как мы видим, совпадает с
176
известной формулой Больцмана для равновесного распределения частиц, в нашем случае электронов, во внешнем поле.
Для ионной подсистемы плазмы ситуация противоположная. Поскольку фазовая скорость волны значительно превышает тепловую скорость ионов, можно пренебречь конечностью ионной температуры, считая ионы холодными, но принципиально учесть инерцию ионов, ограничивающую частоту колебаний. Для холодных Z-кратно ионизованных ионов уравнение движения выглядит так:
|
dvi |
= −Z | e | ϕ |
. |
(4.61) |
|
Mi dt |
|||||
|
|
||||
Под действием поля волны ионы плазмы приходят в движение, и их концентрация начинает изменяться, так как согласно уравнению непрерывности
∂ni |
+ div(ni vri ) = 0 . |
(4.62) |
∂t |
|
|
В качестве дополнительного условия, замыкающего систему (4.60) − (4.61), воспользуемся требованием квазинейтральности плазмы
ne = Zni , |
(4.63) |
которое, очевидно, должно выполняться, так как длина волны предполагается значительно превышающей электронный дебаевский радиус. В противоположном случае, когда волны короткие, условие (4.63) следует заменить уравнением Пуассона
Δϕ = 4π|e|(ne − Zni ).
Нелинейные уравнения (4.60) − (4.63) справедливы, в рамках высказанных выше предположений, для ионно-звуковых волн любой амплитуды. Ограничимся волнами малой амплитуды. Полагаем
~ |
~ |
r |
~ |
|
ϕ = ϕ |
|
r |
|
|
, ne,i = ne,i0 + ne,i , vi = vi |
, |
|||
где знаком тильда помечены малые возмущения. Подставим это представление в уравнения (4.60) − (4.63), разложим затем по амплитуде и, опустив нелинейные слагаемые, в результате получим
|
~ |
~ |
|
|
|e|ne0 ϕ − Te ne = 0 , |
|
|||
~r |
|
~ |
|
|
∂vi |
|
|
|
|
Mi ∂t |
= −Z | e | ϕ |
, |
(4.64) |
|
|
|
|
||
~ |
|
|
|
|
∂ni + div(ni0 vri ) = 0 , |
|
|||
∂t |
~ |
|
|
|
~ |
|
|
|
|
ne = Zni , ne0 = Zni0 . |
|
|||
Выразив теперь все величины через одну из них, например, через потенциал поля волны, получим волновое уравнение
177
∂ 2 ~ |
2 |
~ |
2 |
|
ZTe |
|
|
|
|
ϕ |
− cs |
ϕ |
= 0,cs |
= |
|
, |
(4.65) |
∂t2 |
Mi |
|||||||
следствием которого, как нетрудно проверить, является закон дисперсии (4.56), причем величина входящей в него скорости звука определяется формулой
(4.58).
Мы рассмотрели самые простые дисперсионные уравнения для незамагниченной плазмы. Для удобства читателей, наиболее важные из них сведены в табл. 4.1.
§ 33. Бесстолкновительное затухание волн в плазме
Выше при обсуждении конкретных типов волн, способных распространяться в плазме, мы неоднократно ссылались на резонансные эффекты, имеющие место, когда скорости частиц плазмы совпадают с фазовой скоростью волны. Здесь, не вдаваясь в подробности достаточно сложных математических выкладок (см. [20]), обсудим кратко физическую сторону механизма
бесстолкновительного затухания волн в плазме, впервые предсказанного Ландау. Когда говорят о резонансном взаимодействии волн и частиц плазмы, то, по сути дела, речь идет о черенковском резонансе
ω − kvr = 0 . |
(4.66) |
Фазовая скорость поперечной волны в изотропной плазме, как мы видели раньше, превышает скорость света. Следовательно, это условие заведомо не может выполняться и резонансные эффекты такого рода, как можно ожидать, будут несущественны. Имеет смысл поэтому рассмотреть резонансное взаимодействие частиц плазмы с продольными волнами, фазовая скорость которых существенно меньше скорости света, так что выполнение условия резонанса возможно. Пусть для простоты продольная волна будет одномерной (плоской). Обычно механизм бесстолкновительного поглощения энергии волн частицами плазмы поясняют с помощью следующей наглядной картинки, изображенной на рис. 4.5, идею которой мы заимствовали из книги [21].
178
|
|
|
|
|
|
|
|
|
|
Таблица 4.1 |
||||
|
|
|
|
|
|
|
|
|
|
|||||
Тип волны |
Закон дисперсии |
Фазовая |
|
Групповая |
Примечание |
|||||||||
|
|
|
|
|
|
|
скорость |
|
скорость |
|
|
|
|
|
Электронная |
|
ωLe |
|
ωLe k |
0 |
krDe → 0 |
||||||||
ленгмюровская |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
волна в холодной |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
плазме |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Электронная |
|
|
3 |
|
|
≈ ω |
k |
vTe (kvTe ωLe ) |
kr |
< 1 |
||||
ω |
1 + |
|
|
|
k 2r2 |
Le |
|
|
De |
< |
|
|||
ленгмюровская |
|
|
|
|
|
|
|
|
||||||
2 |
|
|
|
|
|
|
|
|
||||||
|
Le |
|
De |
|
|
|
|
|
|
|
|
|||
волна в «теплой» |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
плазме |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ионно-звуковая |
|
kcs |
|
cs |
|
cs |
c |
|
ZTe |
, |
||||
|
|
|
|
|
||||||||||
|
|
|
s |
|
|
mi |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
волна |
|
|
|
|
|
|
|
|
|
|
Te |
>> Ti |
||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
krDe << 1 |
||||
Поперечная |
|
ωLe2 |
+ k 2c2 |
c 1 + ωLe2 |
k 2 c2 |
c 1 + ωLe2 k 2c2 |
|
|
|
|
|
|||
плазменная волна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
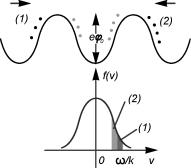
В движущейся системе координат, относительно которой волна покоится, наглядно можно ее представлять как последовательность горбов и ям потенциала. Частицы, скатывающиеся в ямы, ускоряются, а частицы, закатывающиеся на горбы, напротив, замедляются полем волны. Выделим, как показано на рис. 3.5, две
Рис. 4.5. К механизму резонансного поглощения волн в плазме. Вверху: «горбы и впадины» потенциала поля волны в системе ее покоя; стрелками показаны направления скоростей опережающих (1) и отстающих (2) групп частиц. Внизу: функция распределения частиц по скоростям в неподвижной системе координат. Выбранная волна бежит слева направо
группы частиц, отвечающих одному и тому же интервалу v справа (группа (1)) и слева (группа (2)) от скорости, совпадающей по величине и направлению с фазовой скоростью волны. В движущейся с фазовой скоростью системе координат первые, очевидно, обгоняют волну, а вторые отстают от нее (для наглядности изображено разное количество кружочков). Если в качестве таких групп частиц взять те, которые на рисунке условно изображены черными точками, то обе группы частиц тормозятся, так как их скорости в данный момент времени направлены к «горбам» потенциала, на которые поэтому они вынуждены забираться. Однако движущиеся направо при этом как бы «подталкивают» горб вперед, а движущиеся налево, напротив, «толкают» его назад. Если же в качестве таких групп частиц взять те, которые условно изображены светлыми точками, то поскольку при том же самом направлении скорости частицы обеих групп
180
