
Емелянов Лекции по основам електрослабой 2007
.pdfФедеральное агентство по образованию
МОСКОВСКИЙ ИНЖЕНЕРНО-ФИЗИЧЕСКИЙ ИНСТИТУТ (ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ)
В.М. Емельянов, К.М. Белоцкий
ЛЕКЦИИ ПО ОСНОВАМ ЭЛЕКТРОСЛАБОЙ МОДЕЛИ И НОВОЙ ФИЗИКЕ
Рекомендовано УМО «Ядерные физика и технологии»
в качестве учебного пособия для студентов высших учебных заведений
Москва 2007
УДК 539.1 (075) ББК 22.38я7 Е60
Емельянов В.М., Белоцкий К.М. Лекции по основам электрослабой модели и новой физике: Учебное пособие. – М.: МИФИ, 2007. – 236 с.
В данном пособии изложена электрослабая модель: ее предпосылки, основы и существующие проблемы. Описаны некоторые популярные варианты расширения электрослабой модели: модели суперсимметрии, «малого Хиггса», техницвета и модели с дополнительными измерениями. Показана связь рассмотренной физики с космологией.
Пособие рассчитано на студентов, специализирующихся по физике элементарных частиц, космомикрофизике.
Пособие подготовлено в рамках Инновационной образовательной программы.
Рецензент: канд. физ.-мат. наук, доцент А.В. Берков
ISBN 978-5-7262-0826-8
© Московский инженерно-физический институт (государственный университет), 2007
|
Редактор Е.Н. Кочубей |
|
|
|
|
Подписано в печать 10.11.2007. |
Формат 60×84 1/16 |
|
Объем 14,75 п.л. |
Уч. изд. л. 15,0. |
Тираж 200 экз. |
Изд. № 4/22. |
Заказ |
|
Московский инженерно-физический институт (государственный университет). 115409, Москва, Каширское шоссе, 31 Типография издательства «Тровант», г. Троицк Московской обл.
СОДЕРЖАНИЕ |
|
ПРЕДИСЛОВИЕ................................................................................... |
5 |
1. ФЕНОМЕНОЛОГИЧЕСКИЕ ОСНОВЫ |
|
ЭЛЕКТРОСЛАБОЙ МОДЕЛИ |
|
1.1. Введение.................................................................................. |
6 |
1.2. Токи. Структура слабых токов.............................................. |
6 |
1.3. Теория Ферми слабых взаимодействий................................ |
9 |
1.4. Нарушение четности и (V-A) форма заряженных |
|
слабых токов .......................................................................... |
9 |
1.5. (V-A) теория заряженных слабых взаимодействий ............ |
11 |
1.6. Теория промежуточного векторного бозона ....................... |
13 |
2.ПРИНЦИПЫ ПОСТРОЕНИЯ КАЛИБРОВОЧНЫХ ТЕОРИЙ
2.1. Симметрии и группы симметрий в физике.......................... |
15 |
2.2. Калибровочный принцип....................................................... |
18 |
2.3. Спонтанное нарушение симметрии...................................... |
25 |
2.4. Теорема Голдстоуна............................................................... |
29 |
2.5. Механизм Хиггса ................................................................... |
30 |
3. ЭЛЕКТРОСЛАБАЯ МОДЕЛЬ |
|
3.1. Введение.................................................................................. |
33 |
3.2. Правые и левые фермионы. ................................................... |
34 |
3.3. Выбор калибровочной группы. ............................................. |
35 |
3.4. Механизм Хиггса и массы W и Z .......................................... |
40 |
3.5. Общие свойства электрослабой модели............................... |
44 |
3.6. Лагранжиан электрослабой модели...................................... |
56 |
3.7. Предсказания электрослабой модели ................................... |
58 |
3.8. Хиггсовский бозон ................................................................. |
62 |
3.9. Стандартная модель ............................................................... |
69 |
4. НОВАЯ ФИЗИКА |
|
4.1. Суперсимметрия..................................................................... |
70 |
4.2. Альтернатива SUSY: «малый хиггс» (МХ) .......................... |
86 |
4.3. Внешние (дополнительные) измерения............................... |
97 |
4.4. Техницвет................................................................................ |
117 |
4.5. Расширенный техницвет (ETC)............................................. |
134 |
5. НОВАЯ ФИЗИКА В КОСМОЛОГИИ |
|
5.А. КОСМОЛОГИЧЕСКИЕ ОГРАНИЧЕНИЯ........................................ |
147 |
5.1. Введение.................................................................................. |
147 |
5.2. Фридмановская модель Горячей Вселенной........................ |
148 |
3
5.3. Предсказательная сила космологии: ограничения |
|
на физику ранней Вселенной ................................................ |
160 |
5.4. Примеры космологических ограничений |
|
конкретных физических моделей ......................................... |
174 |
5.Б. КОСМОЛОГИЧЕСКИЕ СВИДЕТЕЛЬСТВА НОВОЙ |
|
ФИЗИКИ ................................................................................................ |
181 |
5.5. Проблемы «старой» космологии........................................... |
181 |
5.6. Новая физика как решение проблем «старой» |
|
космологии.............................................................................. |
192 |
ПРИЛОЖЕНИЕ |
|
П.1. Основы физики нейтрино ..................................................... |
217 |
П.2. CP-четность и ее нарушения ................................................ |
224 |
П.3. Сильное CP-нарушение и модель аксиона.......................... |
228 |
П.4. CPT-теорема........................................................................... |
234 |
СПИСОК ЛИТЕРАТУРЫ.................................................................... |
236 |
4
ПРЕДИСЛОВИЕ
В 2008 г. в ЦЕРН начнет свою работу крупнейший ускоритель протонов – Большой адронный коллайдер. Его задачами являются: 1) проверка современной модели элементарных частиц и их взаимодействий – стандартной модели; 2) поиск новой физики вне рамок стандартной модели. Как ожидается, будет проверен механизм нарушения электрослабой симметрии и обнаружен бозон Хиггса. Эта частица оказывается «последним кирпичиком» при построении стандартной модели. Обнаружение (как и не обнаружение) бозона Хиггса ставит перед современной физикой высоких энергий новые проблемы, для разрешения которых необходима «новая» физика (суперсимметрия, техницвет, дополнительные измерения и т.д.). Если «новая» физика существует (а в этом мало кто из физиков сомневается), то она должна себя проявлять и в космологии.
Предлагаемая книга основана на курсе лекций, читаемых для студентов 4-го и 5-го курсов факультета экспериментальной и теоретической физики МИФИ. Глава 1 содержит феноменологические основы электрослабой модели. В главе 2 сформулированы калибровочный принцип построения калибровочных теорий, рассмотрены идеи спонтанного нарушения симметрии и механизм Хиггса. В главе 3 обсуждается электрослабая модель и ее предсказания. В главе 4 рассмотрены некоторые из возможностей для «новой» физики (суперсимметрия, техницвет, малый Хиггс, дополнительные измерения). Глава 5 содержит обсуждение проявлений «новой» физики в космологии.
Авторы выражают благодарность М.Ю. Хлопову и А.В. Беркову за полезные обсуждения и рекомендации, а также К.И. Шибаеву за помощь в подготовке рукописи.
5
1. ФЕНОМЕНОЛОГИЧЕСКИЕ ОСНОВЫ ЭЛЕКТРОСЛАБОЙ МОДЕЛИ
1.1. Введение
Существование слабых взаимодействий было постулировано для объяснения экспериментальных данных по временам жизни нейтрона, p-, m-мезонов:
n ® pe− νe , |
τn = 920 с, |
(1.1а) |
|||
π− ® µ− νµ , |
τπ− |
= 2,6 ×10−8 с, |
(1.1б) |
||
µ− ® e− |
|
e νµ , |
τµ− |
= 2, 2 ×10−6 с. |
(1.1в) |
ν |
|||||
Эти времена гораздо больше времен жизни частиц, распадающихся по сильным и электрослабым взаимодействиям:
→ pπ , |
τπ− |
=10−23 с, |
(1.2а) |
||
π0 ® γγ , |
τ |
π |
0 |
=10−16 с. |
(1.2б) |
|
|
|
|
|
|
Вообще история развития представлений о слабых взаимодействиях до создания электрослабой модели представляет собой интересный пример взаимосвязи теории и эксперимента. В свое время существовало множество феноменологических моделей, которые проверялись и опровергались при сравнении с экспериментальными данными. Среди этих теорий следует отметить теорию Ферми, (V-A) теорию Фейнмана и Гелл-Манна, а также теорию IVB (промежуточного векторного бозона) Ли, Янга и Глэшоу. Обсудим основные идеи предшественников электрослабой модели.
1.2. Токи. Структура слабых токов
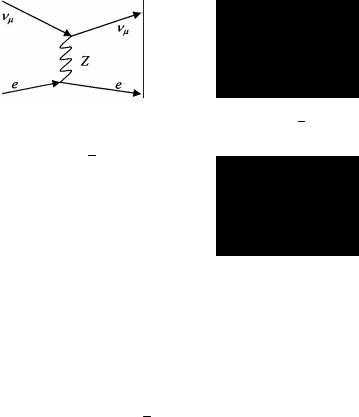
Электромагнитное взаимодействие можно описать как взаимодействие электромагнитного тока с фотонами. Например, упругое рассеяние ee → ee (рис.1.1) описывается взаимодействием двух электромагнитных токов с g-квантом.
6
Аналогично электромагнитному, слабое взаимодействие можно рассматривать как взаимодействие слабого тока с промежуточным
W ± - и Z 0 -бозонами. Слабые токи, связанные с испусканием и по-
глощением W ± , называются заряженными токами, так как они изменяют электрические заряды входящих в них частиц. Пример таких токов приведен на рис.1.2.
Рис. 1.1. Диаграмма процесса ee→ee
С Z 0 -бозонами связаны нейтральные токи типа ee , νµ νµ , µµ и
т.д., когда входящие и выходящие частицы в вершину взаимодействия одинаковые. С нейтральными токами связано, например, рассеяние νµe → νµe (рис.1.3).
Заряженные и нейтральные слабые токи содержат лептонную
Рис. 1.2. Диаграмма процесса µ− → e− νe νµ
Рис. 1.3. Диаграмма процесса eν→eν
и адронную части. Для трех поколений лептонов
νe |
νµ |
ντ |
|
|||||
|
− |
|
µ |
− |
|
τ |
− |
(1.3) |
e |
|
|
|
|
|
|
||
у каждого заряженного лептона есть свое нейтрино. Заряженный
лептонный ток je образует лептон со своим нейтрино: |
|
je = eνe + µνµ + τντ . |
(1.4) |
Очевидно, что при этом испускаются W+-бозоны или поглощаются W– -бозоны. Эрмитово-сопряженный ток
j |
+ = |
|
|
e + |
|
|
µ + |
|
|
τ |
(1.5) |
ν |
e |
ν |
ν |
τ |
|||||||
|
e |
|
µ |
|
|
|
|
||||
содержит испускание W − -бозонов или поглощение W + -бозонов.
7
Нейтральный лептонный ток je0 включает шесть слагаемых: νe νe , νμνμ , ντντ , ee , μμ , ττ . Лептонные токи описывают процес-
сы как с участием лептонов, так и с участием антилептонов ( e + ,
μ+ , τ+ , νe , νμ , ντ ).
Как известно, адроны участвуют в слабых взаимодействиях. Рассмотрим это взаимодействие на кварковом уровне. Сейчас известно, как и в случае лептонов, три семейства кварков:
u |
c |
t |
(1.6) |
|
|
|
|
. |
|
d |
s |
b |
|
|
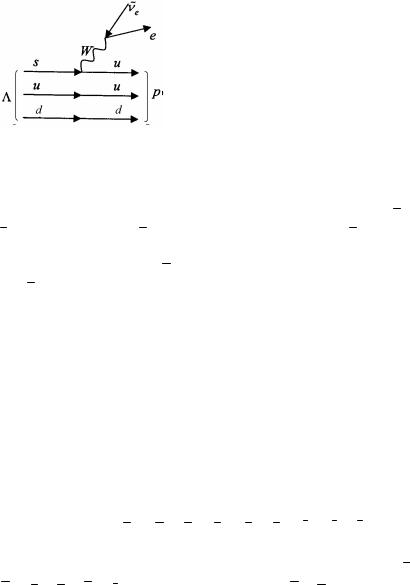
Наиболее хорошо изучены слабые превращения кварков первых двух семейств. В заряженный ток кварки входят не только со своими партнерами, но и с «чужими». Например, наряду с токами ud и cs существует и ток us . В самом деле, если бы тока us не было, то странные частицы были бы абсолютно стабильными, а они распадаются. Например, ток ud определяет распад нейтрона (рис.1.4). Ток us входит в диаграмму распада Λ-гиперона (рис.1.5).
|
|
|
|
|
|
Рис. 1.5. Диаграмма распада |
|
Рис. 1.4. Диаграмма распада |
|||
|
Λ-гиперона |
||
нейтрона |
|
Если каждый «верхний» кварк может переходить в каждый из «нижних» кварков, то заряженный адронный ток будет содержать девять слагаемых: ud , us , ub , cd , cs , cb , t d , ts , t b . Девять компонент содержатся и в эрмитово-сопряженном токе.
Нейтральный адронный ток j0h имеет шесть компонент: uu ,
dd , ss , cc , b b , t t . Нейтральные токи типа ds , uc (горизонтальные превращения) отсутствуют.
8

Следует заметить, что кварки несут цветовые степени свободы. Поскольку цветовая симметрия не нарушена, то слабые кварковые токи, как и адроны, являются бесцветными. Поэтому, например, ток ud представляет собой сумму трех слагаемых:
|
|
d = |
|
i d |
|
= |
|
1d + |
|
2d |
|
+ |
|
3d |
|
. |
(1.7) |
u |
u |
i |
u |
u |
2 |
u |
3 |
||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||
Суммирование ведется по цветовым индексам.
1.3.Теория Ферми слабых взаимодействий
В1934 г. для описания b-распада нейтрона n ® pe− ne Э.Ферми предложил 4-фермионную теорию, лагранжиан которой
LF |
= - |
G |
F |
|
( |
|
(x)γλn(x))( |
|
(x)γλ νe (x)) + э.с. |
(1.8) |
|
p |
e |
||||||||
|
|
|
||||||||
|
||||||||||
|
2 |
|
|
|
|
|
|
|
||
Этот лагранжиан выглядит как произведение двух токов – адронного и лептонного с векторным взаимодействием в вершине.
Величина GF =1,166 ×10−5 ГэВ-2 – размерная фермиевская константа слабых взаимодействий. Лагранжиан LF подразумевает локальный
характер четырехфермионных взаимодействий: два тока взаимодействуют в одной пространственно-временной точке x.
Следует отметить, что из-за векторной структуры слабых токов в теории Ферми эта теория не объясняет наблюдаемое экспериментально нарушение четности в слабых взаимодействиях.
1.4. Нарушение четности и (V-A) форма заряженных слабых токов
Наблюдение распадов каонов на состояния с противоположны-
ми четностями: K + ® p+ p0 и K + ® p+ p+ p− привело в 1956 г. Ли и Янга к предположению о несохранении четности в слабых взаимодействиях, «ответственных» за эти распады. Нарушение четности открыто в 1957 г. (мадам Ву и коллабораторы) при анализе b-
распада ядра кобальта 60 Co ® 60 Ni e− νe , происходящего при рас-
паде нейтрона n ® pe− ne . Ядра поляризовались внешним магнитным полем таким образом, чтобы угловые моменты Co и Ni,
9
равные J = 5 и J = 4 соответственно, были выстроены в направлении внешнего поля. При сохранении углового момента угловой
момент системы электрон– антинейтрино должен быть J (e− ne ) =1
и выстроен так же, как другие моменты. Поэтому спины электрона и антинейтрино (это фермионы) должны быть выстроены в том же направлении. Электрон от распада всегда наблюдается движущимся в направлении, противоположном внешнему полю. По закону сохранения импульса недетектируемое антинейтрино должно двигаться в направлении, противоположном направлению движения электрона. Это означает, что рожденный электрон имеет отрицательную спиральность (левую), а антинейтрино – положительную спиральность (правую). Напомним, что фермионное поле можно представить в виде
|
|
Y = YL + YR , |
(1.9) |
|||||
YL |
= |
1 - g5 |
Y , |
YR |
= |
1 + g5 |
Y . |
(1.10) |
|
||||||||
|
|
|||||||
|
2 |
|
|
2 |
|
|
||
Таким образом, заряженные слабые токи, связанные с этим распадом, всегда порождаются левыми компонентами электронов и правыми компонентами антинейтрино. Ненаблюдение левых антинейтрино, а также правых нейтрино в заряженных слабых токах является сигналом нарушения четности, поскольку преобразование четности меняет левые фермионы на правые фермионы.
Как оказалось, слабый заряженный ток имеет «векторную минус аксиально-векторную форму»
Jμ ~ Vμ - Aμ . |
(1.11) |
Векторный и аксиально-векторный токи при преобразовании четности (P) трансформируются следующим образом:
P |
|
|
+yg |
y; |
||
|
|
|||||
V μ = ygμy ¾¾® |
|
0 |
|
|
||
|
|
|
(1.12а) |
|||
|
|
-ygk y, k =1, 2,3; |
||||
|
|
|
|
|
|
|
5 P |
|
-yg |
g |
|
y; |
|
|
5 |
|||||
Aμ = ygμ g y ¾¾® |
|
0 |
|
|
||
|
|
|
|
(1.12б) |
||
|
+ygk g5y, k =1, 2,3. |
|||||
|
|
|
|
|
|
|
Соответственно, произведения токов при P-преобразовании изменяются так:
10
