
Емелянов Фундаменталные симметрии 2008
.pdf
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
МОСКОВСКИЙ ИНЖЕНЕРНО-ФИЗИЧЕСКИЙ ИНСТИТУТ (ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ)
В.М. Емельянов
ФУНДАМЕНТАЛЬНЫЕ
СИММЕТРИИ
Рекомендовано УМО «Ядерные физика и технологии»
в качестве учебного пособия для студентов высших учебных заведений
Москва 2008

УДК 539.12(075) ББК 22.38я7 Е 60
Емельянов В.М. Фундаментальные симметрии: Учебное посо-
бие. М.: МИФИ, 2008. – 560 с.
Данное пособие посвящено подробному обзору современного положения в физике элементарных частиц. Эта книга может быть полезна как студентам высших курсов технических вузов, так и научным сотрудникам технических институтов.
Пособие подготовлено и реализовано в рамках Инновационной образовательной программы МИФИ.
Рецензент д-р физ.-мат. наук С.Г. Рубин
ISBN 978–5–7262–1040–7
© Московский инженерно-физический институт (государственный университет), 2008
Редактор Т.В. Волвенкова
Оригинал-макет изготовлен С.В. Тялиной
Подписано в печать 05.09.2008. Формат 60×84 1/16. Уч.-изд. л. 34,5. Печ. л. 35,0. Тираж 150 экз. Изд. № 4/57. Заказ №
Московский инженерно-физический институт (государственный университет). 115409, Москва, Каширское ш., 31
Типография издательства «Тровант», г. Троицк Московской области

Емельянов Валерий Михайлович
К величайшему прискорбию Валерий Михайлович Емельянов не застал выхода в свет этой книги. Его жизнь оборвалась 4 июля 2008 года. Это был выдающийся педагог и ученый. Его энергия и педагогический талант способствовали воспитанию большого числа высококвалифицированных специалистов МИФИ. Достойной памятью о нем будет продолжение им начатых дел его учениками.
Предисловие |
Посвящаю своим родителям |
История физики содержит множество примеров, показывающих важность симметрийного подхода к анализу экспериментальных данных и развитию новых представлений. Например, загадочные свойства атомов в периодической системе элементов выглядят естественно при рассмотрении их вращательной симметрии. Другой пример – теория относительности становится весьма элегантной, если её сформулировать «из первых принципов» и воспользоваться лоренц-инвариантностью. Каждая частица определяется набором квантовых чисел. Эти числа характеризуют «внутренние» состояния частицы. Их называют «внутренними», чтобы подчеркнуть, что они не имеют отношения к кинетическим состояниям частицы, характеризуемым законами сохранения энергии, импульса и углового момента.
Существование квантового числа в системе всегда возникает вследствие инвариантности системы относительно глобального преобразования, не зависящего от координат пространственновременной точки, где оно было произведено. Существуют три типа симметрий.
1.Непрерывные симметрии пространства-времени. Согласно теореме Нетер, каждая непрерывная симметрия приводит к сохраняющемуся току. Соответствующие этим симметриям квантовые числа аддитивны, т.е. квантовое число, связанное с заданной симметрией составной системы, получается путем сложения (алгебраического или векторного) квантовых чисел компонент системы.
2.Дискретные симметрии. В этом случае квантовые числа мультипликативны – квантовое число составной системы задается произведением квантовых чисел всех составляющих системы.
3.Унитарные симметрии. С ними связаны фазовые преобразования полей во «внутреннем» пространстве. Таким преобразованиям симметрии соответствует сохранение обобщенного заряда (электрический заряд, барионное, лептонное число и т.д.). Квантовые числа преобразований унитарной симметрии аддитивны.
Любое непрерывное преобразование симметрии можно сделать локальным, т.е. зависящим от координат той пространственновременной точки, в которой это преобразование проводится. Симметрии, соответствующие преобразованиям такого типа, называются локальными (калибровочными) симметриями.
5
Очевидно, что точная симметрия очень важна в физике частиц. Она позволяет определить новую частицу в реакции, в которой все другие частицы уже имеют известный набор квантовых чисел. В силу теоремы Нетер, симметрии динамической системы и сохраняющиеся величины оказываются взаимосвязанными. Этот результат широко используется при построении моделей элементарных частиц.
Следует подчеркнуть, что многие симметрии в физике частиц не являются точными симметриями. Говорят, что симметрия нарушена, если некоторая величина, обычно ненаблюдаемая вследствие симметрии, при определенных условиях становится наблюдаемой. Может показаться, что изучение нарушенных симметрий непродуктивно. Но это не так. Во-первых, природа устроена так, что многие симметрии нарушаются. Во-вторых, это нарушение происходит достаточно упорядоченно, и это опять-таки можно использовать при построении моделей элементарных частиц и их взаимодействий.
Среди симметрий особую роль играют фундаментальные симметрии. Они связаны с наиболее общими принципами построения современных теорий элементарных частиц. К таким принципам относится принцип общей ковариантности, выраженный инвариантностью относительно преобразований диффеоморфизмов в общей теории относительности, и принцип эквивалентности любых локальных систем отсчёта, связанный с локальными преобразованиями Лоренца. Эти хорошо известные пространственновременные симметрии описывают наблюдаемый мир от астрономических масштабов до расстояний ~ 10–18 м. Остаются ли эти симметрии “хорошо работающими” на меньших масштабах. Как ожидается, много новой информации на эту тему будет получено уже достаточно скоро – после начала работы Большого адронного коллайдера ЦЕРН, который заработает в 2008 году.
Эти эксперименты, как мы надеемся, окажутся чрезвычайно важными для установления “внутренних” симметрий элементарных частиц и их взаимодействий.
Как хорошо известно, сохранение электрического заряда в электродинамике связано с инвариантностью этой теории относительно фазовых преобразований, т.е. с U(1) симметрией. Открытие Гейзенбергом изоспина нуклона привело к SU(2)F-симметрии (F характеризует аромат). Как оказалось, эта симметрия приближённая, на-
6
рушенная электромагнитным взаимодействием. После открытия странных частиц возникла SU(3)F симметрия Гелл-Манна и Неймана. В настоящее время основой понимания взаимодействий элементарных частиц является стандартная модель сильных и электрослабых взаимодействий, основанная на SU(3)c×SU(2)L×U(1)Y группе симметрии.
Достаточно очевидно, что стандартная модель не является “окончательной теорией”. Это утверждение следует как из “внутренних” проблем этой теории, рассмотренных в книге, так и её невозможности описать уже наблюдаемые данные. Речь, прежде всего, идёт о существовании тёмной материи. Эта материя состоит из частиц, не входящих в стандартную модель. С частицами стандартной модели они взаимодействуют лишь посредством гравитации. Стандартную модель следует считать, по-видимому, эффективной квантовой теорией поля, имеющей ограниченную область применимости. Необходимо предполагать существование более общей теории с расширенным составом частиц, новыми взаимодействиями и новыми симметриями. Возможностей, некоторые из которых рассмотрены в книге, здесь чрезвычайно много. Какую (какие?) из них выбрала Природа? Может быть, результаты БАК укажут на “правильные” направления.
Книга организована следующим образом. Во введении приведена классификация пространственно-временных и внутренних симметрий. Лоренцевская и конформная симметрии рассмотрены в главе 1. Обсуждаются представления группы Лоренца, описываются релятивистские состояния массивных и безмассовых частиц. Если происходит спонтанное нарушение лоренцевской симметрии (СНЛС), и при этом все лоренц-неинвариантные эффекты, вызванные СНЛС, являются ненаблюдаемыми, то из этого базисного принципа можно получить калибровочно-инвариантные теории (абелевы и неабелевы), стартуя с произвольного релятивистскиинвариантного лагранжиана.
Глава 2 содержит доказательство CPT-теоремы, принадлежащее Иосту и основанное на функциях Вайтмана – аналитических продолжениях вакуумных матричных элементов от произведения полей. Показано, что фундаментальность CPT обусловлена её связью с лоренц-инвариантностью. Глава 3 посвящена симметриям стандартной модели. Рассмотрены как симметрии квантовой хромодинамики, так и симметрии электрослабого сектора. Точные и нару-
7
шенные симметрии в физике частиц составляют предмет изучения главы 4. В этой главе рассмотрены вигнер-вейлевская и намбуголдстоуновская реализации симметрии, а также теорема Голдстоуна и механизм Хиггса. Глава 5 посвящена изучению глобальных симметрий стандартной модели. Рассмотрены киральные аномалии, проблемы θ-вакуума, сильная CP-проблема и её киральное решение. Обсуждаются вопросы существования реальных намбуголдстоуновских бозонов и влияние гравитации на глобальные симметрии. В главе 6 обсуждаются дискретные симметрии (пространственная инверсия P, зарядовое сопряжение C, обращение времени T), а также их комбинации. Приведены наблюдаемые следствия нарушения дискретных симметрий.
Суперсимметрия и супергравитация обсуждаются в главе 7. Показано, что SUSY – один из способов разрешения проблемы иерархий стандартной модели. В этой главе рассмотрены теоретические основы суперсимметрии, спиноры и их свойства по отношению к преобразованиям Лоренца. Построен простейший суперсимметричный лагранжиан и минимальная суперсимметричная стандартная модель. Рассмотрены общие свойства теорий супергравитации в 4-х измерениях. Глава 8 посвящена симметриям Большого объединения. Обсуждаются группы симметрии SU(5), SO(10), E6, SU(5)×SU(5), SU(6), а также их суперсимметричные версии.
Механизмы нарушения фундаментальных симметрий – лоренцевской и CPT – рассматриваются в главе 9. В главе 10 обсуждаются проверки лоренц и CPT – инвариантности в физике высоких энергий, астрофизике и космологии. Проблемы CP-нарушения и возможные пути её разрешения рассматриваются в главе 11. Наконец, в главе 12 содержится обсуждение фундаментальных констант и их связей с фундаментальными симметриями.
Предлагаемая книга является продолжением предыдущей работы автора “Стандартная модель и её расширения”, знакомство с которой рекомендуется читателю.
Выражаю глубокую признательность Б.А. Долгошеину и А.А. Петрухину за интерес к работе и поддержку. Благодарю К.И. Шибаева, А.А. Кириллова и Е.Ю. Солдатова за помощь в подготовке рукописи.
Москва-CERN, Июнь 2008.
В. Емельянов
8
Введение
В повседневной жизни под симметрией обычно понимают симметрию между левым и правым (зеркальная симметрия). Для объекта в плоскости это означает существование линии симметрии; а для объекта в пространстве – плоскости симметрии. Если заменить одну часть объекта на другую, он будет выглядеть совершенно одинаково. Пожалуй, это первая симметрия, с которой мы встречаемся в повседневной жизни. Есть ли какие либо причины для появления подобной симметрии у человека и животных? Очевидно, существуют два выделенных направления: направление движения и направление силы тяготения. Вместе эти два направления образуют плоскость в пространстве. Что можно узнать, исследуя отражения? Симметрии обычно отражают некоторые внутренние свойства или характеристики объектов, а также того пространства, к которому принадлежат эти объекты. Легко заметить, что симметрии в природе часто реализованы приближенно, т.е. симметрии бывают нарушенными.
Остановимся на примере кустарников и деревьев. В этом случае есть только одно выделенное направление, задаваемое гравитацией, все горизонтальные направления одинаково хорошо приспособлены для поглощения света, углекислого газа и т.д. Следовательно, деревья и кустарники имеют одну ось симметрии, т.е. обладают вращательной симметрией. Деревья со многими ветками приближенно имеют непрерывную вращательную симметрию относительно вертикальной оси, цветы же обладают дискретной вращательной симметрией. Действительно, многие цветы характеризуются дискретной вращательной симметрией 5-го порядка: они преобразуют-
ся сами в себя при повороте на угол n5 360° (n z) относительно
оси симметрии. Интересно отметить, что модели роста цветка указывают на симметрию n 360°/k, где k – число Фибоначчи (1, 2, 3, 5, 8, 13…).
Что мы понимаем под симметрией?
Грубо говоря, объект называется симметричным (обладает симметрией) если существуют такие его преобразования, при заверше-
9
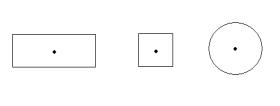
нии которых объект выглядит точно так же. Другими словами, преобразование симметрии геометрического объекта (являющегося частью плоскости или пространства) – это преобразование, которое невозможно детектировать. Например, для следующих геометрических фигур невозможно обнаружить эффект вращения относительно их осей симметрии на углы 180° , 90° и на произвольный угол.
Чем больше симметрий присуще объекту, тем более он симметричен.
Чтобы сформулировать точнее определение симметрии, напомним, что изометрией геометрического объекта в евклидовом пространстве называется преобразование, которое сохраняет все расстояния. Примерами изометрий являются вращения, сдвиги и отражения.
Симметрией или преобразованием симметрии геометрического объекта в евклидовом пространстве называется изометрия, которая отображает объект в самого себя. Если объект допускает определенную симметрию, то говорят, что он обладает инвариантностью относительно преобразований этой симметрии.
Набор всех преобразований симметрии может образовать группу. В этом случае говорят о группе симметрии объекта.
Симметрии законов природы
Симметрия закона природы означает, что мы можем определенным образом преобразовывать этот закон, но при этом мы не встречаемся с какими-либо наблюдаемыми изменениями. Более точно, рассмотрим физическую систему, описываемую некоторыми уравнениями, содержащими набор переменных, зависящих от пространственно-временных координат. Например, рассматривается распространение импульса со скоростью света с, описываемое
10
