Емелянов Фундаменталные симметрии 2008

Добавил:

fench Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский ядерный университет (МИФИ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ν = n+ − n− =

xGa Gaμν .

.pdf

Скачиваний:

109

Добавлен:

16.08.2013

Размер:

11.16 Mб

Скачать

☆

<<< < Предыдущая 7 8 9 10 11 12 13 14 15 16 17 1819 / 5619 20 21 22 23 24 25 26 27 28 29 30 31 > Следующая >>>

скольку существует очень строгое экспериментальное ограничение на нарушение барионного числа. например, для В – нарушающего

распада p → e+π0 ограничение

τ( p → e+π0 ) ≥ 5.5 1032 лет.

(5.38)

Чтобы понять, почему аномальный вклад в соотношение (5.36), связанный с U (1) A током важен, а аномальный вклад в (5.34), свя-

занный с (B+L) током, несущественен, необходимо исследовать свойства вакуума калибровочной теории.

5.3. Калибровочная теория вакуума

Вакуумное состояние, по определению, это такое состояние, в котором все поля обращаются в ноль. Для калибровочных полей это определение следует несколько расширить, поскольку эти поля сами по себе нефизические. Поэтому для калибровочных полей ва-

куумное состояние, в котором или Aaμ = 0 или состояние, получен-

ное калибровочным преобразованием Aaμ = 0 . Для этих целей дос-

таточно исследовать SU(2) калибровочную теорию, поскольку этот пример сохраняет черты более общих теорий.

В SU(2) теории удобнее рассматривать временную калибровку, в которой Aa0 = 0 (а= 1, 2, 3). В этой калибровке пространственные компоненты калибровочных полей оказываются независящими от времени Ai (rG,t) = Aai (rG) . Но даже в такой калибровке существует «остаточный» калибровочный «произвол». Определяя калибровочную матрицу Ai (rG) , свертывая калибровочные поля с матрицами

Паули Ai (rG,t) = τ2a Aai (rG) в Aa0 = 0 калибровке, мы сохраняем воз-

можность осуществления следующих калибровочных преобразований

G G

−1

(r ) → Ω(r )A

(r )Ω(r )

Ω(r )

(5.39)

181

где g – калибровочная константа SU(2) теории. Таким образом, в

A0	= 0 калибровке калибровочные поля, соответствующие вакуум-
a						Ω(rG)V iΩ(rG)−1 . Поведе-
ной конфигурации, образуют набор 0,					i
ной конфигурации, образуют набор 0,					g
	Ω(rG) при	r			g
ние			→ ∞определяет различные классы калибровоч-
ние			→ ∞определяет различные классы калибровоч-
ных полей. В частности, требование
			G	r→∞		(5.40)
			Ω(r ) →1			(5.40)

определяет отображение физического пространства [S3 ] на групповое пространство [SU(2) ~ S3]. Отображение S3 →S3 разделяет матрицы Ω(rG) на различные гомотопические классы {Ω(r )} , характеризующиеся целым числом («winding number»), которое опреде-

ляемым характером стремления Ω(r )		к единице на пространствен-
ной бесконечности
G	r→∞		2πin	.	(5.41)
Ωn (r ) →e

Тогда набор калибровочных полей, характеризующий вакуумное

состояние – {0, Ai

(rG)}, где

Ai (rG) =

(rG)V i Ω

(rG)−1 .

(5.42)

Winding number n – это якобиан S3 → S3

преобразования, и его

можно выразить следующим образом:

ig3

∫d

3 G

n =

rtr(εijk An

(r )An

(r )).

(5.43)

24π2

При этом можно построить

матрицу

преобразований

Ωn (r ) с

winding number n, объединяя n раз матрицу преобразований Ω1(r ) :
Ω	n	(rG) =[Ω (rG)]n .	(5.44)
	n	1

Для n = 1 матрица так называемого большого калибровочного преобразования имеет вид

	G	rG2 − λ2				2iλτG rG
Ω1	(r ) =	G2	+ λ	2	+	G2	+ λ	2	,	(5.45)
		r	+ λ			r	+ λ

где λ – произвольный масштабный параметр.

182

Если иметь в виду вышеупомянутые свойства, то становится очевидным, что n-е вакуумное состояние, соответствующее калиб-

ровочной конфигурации Ani (rG) , не является полностью калибровочно инвариантным. Действительно, большое калибровочное преобразование способно трансформировать Ani (rG) в следующее со-

стояние

Ai + (rG)

n 1

иначе говоря

= Ω1(rG)Ani (rG)Ω1(rG)−1 + gi Ω1(rG)V iΩ1(rG)−1,

Ω1 n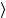 = n +1 .

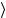(5.46)

(5.47)

Истинное вакуумное состояние калибровочной теории должно быть калибровочно-инвариантным, т.е. линейной суперпозицией n-вакуумных состояний. Это так называемый θ-вакуум (Поляков, Т’ Хоофт)

θ = ∑ e−inθ

n .

(5.48)

Поскольку

Ω1

θ = ∑e−inθΩ1

=∑e−inθ

n +1

= eiθ

θ ,

(5.49)

то θ-вакуум калибровочно-инвариантен.

использованием

θ-вакуума, как истинного вакуума калибровочных теорий, вакуумный функционал этих теорий делится на два различных сектора.

Если		θ ± − θ -вакуумные		состояния при		t = ±∞ , то		вакуумный


функционал теории принимает следующую форму:

+	θ		θ _ = ∑eimθe−inθ +	m	n _ = ∑eiνθ	∑ + n + ν	n	_ .	(5.50)
			n,m		ν	n

Таким образом, вакуумный функционал представляет собой сумму вакуумных амплитуд, у которых winding number при t = ±∞ отли-

чается на ν, взвешенных с фактором eiνθ . Можно ожидать, что су-

перпозиция амплитуд с различными фазами eiνθ приведет к СР нарушающим эффектам. Вспоминая, что вакуумный функционал,

183

задается интегралом по путям конфигураций калибровочного поля, взвешенным с классическим действием, получаем формулу

+ θ

θ _ =

∫ δAμeiS[ A] = ∑eiνθ

∑ +

n + ν

n _

(5.51)

пути

Хотя формула для

+ θ

θ _

получена в A0

калибровке,

параметр ν

имеет калибровочно-инвариантное значение. Согласно Полякову – Т’ Хоофту,

Чтобы это показать, следует воспользоваться тождеством Бардина, выражающим произведение GG через полную производную

GμνG μν = ∂μK μ . a a

где «ток » K μ задается соотношением

K μ = εμαβγ Aaα[Gaβγ − g3 εabc Abρ Acγ ] .

Для чисто калибровочных полей (Gaβγ = 0) в калибровке этот ток имеет только временную компоненту

K i = 0; K 0 = − g3 εijk εabc Aai Abj Ack = 34 igεijk tr(Ai A0 Ak ) .

(5.53)

(5.54)

Aa0 = 0

(5.55)

Используя эти соотношения, в этой калибровке для winding чисел n± получаем

n± =

ig3

d 3rεijk tr(Ai A j Ak ) =

g 2

d 3r K 0

(5.56)

24π2

∫

32π2 ∫

t=±∞

Эта формула позволяет выразить разность ν = n+ − n−

следующим

образом:

g 2

ν = n+ − n− =

d 3r K 0

t=+∞

dσμK μ.

(5.57)

32π2 ∫

t=−∞

Тогда соотношение (5.52) следует из теоремы Гаусса и тождества Бардина.

184

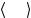
Если ν выражено через интеграл от GG , то можно переписать формулу для вакуумного функционала в терминах эффективного действия. Определяя

g 2

μν

Seff [A] = S[A] + θ

xGa

Gaμν ,

32π2 ∫

видим, что

g 2

θ _ = ∑

[ A]

+ θ

∫

δAμe

eff

δ ν −

32π

∫d 4 xGaμνGaμν .

пути

(5.58)

(5.59)

С учетом θ-вакуумной структуры, к лагранжиану калибровочной теории добавляется дополнительный член

			g 2		μν
L	= L	+ θ		G	a	G	aμν	.	(5.60)
			32π2
эф	калибр
Теория возмущений	связана		с ν = 0				сектором,		поскольку

∫d 4 xGG = 0 . Эффекты ν ≠ 0 включает непертурбативные процессы.

В качестве примера обратимся сначала к КХД. Предполагая существование n f ароматов, чьими массами можно пренебречь

(m f = 0) , запишем аксиальный ток


			1	n f
		J5μ =	1	∑qi γμγ5qi .						(5.61)
		J5μ =		∑qi γμγ5qi .						(5.61)
			2 i=1
Этот ток не сохраняется, и это следствие киральной аномалии
		μ			g32			μν
∂μJ5 = n f							Ga Gaμν .			(5.62)
∂μJ5 = n f					32π2		Ga Gaμν .			(5.62)
С точки зрения предыдущего рассмотрения, изменение										Q5 можно
связать с ν						g32
Q5 = ∫d	4	μ				g32			μν
		x∂μJ5	= n f						Ga Gaμν = n f ν.	(5.63)
		x∂μJ5	= n f			32π2			Ga Gaμν = n f ν.	(5.63)

Очевидно, если сектора ν ≠ 0 важны для KXД, то изменение (5.63) означает, что U(1)А симметрия не является симметрией теории. Отсюда следует физическое объяснение тому (для nf = 2), что η не имеет свойств голдстоуновского бозона.

185

Т’ Хоофт, используя квазиклассические методы, исследовал ν ≠ 0 переходы. Он рассматривал переход из n-вакуума при t = – ∞ в (n + ν)-вакуум при t = + ∞ как туннельный переход и оценил вероятность туннелирования в методе WKB

A[ν] ~ e−SE [ν] ,

(5.64)

где SE – минимальное евклидово действие калибровочной теории.

Такое минимальное действие реализуется на полевых конфигурациях, называемых инстантонами (Белавин, Поляков, Шварц, Тюпкин). Это самодуальные решения полевых уравнений в евклидовом

пространстве	Gμν = G		μν		,	и их действие связано с ν.			Для этих
решений		a	a
решений							8π2
		SE [ν] =		1	∫	d 4 xEGaμνGaμν =	8π2	ν .	(5.65)
		SE [ν] =		4		d 4 xEGaμνGaμν =	g32	ν .	(5.65)
				4			g32

Как показал Т’ Хоофт, константа связи, входящая в SE [ν] , – это

«бегущая» константа связи, определяемая на характерном инстантонном масштабе. Для оценки амплитуды надо проинтегрировать по всем масштабам

		2πν
A[ν] ~ ∫dρexp	−		.	(5.66)
A[ν] ~ ∫dρexp	−	α ρ−1	.	(5.66)
		3

В КХД из-за роста на больших масштабах квадрата константы связи α3ρ−1 для инстантонов больших размеров нет дополнительного подавления в факторе туннелирования. Вследствие этого невозможно вычислить A[ν], но можно ожидать, что

A[ν ≠ 0] ~ A[0].

(5.67)

Таким образом, U(1)А не является симметрией KXД.

Многое из того, что обсуждалось выше, применимо к электрослабой теории. Однако, как мы увидим ниже, есть и существенное отличие. Поскольку электрослабая теория основана на группе SU(2)×U(1), то наличие SU(2) фактора ведет к нетривиальной ваку-

умной структуре. WW плотность связана с разностью индекса и с дивергенцией (B + L) тока

186

g22

μν

∂

B+L

= −

(5.68)

16π2

g i

iμν

Следовательно, изменение в (B+L) электрослабой теории тоже связано со слабым индексом ν:

	(B + L) = ∫d 4 x∂μJBμ+L =									(5.69)
	g22			∫		4	μν			(5.69)
= −		N	g		d		xW W	= −2N	g	ν.
= −		N			d		xW W	= −2N		ν.
	16π2						i iμν
	16π2

Заметим, что для трех поколений ( N g =3) минимальное нарушение (B+L) пока составляет [ (B+L)] = 6. Поэтому, если даже барионное число нарушено, в стандартной модели процесс p → e+π0 , кото-

рый соответствует [ (B+L)] = 2, остается подавленным! Гораздо важнее, однако, что амплитуда (B+L) нарушения чрезвычайно мала. Эта амплитуда, по крайней мере квазиклассически, задается тем же способом, как в КХД (и заменой α3 → α2 ) . Однако, из-за наруше-

ния электрослабой симметрии, интегрирование по инстантионным размерам обрезается на величине υ (или на масштабе импульсов порядка Mz), т.е.

Заметим, несмотря на то, что этот фактор пренебрежимо мал, в ранней Вселенной (B+L) нарушение в электрослабой теории может быть важным. Кузьмин, Рубаков и Шапошников показали, что в температурной среде калибровочные конфигурации, связанные с (B+L) нарушающими процессами, определяются не фактором туннелирования, а больцмановским фактором. Вблизи фазовых переходов больцмановский фактор стремится к единице, и (B+L) нарушающие процессы становятся неподавленными.

5.4. Сильная СР проблема

θ-вакуум КХД является новым источником СРнарушения. Что касается эквивалентного θ параметра в электрослабой теории, то он

187

может быть исключен вследствие киральной природы этих взаимодействий.

В КХД же лагранжиан эффективного взаимодействия

LCP−наруш. = θ	α3 μν
LCP−наруш. = θ	8π Ga Gaμν ,	(5.71)

отражающий присутствие вакуумного угла. Однако ситуация из-за электрослабых взаимодействий несколько усложняется. Напомним, что кварковые массовые матрицы, возникающие при спонтанном нарушении SU(2)×U(1), не являются ни эрмитовыми, ни диагональными

L = −q

− q

(M + )

Lj .

(5.72)

масс

Эти матрицы диагонализируются при соответствующих унитарных преобразованиях кварковых полей

qR → qR′ =U RqR ; qL → q′L =U LqL .

(5.73)

Легко проверить, что часть этих преобразований включает U(1)А преобразование. Действительно, U(1)Ачасть этих преобразований

		i
qR → q′R = exp
qR → q′R = exp		2n f
		2n f

		i
qL → q′L = exp	−	i
qL → q′L = exp	−	2n f
		2n f

	i
Arg det M qR ≡ exp			α qR ;
Arg det M qR ≡ exp			α qR ;
	2
				(5.74)
			i	(5.74)
			i
Arg det M qL ≡ exp		−		α qL .
Arg det M qL ≡ exp		−	2	α qL .
			2

Оказывается, что такие U(1)А преобразования вызывают изменение вакуумного угла, т.е. вносят вклад в выражение (5.71), помимо КХД угла θ.

Чтобы прояснить это заключение, следует более внимательно исследовать результат кирального U(1)А преобразования. Хотя ток

J5μ , связан с U(1)А аномалией, всегда оказывается возможным по-

строить сохраняющийся ток, используя ток K μ , входящий в тождество Бардина. Обращаясь к соотношениям (5.53) и (5.62), находим желаемый сохраняющийся киральный ток

μ	μ		n f α3		μ
J5	= J5	−	4π	K		.	(5.75)
			4π
		188

Заряд, генерируемый киральными преобразованиями Q5 , должен

быть независящим от времени, и он связан с J5μ сохраняющимся током

Q5 = ∫d 3xJ50 .

(5.76)

Хотя Q5 не зависит от времени, этот заряд неинвариантен относи-

тельно калибровочных преобразований, поскольку K μ не является калибровочно-инвариантным током. Найдем

Ω1Q5Ω1			n f α3	∫d 3 xK 0
	= Ω1 Q5	−			Ω1	= Q5	+ n f .	(5.77)
			4π

Рассмотрим действие большого калибровочного преобразования Ω1 на кирально-вращательный θ-вакуум eiαQ5 θ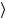 . Получаем

Ω	eiαQ5	θ	= Ω eiαQ5	Ω−1Ω	θ = ei(αn f +θ) eiαQ5	θ	. (5.78)

1			1	1 1

Отсюда видно, что киральное U(1)А вращение действительно сдвигает вакуумный угол

eiαQ5	θ =	θ+ αn f .	(5.79)

Для электрослабой теории киральное вращение, необходимое для диагонализации кварковых массовых матриц, имеет параметр

α =	1	det M . Таким образом, эффективный СР-нарушающий ла-

	n f

гранжиан, возникающий из структуры калибровочной теории вакуума, имеет вид

эф

α3

μν

= θ

(5.80)

8π

aμν

СР−нар

где

= θ+ Argdet M .

(5.81)

Эффективный СР-нарушающий параметр θ есть сумма КХД вклада (вакуумный угол θ) и электрослабой части (Arg det M), связанной со структурой кварковой массовой матрицы.

Взаимодействия (5.80) С – четны, Т и Р – нечетны. Таким образом, они нарушают СР-инвариантность.

189

Как будет видно ниже, несмотря на то, что θ очень мал (θ <10−10 ) , это взаимодействие индуцирует электрический ди-

польный момент нейтрона. Трудно понять, почему параметр θ , который представляет собой сумму двух очень различных вкладов, оказывается столь малым. В этом состоит суть так называемой сильной СР-проблемы.

Прежде чем обсуждать дальше сильную СР проблему, рассмотрим, как с помощью эффективного лагранжиана (5.80) найти электрический дипольный момент нейтрона. Это легко сделать, трансформируя θ-взаимодействие, включающее глюоны, во взаимодействие, содержащее кварки.

Для простоты остановимся на случае двух ароматов (n f = 2) и положим mu = md = mq . Тогда киральное U(1)А преобразование

u			5 u
		θγ		(5.82)
	→ exp i	4
d			d

вносит вклад в θGG член. Однако преобразование (5.82) будет в то же время генерировать СР-нарушающий γ5-зависящий массовый член для u и d-кварков

эф

γ5

LСР−нар = iθmq u

u + d

d .

(5.83)

Этот лагранжиан можно непосредственно использовать для вычисления электрического дипольного момента нейтрона

dnnσμνK νγ5n =	n T (Jμэлектрi∫d 4 xLэфСР−нар	n ).	(5.84)

Чтобы найти dn , нужно вставить полный набор состояний x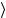 в матричный элемент (5.84) и попытаться определить, какой набор состояний x 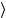доминирует. В литературе существуют два подхода к этой проблеме. В одном из них для x 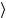используются нечетные

N1/2− состояния, связанные с нейтроном посредством лагранжиа-

на LэфСР−нар .

190

<<< < Предыдущая 7 8 9 10 11 12 13 14 15 16 17 1819 / 5619 20 21 22 23 24 25 26 27 28 29 30 31 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
16.08.2013616.13 Кб36Елманов Моделирование процессов вакуумной плавки металлов 2008.pdf
#
16.08.20131.25 Mб49Елманов Теплоемкост металлов и сплавов 2007.pdf
#
16.08.20131.15 Mб69Елманов Теплопроводност металлов и сплавов 2007.pdf
#
16.08.20132.72 Mб95Елтаренко Исследование операцыи 2007.pdf
#
16.08.20133.97 Mб132Емелянов Лекции по основам електрослабой 2007.pdf
#
16.08.201311.16 Mб109Емелянов Фундаменталные симметрии 2008.pdf
#
16.08.2013507.34 Кб13Енглиш-Руссиан дицтионары оф енглиш фор манагерес 2009.pdf
#
16.08.20138.42 Mб235Ермолаев Технологические процессы в машиностроении 2011.pdf
#
16.08.20131.2 Mб71Жабрев Лабораторный практикум Получение и 2007.pdf
#
16.08.20139.04 Mб223Жданов Основы физических процессов 2007.pdf
#
16.08.20136.4 Mб244Жданов Тайны разделения изотопов 2011.pdf