
Емелянов Фундаменталные симметрии 2008
.pdfчастицы, т.е. dνe ≠ dνe . Подобные неравенства справедливы для всех лептонов и кварков, следовательно, и для адронов.
6.6.5. СРТ и эрмитовость
Что могло бы означать обнаружение циркулярной поляризации фотонов от распада π0 → γγ (или η → γγ )? Легко понять, что это
наблюдение означало бы нарушение СРТ-симметрии. Действительно, С сохраняется в этом распаде, в то время как произведение
S k Р-нечетно, но Т-четно ( S и k – фотонный спин и импульс). Подобное же рассуждение применимо к продольным поляризациям
мюонов в распаде π0 → μ+μ− , наблюдаемым на уровне 6 10-6. Корреляция Sμ kμ Р-нечетная и Т-четная. С другой стороны, она должна быть С-четной, поскольку η0 – С-четное. Поэтому наблюдение Sμ kμ корреляции свидетельствовало бы о СРТ-нарушении.
Обсудим два слагаемых в лагранжиане, интерференция которых
могла бы привести к корреляции S k в распаде π0 → γγ . Первое из них – скаляр gϕFμνFρδεμνρδ , второе – псевдоскаляр hϕFμνF μν , где
φ-псевдоскалярное пионное поле, которое С-четное, Р-нечетное и Т-нечетное.
Вследствие эрмитовости лагранжиана, величины g и h должны быть вещественными. Степень же циркулярной поляризации фотонов пропорциональна g*h − gh* . Следовательно, для эрмитового
лагранжиана циркулярная поляризация на древесном уровне должна обращаться в ноль. Она могла бы появиться из-за разности поглощательных частей рис. 6.3 в скалярных и псевдоскалярных амплитудах.
Если же степень поляризации оказывается другой по сравнению с диаграммой на рис. 6.3 , то это означает нарушение эрмитовости.
Рассмотрим сначала случай, когда Im g = 0, Re h = 0. Тогда член, пропорциональный g, относится к точке 0, член же, пропорциональный h – к точке 2, поскольку он С-четен, Р-нечетен, Т-четен, следовательно, СРТ-нечетен.
231
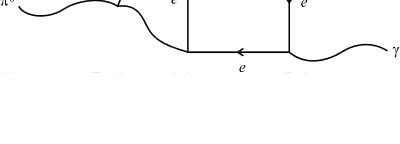
Рис. 6.3
В случае же Re g = 0, Im h = 0 g-член С-четен, Р-нечетен, Т- нечетен, т.е. СРТ-четен (точка 5). Интерференция точек 3 и 5 (а
также точек 2 и 0) дают Р и СРТ нарушающую корреляцию |
S k . |
В общем случае, когда g и h – комплексные |
|
g*h − h*g = 2i Re g Im h − 2i Im g Re h |
(6.107) |
и первый член справа в выражении (6.107) характеризует интерференцию точек 2 и 0, а второй интерференцию точек 3 и 5.
В отличие от случая разности масс частицы и античастицы, примеры СРТ-нарушающих поляризаций могут быть сформулированы лоренц-инвариантным образом. На языке лагранжиана, СРT- нарушающие члены имеют «неправильную» фазу, нарушающую эрмитовость. Антиэрмитовы члены в лагранжиане нарушают унитарность S-матрицы.
232

Глава 7 СУПЕРСИММЕТРИЯ И СУПЕРГРАВИТАЦИЯ
7.1. Проблема иерархий
Электрослабый сектор стандартной модели содержит параметр размерности энергии (электрослабый масштаб) – вакуумное среднее хиггсовского поля
υ ~ ГэВ. |
(7.1) |
Этот параметр, в принципе, задаёт масштаб масс в теории. Так, массы W (пренебрегая радиационными поправками):
MW |
= |
gυ |
~ 80 ГэВ, |
(7.2) |
||
|
||||||
|
2 |
|
|
|
|
|
А масса хиггсовского бозона |
|
|
|
|
||
|
M H = υ |
λ |
, |
(7.3) |
||
|
2 |
|||||
|
|
|
|
|
|
|
где g – SU(2) калибровочная константа, λ – константа самовзаимодействия в хиггсовском потенциале
V = −μ2φ+φ + |
λ |
(φ+φ)2 |
(7.4) |
4 |
причём λ > 0 и μ2 > 0.
В потенциале (7.4) поле φ – SU(2) дублет:
|
φ+ |
|
||
φ = |
φ |
0 |
. |
(7.5) |
|
|
|
|
|
Заметим, что отрицательный знак перед μ2 существенен, поскольку только в этом случае “работает” механизм спонтанного нарушения симметрии. При этом минимум потенциала
|
φ |
|
= |
2μ |
≡ |
υ |
(7.6) |
|
|
||||||
|
|
λ |
2 |
||||
|
|
|
|
|
|
интерпретируется как ненулевой минимум классического потенциала. В свою очередь, классический минимум следует рассматривать как вакуумное среднее квантового поля. Если (–μ2) в потенциале заменить положительной величиной μ2, то классическое рав-
233

новесное значение будет в начале координат V = 0, и все частицы будут безмассовыми. Однако всё это справедливо на древесном уровне (без учёта петлевых поправок). Что произойдёт, если учесть петлевые поправки? Стандартная модель – перенормируемая теория, а это значит, что она даёт конечный результат с учётом всех поправок (петель) высших порядков, даже если виртуальные импульсы во всех петлях устремить к бесконечности. Однако это не означает, что в петлевых интегралах
Λ |
|
∫ d 4 Kf (K, внешние импульсы) |
(7.7) |
следует считать параметр обрезания Λ стремящимся к бесконечности. Более обосновано, пожалуй, считать стандартную модель частью более общей теории, которая включает неизвестную пока “новую физику” при больших энергиях. Параметр Λ – это масштаб, на котором появляется новая физика и на котором необходимо модифицировать стандартную модель. В конце концов, мы ожидаем новую физику на масштабах, когда становятся существенными эффекты квантовой гравитации. Этот масштаб называют планковской массой
M Pl = (GN )−1/2 ~ 1, 2 1010 ГэВ. |
(7.8) |
Если M Pl – действительно масштаб новой
физики, то при учёте петлевых поправок в стандартной модели возникают серьёзные трудности. Действительно, четырёхбозонное взаимодействие в соотношении (7.4) в одно-
Рис. 7.1 петлевом приближении даёт вклад в собственную энергию, представленный на рис. 7.1.
Этот вклад пропорционален
Λ |
|
1 |
|
|
|
λ∫ d 4 K |
|
|
. |
(7.9) |
|
K |
2 |
2 |
|||
|
|
− M H |
|
||
Интеграл квадратично расходится и даёт поправку |
|
||||
λΛ2φ+φ |
(7.10) |
||||
к слагаемому –μ2φ+φ в потенциале V. |
|
||||
234

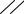
Почему же получается δm ~ m ? Дело в том, что лагранжиан КЭД в пределе m→0 кирально инвариантен. При киральных преобразованиях
Ψ → eiαγ5 Ψ |
(7.15) |
||||
для U(1)-симметрии и |
|
|
|
||
|
iατ |
γ5 |
|
|
|
Ψ → e 2 |
Ψ |
(7.16) |
|||
|
|||||
в SU(2)-случае.
Киральная симметрия гарантирует, что все радиационные поправки к массе m, вычисленные в теории возмущений, будут исчезать в пределе m→0. Поэтому поправки к δm должны быть пропорциональны m, а зависимость от Λ (даже из соображений размерности) – только логарифмическая.
Что происходит с поправками к массам калибровочных частиц? В КЭД ненарушенная калибровочная симметрия обеспечивает mγ → 0 во всех порядках теории возмущений. Другими словами,
калибровочная инвариантность гарантирует, что члены вида
m2 Aμ A |
(7.17) |
|
γ |
μ |
|
могут генерироваться за счёт радиационных поправок в ненарушенной калибровочной теории. С другой стороны, ненулевые массы W и Z-бозонов в стандартной модели возникают на непертурбативном уровне посредством спонтанного нарушения симметрии и вакуумного среднего υ. Если υ≡0, то W, Z, как и фотон, будут безмассовыми. Но υ μ, поэтому массы, приобретаемые W и Z при
нарушении симметрии, чувствительны к Λ и MH. Можно ли найти симметрию, которая бы, подобно киральной или калибровочной симметрии, контролировала бы поправки δm к массе скалярных частиц в лагранжиане? Очевидно, что существуют фермионные петлевые поправки к -μ2φ+φ, в которых частица φ переходит в фер- мион-антифермионную пару, которая затем снова аннигилирует в φ-частицу. Этот процесс даёт вклад
−g 2f |
∫ |
d 4 K |
φ+φ g 2f |
φ+φΛ2 . |
(7.18) |
KK |
|||||
|
|
||||
|
|
|
236 |
|
|
Знак этого выражения существенен, он возникает за счёт замкнутой фермионной петли. Объединяя (7.10) и (7.18), получаем полную однопетлевую поправку
(λ − g 2f )Λ2 |
φ+φ . |
(7.19) |
Сразу возникает соблазн приравнять |
|
|
λ = g 2f |
, |
(7.20) |
тогда квадратичная по Λ поправка обратится в ноль. Именно такое сокращение происходит в суперсимметричных теориях. После сокращения члена с Λ2 две диаграммы для собственной энергии хиггсовского бозона дают
~ λ(M H2 − m2f )ln Λ . |
(7.21) |
Эта поправка может быть порядка M H2 , если все бозоны и фер-
мионы в теории имеют массы, не превышающие нескольких ТэВ. Частицы, участвующие в механизме сокращения расходимостей, должны быть приближенно вырожденными (указывая на приближённый характер SUSY) и не слишком превышать по массе υ (или
M H ).
Таким образом, SUSY стабилизирует иерархию M H ,W << M Pl в
том смысле, что радиационные поправки не смещают MH,W к большому Λ.
7.2. Теоретические основы SUSY
Как мы уже многократно подчёркивали, идея симметрий оказалась весьма плодотворной как в физике вообще, так и в физике элементарных частиц, в частности. Правомерно задать вопрос: используются ли в современных квантовых теориях поля все симметрии, совместимые с лоренц-инвариантностью?
Обратимся к симметриям зарядов, известных в стандартной модели. Начнём с электрического заряда
Q = e∫d 3 xΨ+Ψ |
(7.22) |
или SU(2)-заряда (изоспинового заряда)
237
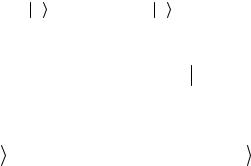
T = g∫d |
3 |
xΨ |
+ |
τ |
Ψ , |
(7.23) |
|
|
|
|
|
||||
|
|
||||||
|
|
|
|
2 |
|
|
|
где в выражении (7.23) Ψ – SU(2) дублет. Как в (7.22), так и в (7.23) Ψ – фермионное поле.
Все эти операторы симметрии являются лоренцевскими скалярами (они не несут лоренцевских индексов, как вектора или спиноры). Если эти спиноры действуют на состояние с определённым
спином, то они не могут изменить спин: |
|
Q|Ι >=| тот же I, но другой член мультиплета>. |
(7.24) |
Нам известен один “векторный” заряд – оператор 4-импульса, генерирующий пространство-временные смещения, чьи собственные значения – сохраняющиеся 4-импульсы. Операторы углового мо-
мента относятся к антисимметричным тензорам Mμν. Есть ли дру-
гие сохраняющиеся симметричные тензорные заряды Qμν?
Таких зарядов нет. В самом деле, выберем заряд, действующий
на состояние частицы с 4-импульсом p: |
|
Qμν p = (αpμ pν +βgμν) p , |
(7.25) |
где правая часть записана из соображений ковариантности (наиболее общее выражение из имеющихся в нашем распоряжении тензо-
ров). Далее выберем двухчастичное состояние p(1) , p(2)  и пред-
и пред-
положим, что Qμν аддитивны, сохраняются и действуют в каждый момент времени лишь на одну частицу, как обычные заряды.
Тогда
Q |
p(1) , p(2) = (α( p(1) p(1) |
+ p(2) p(2) ) + 2βg |
μν |
) |
p(1) |
, p(2) |
. (7.26) |
μν |
μ ν |
μ ν |
|
|
|
|
При упругом рассеянии 1+2→3+4 необходимо считать (из-за сохранения собственных значений)
p(1) p(2) |
+ p |
(2) p(2) |
= p(3) p(3) |
+ p(4) p(4) . |
(7.27) |
|
μ ν |
|
μ ν |
μ |
ν |
μ ν |
|
В силу сохранения 4-импульса |
|
|
|
|
||
|
p(1) |
+ p(2) |
= p(3) |
+ p(4) . |
(7.28) |
|
|
μ |
μ |
μ |
|
ν |
|
Общее решение уравнений (7.27) и (7.28):
238

pμ(1) = pμ(3) , pμ(2) = pμ(4) или pμ(1) = pμ(4) , pμ(2) = pμ(3) . (7.29)
Последние условия означают, что рассеяние происходит только вперёд или только назад. Очевидно, что такое ограничение слишком обременительно. Можно сделать вывод: не существует других
сохраняющихся операторов (кроме Pμ и Mμν) с нетривиальными лоренцевскими трансформационными свойствами (т.е. не лорен-
цевских скаляров). Существование операторов Pμ и Mμν допускает всевозможные процессы рассеяния. Допущение других законов сохранения жёстко ограничивает возможные конфигурации.
Эти рассуждения, однако, не исключают заряды, преобразующиеся при Лоренц-преобразованиях как спиноры, т.е. как фермионные поля. Можно обозначить такой заряд через Qa , где индекс “a” указывает на спинорную компоненту. Для такого заряда соотношение (7.24) уже не выполняется:
Qa |
|
I = |
|
I ±1/ 2 . |
(7.30) |
|
|
Такой оператор не даёт вклада в матричный элемент прогресса упругого рассеяния 2→2, поскольку спины частиц не меняются.
Возникает вопрос: можно ли включить такие спинорные опера-
торы, наряду с Pμ и Mμν в согласованную алгебраическую схему? Положительный ответ на этот вопрос был дан в рамках алгебры суперсимметрии Гельфандом и Лихтманом. Под алгеброй, как обычно, понимается набор коммутационных соотношений между “зарядами”, являющимися генераторами соответствующих преобразований симметрии. Однако заряды, имеющие спинорный характер, должны антикоммутрировать между собой. Поэтому алгебра суперсимметрии содержит как коммутационные, так и антикоммутационные соотношения. Как выглядит эта алгебра? Поскольку спинорные заряды Qa – операторы симметрии, они должны коммутировать с гамильтонианом системы:
[Qa , H ] = 0 , |
(7.31) |
антикоммутатор двух зарядов тоже коммутирует с гамильтонианом:
{Qa ,Qb} , H |
= 0 . |
(7.32) |
|
|
|
|
|
|
239 |
|
|
Отметим, что спинорные Qa имеют две компоненты, т.е. симметричный объект {Qa , Qb} = QaQb + QbQa имеет три независимые
компоненты, и поэтому должны преобразовываться как объекты со спином 1 (точно так же, как симметричная комбинация двух волновых функций со спином 1/2). Но в релятивистской теории объект со спином 1 должен описываться 4-вектором, а не 3-вектором. Этот 4-вектор, согласно соотношению (7.32), сохраняется. Существует
лишь один такой сохраняющийся оператор Pμ. Поэтому Qa должен удовлетворять алгебре, в которой
{Qa ,Qb} ~ Pμ . |
(7.33) |
Однако в выражении (7.33) нет баланса индексов справа и слева. Этот вопрос будет рассмотрен ниже, здесь же мы обсудим, в чём заключается основная идея суперсимметрии. Из соотношения (7.33) следует, что если провести два SUSY преобразования, генерируемых операторами Qa, получим оператор энергии-импульса. Или, другими словами, получим оператор пространственновременной трансляции или производную. Можно сказать, что спинорные операторы SUSY Qa ведут себя как квадратные корни из 4- х импульсов или как квадратные корни из производных. Четырёхмерные производные жёстко связывают наши представления с четырёхмерным пространством-временем. Обсуждая сейчас возможности существования квадратных корней из этих производных, мы существенно расширяем концепцию пространства-времени. Наверное, здесь правомерна аналогия с введением квадратного корня из (–1) и расширением вещественной оси в комплексную плоскость. Таким образом, следует допустить, что пространственновременные координаты значительно расширяются за счёт включения других степеней свободы, причём новые степени свободы связаны со стандартными степенями свободы преобразованиями, генерируемыми операторами Qa. Эти новые степени свободы – фермионные. SUSY расширяет пространство-время до суперпространства, вводя “фермионные измерения”.
Часто говорят, что SUSY подразумевает (если это точная симметрия) вырожденность мультиплетов бозонов и фермионов.
240
