
Жданов Основы физических процессов 2007
.pdf
rj = −|e|ne vre .
Используя принятые обозначения, запишем:
• Закон сохранения массы (неразрывности струи):
∂ρ |
+ div( ρvr) = 0 . |
(3.4) |
∂t |
•Уравнение движения единицы объема плазмы (сохранения им-
пульса):
|
dvr |
|
1 r |
r |
r |
|
|
ρ |
|
= |
|
j |
× B − p + F , |
(3.5) |
|
dt |
c |
||||||
где p=pe+pi - полноеrдавление плазмы, равное сумме давлений электронов и ионов, F - внешняя сила (например, сила тяжести),
dvr |
|
∂vr |
r r |
|
|
= |
∂t |
+ ( v )v |
− полная производная (так называемая субста- |
dt |
циональная производная) по времени от скорости плазмы. Уравнение (3.5) может быть получено суммированием уравне-
ний движения для электронов и ионов (см. формулу (2.1)) с последующим пренебрежением конечностью инерции электронов. Во многих конкретных случаях в уравнении (3.5) силой F можно пренебречь.
• Уравнения Максвелла:
div E = 4πρq = 4π|e|( zni − ne );
div B = 0 ; |
|
(3.6) |
|||
r |
|
1 ∂ B |
|
||
rot E = − |
|
|
∂t |
; |
|
c |
|||||
r |
4π r |
|
|||
rot B = |
|
|
j . |
|
|
c |
|
||||
Предполагается, что все процессы медленные и токами смещения можно пренебречь, что и использовано в последнем из уравнений
(3.6).
• Закон Ома (согласно [13]): |
|
|
|
|
|
|
|
|||||
r |
rj |
|
j || |
1 |
|
r |
r |
|
||||
E′ = |
|
|
+ |
|
|
+ |
|
|
|
j |
× B , |
(3.7) |
σ |
|
σ |
cn |
|e| |
||||||||
|
|
|
|| |
|
|
e |
|
|
|
|
|
|
131

где Е′ - эффективное поле, обусловленное в общем случае не только приложенной внешней ЭДС, но и самим движением плазмы, а также наличием электронного давления и перепада электронной температуры; σ||, - продольная и поперечная (по отношению к на-
1 r r
правлению магнитного поля) проводимость плазмы; cne|e| j × B -
холловское поле.
Употребительно несколько различных форм записи закона Ома для плазмы. Это связано с тем, что в зависимости от конкретных условий может оказаться наиболее существенной та или иная причина возникновения ЭДС (подробнее см.[13]). Часто используется следующая упрощенная форма записи закона Ома:
r |
r |
1 r |
r |
1 r |
r |
1 |
|
|
|
|||
j |
= σ E + |
|
v |
× B − |
|
j |
× B + |
|
|
p . |
(3.8) |
|
c |
n|e|c |
n|e| |
||||||||||
|
|
|
|
|
|
e |
|
|||||
• Уравнение состояния − это соотношение вида: |
|
|||||||||||
|
|
|
|
p = p( ρ,T ) . |
|
|
|
(3.9) |
||||
Уравнение состояния приобретает простой вид, если плазму можно считать идеальной. Для классического идеального газа, как известно, уравнение состояния
р = nT.
где n – концентрация (плотность числа частиц) газа. Для смеси двух идеальных «газов» − «газа» электронов с концентрацией ne и «газа» ионов с концентрацией ni
p= neTe+niTi.
Вчастном случае идеальной квазинейтральной изотермической
плазмы, когда температуры и концентрации ее компонент совпадают Te=Ti=Т, ne=ni=n, это уравнение приобретает особенно простой вид
p = 2nT. |
(3.10) |
Но теперь в уравнениях динамики плазмы появляется дополнительный параметр − температура, и необходимо указать правило его вычисления, выражающее баланс тепла. В общем случае это достаточно сложное уравнение, учитывающее конечную теплопроводность плазмы, вязкое тепловыделение, джоулево тепло, обусловленное протеканием по плазме тока и другие источники нагре-
132
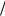
ва или охлаждения плазмы. Мы не будем его выписывать, детальный анализ баланса тепла в плазме можно найти, например, в [13]. Применительно к рассматриваемой одножидкостной магнитной гидродинамике в конкретных приложениях часто используются различные упрощенные подходы. Например, для медленных, существенно дозвуковых, течений, плазму приближенно можно считать несжимаемой, ρ=const , и тогда, согласно уравнению неразрывности (3.4), течение плазмы удовлетворяет условию divv = 0 , а дав-
ление плазмы определяется условием совместимости динамических уравнений. В условиях, когда теплообмен с окружающей средой несуществен, используется адиабатический закона вида
p ~ ργ . При этом изменение температуры следует соотношению
T ~ ργ −1 . Здесь γ |
− показатель адиабаты, например, |
для модели |
одноатомного газа |
равный γ=5/3. В общем случае, |
напомним, |
γ = 1 + 2 N , где N=1,2,3… - число степеней свободы. |
|
|
Используя приведенные уравнения магнитной гидродинамики, можно описать поведение плазмы во многих весьма сложных случаях. Несомненным преимуществом такого подхода к описанию плазмы является его сравнительная простота и наглядность. Иногда это очень важно, например, при описании динамики токовых систем. При этом, конечно, в каждом конкретном случае, используя уравнения магнитной гидродинамики плазмы, необходимо иметь в виду условия (3.3) применимости гидродинамических представлений.
§ 23. Магнитное давление
Весьма важные выводы общего характера могут быть получены непосредственно из анализа уравнений (3.4) и (3.5).
В пренебрежении внешними силами F , движение плазмы определяется силой Ампера (иначе называемой пондеромоторной силой) и градиентом газокинетического давления
|
dvr |
|
1 r |
r |
|
|
ρ |
|
= |
|
j |
× B − p . |
(3.11) |
dt |
c |
|||||
133
Используя известное тождество из векторного анализа, справедли-
вое для двух любых векторов a и b ,
( abr )=( ar )b +( b )ar + ar × rotb + b × rotar ,
и уравнение (3.6), пондеромоторную силу можно представить в виде:
|
1 rj × B = |
1 |
rotB × B |
= − B |
2 |
+ |
|
1 ( B )B ≡ − p$ |
маг . (3.12) |
||||||||||
|
|
r |
|
r r |
|
|
|
|
|
|
|
|
|
|
r r |
|
|
|
|
|
c |
4π |
|
|
|
|
|
|
8π |
|
|
4π |
|
|
|
|
|||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
p$маг = |
|
B |
2 |
|
|
|
|
|
^ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
(δ$ − |
2 ττ ), |
|
(3.13) |
|||||||||
|
|
|
|
|
8π |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
||||
|
|
|
|
|
|
|
|
|
δ$ - |
|
|
|
|
r |
|
B |
|||
тензор магнитного давления; |
единичная матрица, а τ |
= |
|
− |
|||||||||||||||
B |
|||||||||||||||||||
единичный вектор, направленный по касательной к силовой линии магнитного поляr . В системе координат с осью z, направленной
вдоль вектора B , этот тензор записывается в виде следующей диагональной таблицы:
|
|
B |
2 |
0 |
0 |
|
|
||
|
|
|
|
|
|||||
|
8π |
|
|||||||
|
|
|
B2 |
|
|
|
(3.14) |
||
p$ |
|
0 |
|
0 |
. |
||||
маг = |
|
|
|
|
|||||
|
8π |
|
|||||||
|
|
|
|
|
|
|
B2 |
|
|
|
|
0 |
0 |
|
|
|
|
||
|
|
|
|
||||||
|
|
− 8π |
|
||||||
Знак компонент тензора магнитного давления не случаен: поперечные компоненты положительны, что соответствует расталкиванию силовых линий магнитного поля в поперечном направлении, тогда как продольная компонента этого тензора отрицательна − в продольном направлении силовые линии натянуты.
Величину
pm = |
B2 |
(3.15) |
|
8π |
|||
|
|
обычно называют магнитным давлением.
134

Полезно так переписать соотношение (3.12), чтобы расталкивание и натяжение силовых линий проявлялись в нем еще более явно. Для этого, пользуясь определением касательного вектора, запишем
( B )B = ( Bτr )( Bτr) = B2 (τr )τr + Bτr(τr B ).
Учитывая, далее, что по определению
(τr )τr = nr , R
где n - нормаль к силовой линии, а R - радиус ее кривизны, получим
1 r |
r |
B2 |
B2 r |
|
|||
|
j |
× B = − |
|
+ |
|
n , |
(3.16) |
c |
8π |
4πR |
|||||
где обозначено для краткости
= − τ (τ ) .
Первое слагаемое в (3.16) отвечает фарадеевскому “расталкиванию”, а второе, связанное с искривлением магнитной силовой линии, описывает влияние натяжения магнитных силовых линий, или фарадеевское “сокращение длины”. Подчеркнем, что в вакууме, то
есть в области вне токов, когда j ≡ 0 , из (3.16) следует соотношение
B = nr ,
B R
которое уже использовалось нами ранее при обсуждении дрейфового движения частиц плазмы в неоднородном магнитном поле. Обе формы записи (3.12) и (3.16) вполне равнозначны, и можно пользоваться любой из них.
Таким образом, пондеромоторная сила может быть представлена в виде суммы градиента магнитного давления и компоненты, обязанной своему появлению натяжению магнитных силовых линий. В однородном поле имеем R→∞, и вклад от этой компоненты обращается в нуль.
В проблеме магнитного удержания плазмы важную роль играет параметр
β = |
p |
= |
8πp |
, |
(3.17) |
pm |
B2 |
135
определяющий отношение газокинетического давления плазмы к магнитному давлению. В зависимости от величины этого параметра принято говорить о плазме высокого давления, если β>1, или о плазме низкого давления, если β<1. Например, в токамаках принципиально может удерживаться только плазма низкого давления, βmax<0.1. В то время как в открытых ловушках в принципе возможно удержание плазмы с β ~1.
Отметим в заключение, что, так как магнитное давление, определенное формулой (3.15), является одновременно и плотностью магнитной энергии, то pm измеряется в эрг/см3, если магнитная индукция В измеряется в гауссах.
§ 24. Равновесие плазмы в магнитной гидродинамике
Важный круг задач, в которых с успехом применяется магнитная гидродинамика, связан со стационарными течениями плазмы, т.е. с такими, когда параметры течения явно не зависят от времени и частные производные по времени в уравнениях (3.4) − (3.10) можно опустить. Частным случаем стационарных процессов являются статические равновесия, когда скорость плазмы тождественно равна нулю. Это именно равновесия, так как из условия vr = 0 вытекает dvr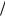 dt = 0 , а, следовательно, действующие на любой эле-
dt = 0 , а, следовательно, действующие на любой эле-
ментарный объем плазмы силы должны быть уравновешены. При этом, как это видно из уравнения движения (3.5), должно быть выполнено условие:
1 r |
r |
|
|
|
j |
× B = p . |
(3.18) |
c |
|||
Это условие и представляет собой уравнение равновесия плазмы в магнитнойr r гидродинамике. Из него, очевидно, следует, что вектора
j и B лежат на поверхностях, ортогональных к градиенту давле-
ния, то есть на поверхностях постоянного давления p=const. С другой стороны, если магнитной конфигурации сопоставить семейство магнитных поверхностей, на которых лежат силовые линии, то, очевидно, что именно на этих поверхностях давление плазмы должно быть постоянно. Таким образом, магнитные поверхности
136

удерживающего плазму магнитного поля с необходимостью должны быть изобарическими для плазмы.
В простейшем случае, когда силовые линии магнитного поля являются прямолинейными и параллельными друг другу, их радиус кривизны равен бесконечности, то согласно выражению (3.16) можно записать
1 r |
r |
B2 |
|
||
|
j |
× B = − |
|
. |
(3.19) |
c |
8π |
||||
Выбрав направление силовых линий за ось z системы координат, для единственной отличной от нуля компоненты поля Bz из уравнения соленоидальности магнитного поля
div B = 0
получим
∂
∂ z Bz = 0 ,
и магнитная индукция может меняться только поперек направления силовых линий. Воспользовавшись представлением (3.19) для силы Ампера, из уравнения (3.18) получим
|
B |
2 |
|
∂ |
|
|
|
z |
|
+ p = 0 , |
|
p = 0 , |
|
8π |
∂ z |
|||||
|
|
|
||||
следовательно, давление плазмы также не меняется вдоль силовых линий, а поперек силовых линий должна быть постоянна сумма давления плазмы и магнитного давления:
Bz 2 + p = const . 8π
Согласно этому условию вне области, занятой плазмой, магнитное поле является однородным, пусть здесь Bz=B0. Тогда постоянную можно выбрать так, что во всем пространстве будет
B |
2 |
|
B |
2 |
|
|
|
z |
|
+ p = |
0 |
|
. |
(3.20) |
|
8π |
8π |
||||||
|
|
|
|||||
Видно, что в области, занятой плазмой, магнитное поле меньше внешнего. Можно сказать, что плазма «выталкивает» магнитное поле, как и любой другой диамагнетик.
137
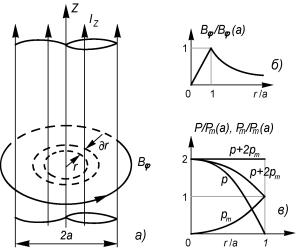
Уравнение (3.20) для рассматриваемого частного случая устанавливает условие равновесного состояния системы “плазма − магнитное поле”, причем давление магнитного поля вне плазмы в равновесии должно быть больше магнитного давления внутреннего поля как раз на величину газокинетического давления плазмы, что наглядно демонстрирует идею удержания плазмы магнитным полем. Подчеркнем, что в уравнениях равновесия нет каких-либо ограничений на происхождение магнитного поля, поэтому оно может быть создано как внешними токами, так и током, протекающим по плазме. Вместе с тем условие (3.20) связывает две неизвестные величины. Поэтому для однозначного решения задачи равновесия необходимо привлекать дополнительные условия, в том числе условия поддержания тока в плазме.
Рис.3.1. Плазменный Z-пинч: а − геометрия токового канала, б − распре-
деление магнитного поля, в −давления плазмы (р) и магнитного давления (pm) по радиусу
Примером квазистационарного процесса может служить равновесное состояние самосжимающегося длинного цилиндрического
138
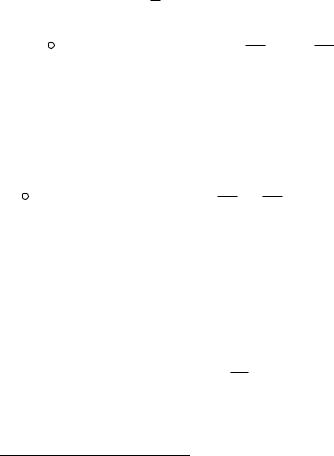
столба плазмы с продольным током - так называемый Z-пинч . В этом случае В и р зависят только от одной координаты - расстояния r от оси столба (рис.3.1). Уравнение равновесия примет вид:
− |
∂p |
= |
1 |
j B . |
|
∂r |
c |
||||
|
|
z ϕ |
Если считать ток пинча распределенным равномерно по его сече-
2
нию, то jz=const и Bϕ = c πrjz , так как по теореме о циркуляции
|
2π |
4π |
|
4π |
|
∫ Bϕ dlϕ |
≡ ∫ Bϕ rdϕ ≡Bϕ 2πr = |
J( r ) ≡ |
πr2 jz , |
||
|
0 |
c |
|
c |
|
|
|
|
|
|
где
r
J( r ) = 2π∫ jz rdr = πr 2 jz
0
− ток в цилиндре с радиусом r. Для области вне пинча, вновь воспользовавшись теоремой о циркуляции, получаем:
2π |
4π |
|
4π |
|
∫Bϕ dlϕ ≡ ∫Bϕrdϕ ≡Bϕ 2πr = |
I ≡ |
πa2 jz , |
||
0 |
c |
|
c |
|
|
|
|
|
где I − полный ток пинча. Таким образом, распределение магнитного поля пинча следующее (рис. 3.1,б):
r |
, r ≤ a |
|
|
|
|
|
||
Bϕ ( r ) = Bϕ ( a ) a |
, |
|
|
a |
, r > a |
|
||
r |
|
|
где
2I Bϕ ( a ) = ca
магнитное поле на границе плазмы.
Отметим попутно полезную практическую формулу для расчета величины этого поля:
Разряд с геометрией Z-пинча возникает, например, при пропускании сильного тока через газ между двумя параллельными электродами, расположенными перпендикулярно оси z.
139

= 0.2I ( А) Bϕ (Гс) a(м) , .
Подстановка распределения поля в уравнение равновесия приводит к соотношению
∂∂pr = − 2cπ2 jz 2 r .
Интегрируем и, учитывая, что на границе столба (при r=a) газокинетическое давление равно нулю (р=0), получаем
|
πa2 |
|
|
r2 |
|
I 2 |
|
r2 |
|
Bϕ2 ( a ) |
|
r2 |
|||||
p = |
c2 |
j2 1 |
− |
|
|
= |
|
1 |
− |
|
|
≡ |
|
1 |
− |
|
. |
|
|
|
4π |
|
|||||||||||||
|
|
|
a2 |
|
πa2 c2 |
|
a2 |
|
|
|
a2 |
||||||
Подчеркнем, что сумма давлений магнитного поля и давления плазмы
p + |
Bϕ2 |
( r ) |
|
Bϕ2 ( a ) |
|
r 2 |
≠ const |
|||
|
|
|
= |
|
2 |
− |
|
|
||
8π |
8π |
|
||||||||
|
|
|
|
a2 |
|
|||||
теперь не является величиной постоянной (сравним с (3.20)). Очевидно, это связано с вкладом от натяжения силовых линий, которые здесь имеют форму окружностей с конечным радиусом кривизны. Постоянной теперь является величина
p + |
Bϕ2 ( r ) |
− ( − |
Bϕ2 ( r ) |
) ≡ p + |
Bϕ2 ( r ) |
= |
Bϕ2 ( a ) |
= const . |
|||
8π |
|
8π |
|
4π |
|
4π |
|||||
Вклад натяжения силовых линий приводит к тому, что давление плазмы в центре токового канала оказывается ровно вдвое больше магнитного давления на его границе. Распределение давлений в токовом канале показано на (рис. 3.1,в).
Так как p=2nT, то, вводя полное число частиц на единицу длины плазменного столба N (так называемое погонное число частиц) и считая температуру плазмы Т постоянной, определим
a |
I |
2 |
|
|
N = 2π∫nr dr = |
|
|
, |
|
4c |
2 |
T |
||
0 |
|
|
||
|
|
|
|
откуда получаем соотношение
I 2 4NT = c2 ,
140
