Жданов Основы физических процессов 2007

сила взаимодействия между заряженными частицами (сила Кулона) значительно медленнее убывает с ростом расстояния между частицами. Именно дальнодействующий характер сил между заряженными частицами и приводит к качественно новым - плазменным - эффектам в газе, содержащем свободные заряды. Это качественно новый газ: газ, содержащий в заметном числе заряженные частицы. Такой газ и называют плазмой. Сам термин “плазма” появился в обиходе науки после работ Ленгмюра и Тонкса в 1928 г., и был введен для описания совокупности явлений, сопровождающих электрический разряд в газе. Легко понять, что между газом нейтральных частиц и газом-плазмой нет четкой границы: обычный газ становится плазмой, как только роль взаимодействия заряженных частиц становится, если не определяющей, то существенной для поведения данной субстанции. Очевидно, что эта граница довольно размытая, в отличие от резких фазовых переходов, имеющих место с повышением температуры и сопровождающих превращение твердого тела в жидкость, а затем жидкости в газ. Некоторое равновесное количество заряженных частиц (определяемое формулой Саха) присутствует в газе при любой температуре, например, свободные заряды в пламени обычной свечи. Но вряд ли столь слабоионизованный газ можно назвать плазмой. Вместе с тем, в дальнейшем мы увидим, что типично плазменные процессы наблюдаются в газе-плазме даже тогда, когда ионизованы только доли процента всех частиц. Можно рассуждать и от обратного: “истинная” плазма состоит из свободных ионов и электронов и остается плазмой до тех пор, пока примесь нейтральных частиц не изменит существенно ее свойств. Но возникает вопрос можно ли, например, назвать плазмой нескомпенсированные по заряду пучки ускоренных частиц, широко используемые в физических экспериментах? Можно ли назвать плазмой весьма разреженный межзвездный или межгалактический газ, ионизуемый излучением звезд? Очевидна необходимость количественного критерия, позволяющего определить, является ли данная совокупность заряженных и нейтральных частиц плазмой. Такой критерий можно сформулировать, опираясь на понятия ленгмюровской частоты и дебаевского радиуса (или длины) экранирования. Именно эти фундаментальные в физике плазмы параметры задают минимальные характерные временной и пространственный масштабы поддержания (или спон-

11

танного нарушения) квазинейтральности плазмы. Опираясь на эти понятия, можно установить, почему плазменные свойства проявляют, на первый взгляд различные среды - электронный газ в металлах, электронно-дырочная “жидкость” полупроводников или, например, разреженный газ космоса.

Эти, а также другие среды, например электролиты, к которым относятся и «рабочие жидкости» живых систем, иногда называют плазмоподобными [3,4]. Это подчеркивает важность характерных для плазмы законов при описании свойств столь большого и важного в практическом применении числа объектов природы. Электронная плазма металлов называется вырожденной. Критерием вырождения, как известно, является соотношение между энергией Ферми, возрастающей с ростом концентрации частиц, и тепловой энергией. Если тепловая энергия меньше энергии Ферми, то плазма вырождена и существенны квантовые эффекты. Мы будем иметь дело с невырожденной плазмой, т.е. с такой плазмой, в которой концентрация заряженных частиц достаточно мала (или температура достаточно велика). Строго говоря, многие физики вводят дополнительные условия - считают, например, обязательной компонентой плазмы электромагнитное излучение. Последнее бесспорно верно для больших объектов из плотной плазмы, например, звезд. В них излучение "заперто" − излучение может выходить лишь из сравнительно тонких наружных слоев. В большинстве лабораторных устройств плазма оптически тонкая, излучение не заперто - оно свободно проходит через всю плазму.

Подведем итоги. По современным представлениям плазма - частично или полностью ионизованный газ, в котором объемные плотности положительных и отрицательных зарядов практически одинаковы. Такое свойство плазмы называют квазинейтральностью. Заряженные частицы плазмы взаимодействуют с силой, для которой характерно дальнодействие. Это обстоятельство определяет исключительную роль в плазме, помимо парных столкновений отдельных частиц, коллективных эффектов, т.е. полей от многих частиц, проявляющихся в нарастании плазменных колебаний, волн и шумов, в свою очередь воздействующих на движение частиц плазмы. Если возбуждается достаточно много коллективных степеней свободы, то колебания плазмы становятся нерегулярными, она переходит в так называемое турбулентное состояние. В этих усло-

12

виях становятся существенными нелинейные эффекты взаимодействия коллективных возбуждений (мод) плазмы. Нелинейные явления могут быть существенны и в регулярных процессах, например, при воздействии на плазму волн конечной амплитуды. Понятно поэтому, что современная физика плазмы − это физика нелинейных явлений. Еще одна особенность этого нового состояния вещества − плазмы − заключается в сильном воздействии на него внешних электрических и магнитных полей, вызывающих появление объемных зарядов и токов. Вместе с тем, существенное разделение зарядов в плазме затруднено в силу ее квазинейтральности: из-за достаточно большой плотности заряженной компоненты в плазме объемный заряд вызывал бы появление слишком больших собственных полей плазмы, чего в действительности не происходит. В определенном смысле квазинейтральность плазмы есть проявление того свойства, что главную роль в плазме играет взаимодействие частиц через самосогласованные поля. В этом отношении динамические процессы в плазме являются весьма сложными явлениями. Они требуют изучения не только динамики частиц в заданных внешних полях, но и одновременного учета влияния собственных, согласованных с движением частиц электромагнитных полей, самым существенным образом сказывающихся на движении самих частиц плазмы.

Взаключение нелишне подчеркнуть, что плазма во Вселенной и

вразнообразных природных процессах и явлениях представлена весьма широко. Межгалактическая, межзвездная и межпланетная плазма, плазма звезд и звездных атмосфер, от Белых Карликов до Красных Гигантов, нейтронных звезд, пульсаров и черных дыр, плазма верхних слоев атмосферы планет и плазма радиационных поясов, плазма грозовых разрядов и газоразрядная плазма лабораторных устройств, “термоядерная” плазма современных термоядерных установок - вот далеко не полный перечень приложений науки о плазме. Наконец, в самые первые мгновения жизни Вселенной после Большого Взрыва, когда родился наш мир, как полагают, вещество также находилось в состоянии горячей плазмы, отголоском которого является реликтовое излучение, состоящее сейчас из “холодных” (с температурой около 2.7 К), а тогда “горячих” квантов, находившихся в равновесии с плазмой чудовищной тем-

пературы − в сотни миллионов и миллиардов градусов.

13

ГЛАВА 1

ОСНОВНЫЕ ПОНЯТИЯ И СВОЙСТВА ПЛАЗМЫ

§1. Образование плазмы, ее основные свойства

Для того, чтобы обычный газ перевести в плазменное состояние, необходимо ионизировать заметную часть молекул или атомов. Процесс ионизации является пороговым. Для ионизации электрон в атоме должен приобрести энергию большую, чем его энергия связи. Передача энергии, достаточной для разрыва этой связи, возможна при соударении атома или молекулы с другой быстрой частицей − электроном, ионом, атомом или молекулой, при взаимодействии с фотоном, при воздействии достаточно сильного электрического поля. При движении быстрого атома в сильном магнитном поле B возможна лоренц-ионизация.

В системе координат, относительно которой атом неподвижен, на него, согласно преобразованиям Лоренца, действует электрическое поле E=(v/c)B. Для ионизации атомов в электрическом поле пороговое значение поля составляет E~108 В/см, а ионизация из возбужденных состояний возможна при меньших полях E~106 В/см.

Если передаваемой атому энергии недостаточно для отрыва электрона, происходит возбуждение атома, которое снимается излучением кванта или передачей энергии другим электронам. В свою очередь, излученные кванты поглощаются другими атомами, либо свободно уходят.

Такую совокупность свободных заряженных и нейтральных частиц и квантов электромагнитного излучения американский физик Ленгмюр в 1928 г. назвал плазмой. Таким образом, плазма − это газ, но газ специфический: в нем могут присутствовать заряженные частицы сильно различающиеся по массе. Например, полностью ионизированная водородная плазма в качестве положительной компоненты содержит ионы водорода, т. е. протоны, а отрицательно заряженной компонентой являются электроны. Как из-

вестно, массы этих частиц равны

mp = 1.67x10-24 г , me = 0.91x10-27 г ,

14

и для отношения этих масс приближенно имеем mp/me = 1840.

Квазинейтральность

Плазма в целом должна быть электрически нейтральна, количество разноименных зарядов в достаточно большой единице ее

объема равны. В противном случае возникнут электрические поля, тем большие, чем больше дисбаланс зарядов, а создание таких полей требует совершения работы по разделению зарядов. Очевидно, что при отсутствии внешних воздействий эта работа может производиться только за счет кинетической энергии самих заряженных частиц.

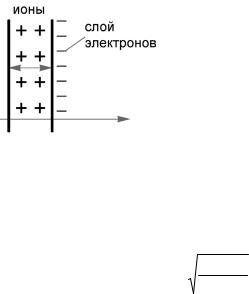
Предположим, что в некотором объеме флуктуативно разошлись заряды (рис.1.1) (считаем, что ионы покоятся, а электроны уходят) и оценим максимальное расстояние такого расхождения.

и она не может превышать кинетическую энергию теплового движения частицы, для одномерного движения, как известно, равную (1/2) kБТ, где kБ − постоянная Больцмана. Отсюда

На расстояниях, меньших d, всегда будут возникать электрические поля; флуктуации неизбежны. А вот разойтись на расстояния, существенно большие чем d, частицы не могут. Поэтому плазма и является квазинейтральной − нейтральная в больших объемах, но всегда с электрическими полями на расстояниях масштаба d, зави-

15

сящего от температуры и плотности плазмы. Величину d обычно называют дебаевским радиусом (см. ниже), употребительно также обозначение rD.

В физике плазмы температуру обычно измеряют в электронвольтах, при этом 1эВ эквивалентен 11600 K, и для ее обозначения в энергетических единицах вместо kБТ используют T. В книге в соответствии со сложившейся в русскоязычной литературе по плазме используется гауссова система единиц (см. Приложение I). Расчеты по (1.1) для термоядерной плазмы с параметрами n 1014см-3, Т 104эВ дают d 5 10-3см.

Плазменная частота

Электрические поля разделения зарядов будут действовать на заряженные частицы. Полагая, что существенно более тяжелые ионы покоятся, рассмотрим движение некоторого выделенного электрона в таком одномерном поле Е (см. рис. 1.1). Уравнение движения электрона

..

m x = −eE = −4πne2 x,

совпадает по виду с уравнением движения для одномерного осциллятора. Следовательно, электрон будет колебаться с частотой

Эту частоту, являющуюся одной из важнейших характеристик плазмы, называют плазменной или ленгмюровской. Следует подчеркнуть, что она не зависит от температуры. Для термоядерной плазмы с приведенными выше параметрами частота ленгмюровских колебаний оказывается равной ωp 6 1011c-1.

§ 2. Дебаевский радиус, дебаевский слой

Каждая заряженная частица в плазме взаимодействует с другими заряженными частицами, и распределение потенциала ϕ её поля зависит от пространственного распределения окружающих её частиц. В поле данной частицы плотность заряженных частиц в

16

равновесном состоянии плазмы должна быть распределена по закону Больцмана

где n0 – концентрация частиц невозмущенной полем плазмы, ϕ − потенциал электростатического поля. Напишем теперь уравнение Пуассона (в сферической системе координат) для частиц плазмы, окружающих выделенную частицу:

1 ∂∂ 2 (rϕ) = −4πe(Zni − ne ) . r r2

Учтем, что плотности электронов и ионов в поле выделенной частицы подчиняются закону Больцмана, а температуры Тe и Тi распределений электронов и ионов плазмы могут быть разными. Ограничиваясь линейным приближением, т.е. считая |eϕ|<<T, разложим экспоненты в ряд. Учитывая квазинейтральность плазмы (Znoi=noe), получим упрощенное выражение для уравнения Пуассона:

где q − заряд выделенной нами “пробной” частицы. Если это заряженный ион с кратностью ионизации Z, то q = Ze.

Вблизи частицы на расстояниях r<<rD потенциал поля совпадает с потенциалом поля частицы в вакууме (ϕ≈q/r), а на расстояниях r>> rD поле экспоненциально быстро затухает. На таких расстояниях от частицы плазма экранирует её электрическое поле. Поэтому уравнение (1.6) иногда называют уравнением экраниров-

17

ки. После того, как мы нашли характерное расстояние экранировки зарядов в плазме, можно дать более строгое ее определение: плаз-

ма – это квазинейтральный ансамбль заряженных (и нейтральных) частиц, размеры которого существенно больше радиуса Дебая.

Проникновение внешнего электростатического поля в плазму

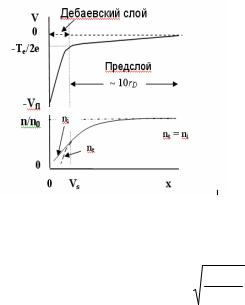
Поместим в плазму плоский электрод, имеющий потенциал ϕ по отношению к другому плоскому электроду, удаленному от данного на расстояние x>>d (рис.1.2). Примем для простоты Тe=Тi и Z=1, так что noi=noe=no. Тогда уравнение Пуассона для распределения потенциала вблизи электрода будет следующим:

(Предполагается, что ось х системы координат перпендикулярна к электроду)

Решение этого уравнения в предположении, что eϕ/T<<1, имеет следующий вид:

является радиус Дебая:

Вернемся к формуле (1.5). Если в ней положить, что ne=ni и Te=Ti, то получим выражение (1.8). Если считать, что плазма явля-

18

ется сильно неизотермической, так что Te>>Тi, то получим выражение, совпадающее с формулой (1.1) и отличающееся oт выраже-

ния, определяемого формулой (1.8), всего в 2 раз. Поэтому в любой плазме пространственные масштабы экранирования электрических полей и флуктуативного разделения зарядов практически одинаковы. Так же, как и ленгмюровские колебания с плазменной частотой, экранирование электрических полей − важная характерная особенность плазмы.

Отметим, что по порядку величины 1/ωp есть время пролета дебаевского слоя тепловым электроном.

Плавающий потенциал, т.е. потенциал, который приобретает внесенное в плазму изолированное тело за счет попадания на него более подвижных электронов, хорошо описывается формулой (в данном случае в связи с принятой практикой потенциал обозначен как V≡ϕ):

Это выражение получается из очевидного условия, что в стационарном случае ток положительных ионов скомпенсирован током электронов. Плотность потока электронов на поверхность определяется в соответствии с (1.3) уменьшенной отрицательным потенциалом тела концентрацией электронов с максвелловским распределением по скоростям:

где ve = 8Te , а Vs − потенциал на границе предслоя. Плотность

πme

тока ионов может быть найдена из критерия Бома, согласно которому для образования пристеночного слоя их скорость на границе при Te>>Ti должна определяться условием:

19

В общем случае обобщенный критерий Бома соответствует условию

где γ=1 для изотермического потока, γ = 5.3 для адиабатического потока с изотропным давлением и γ = 3 для одномерного адиабатического потока. Приравнивая плотности ионного тока ji = (nisvi ) / 4 , где vi определяется по (1.12) при γ =1, и электронно-

го тока (1.7) и, учитывая, что eVs ≈Te/2, получаем (1.9). Изменение этого потенциала с расстоянием качественно показано на рис.1.2.

Критерий (1.11) может быть получен из следующих соображений. Полагая, что образовавшиеся в области плазмы с потенциалом V=0 ионы имеют нулевую скорость (Ti=0), и достигли без столкновений границы предслоя со значением потенциала Vs , имеем:

Из условия непрерывности потока nv в пристеночном слое вытекает, что ni/nis=(Vs/V)1/2. Подставляя в уравнение Пуассона для слоя (1.7) и полагая плазму на границе слоя квазинейтальной (nis=nes=ns), имеем

Вводя переменную =Vs-V>0 и считая ее малой по сравнению с Vs и Te/e, путем разложения по V вблизи Vs правой части получаем:

Решение этого уравнения имеет неоциллирующий характер лишь при положительном значении множителя в скобках, откуда e/Te>1/2Vs, что в соот-

ветствии с (1.13) дает Mi vs2 /2>Te или vs ≥ (Te/Mi)1/2.

20