
Жданов Основы физических процессов 2007
.pdf
ведение заряженной частицы (назовем ее пробной), пролетающей через облако покоящихся заряженных частиц (назовем их полевыми). В идеальной плазме каждое взаимодействие двух частиц можно рассматривать независимо от наличия остальных, но при вычислении полного сечения взаимодействия надо учесть экранирование плазмой поля данной частицы.
Если пробная частица движется так, что при отсутствии взаи-
модействия |
она пролетела |
|
|
|
|
|
|
|
бы мимо |
полевой на |
|
|
|
|
|
|
|
расстоянии |
прицельного |
|
|
|
|
|
|
|
параметра ρ (рис. 1.7), то она |
|
|
|
|
|
|
||
отклонится на угол θ, зави- |
|
|
|
|
|
|
||
сящий |
от |
приведенной |
|
|
|
|
|
|
массы частиц μ, их зарядов Z |
|
|
|
|
|
|
||
и относительной скорости v: |
|
|
Рис.1.7. Схема упругого рассеяния |
|||||
где |
|
tgθ/2 = ρ /ρ, |
(1.27) |
|||||
|
|
|
|
|
|
|
|
|
|
|
ρ = |
Z |
1 |
Z |
2 |
e2 |
(1.28) |
|
|
|
μv 2 |
|||||
|
|
|
|
|
||||
прицельный параметр, при котором пробная частица отклоняется на угол π/2. По существу, такое рассмотрение соответствует описанию движения одной частицы с приведенной массой μ в поле центральных сил. Соотношение (1.27) позволяет найти зависимость дифференциального сечения рассеяния от угла и энергии частиц:
dσ 2πρdρ |
|
ρdρ |
|
|
ρ |
2 |
|
|
|
Z12Z22 |
|
|||||
|
= |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
, (1.29) |
|
|
|
|
2 |
|
|
2 |
|
4 |
|
||||||
dΩ |
dΩ |
sinθdθ |
= |
2sin |
(θ / 2) |
|
E |
sin |
(θ / 2) |
|||||||
|
|
|
|
|
|
|
|
|
||||||||
что представляет собой известную формулу Резерфорда. Скорость пробной частицы при упругом рассеянии меняется только по направлению, уменьшаясь в проекции на первоначальное направление на величину δv = v(1-cosθ). Этой величиной, проинтегрированной по углам рассеяния, определяется значение коэффициента диффузии. Другие коэффициенты переноса (вязкость, теплопро-
31

водность) связаны со среднеквадратичным приращением поперечной скорости частиц при упругом рассеянии v = v sin2θ= v(1- cos2θ). Проинтегрированные по углам сечения этих процессов отличаются примерно в два раза. Проведя интегрирование δv по всем углам рассеяния θ (или по всем значениям прицельного параметра ρ), умножив на число полевых частиц в единице объема n и на путь пробной частицы dx, можно получить величину изменения скорости частицы в первоначальном направлении:
|
2 |
∞ |
ρdρ |
||
dv = −4πnvdxρ |
|
∫ |
|
|
. |
|
ρ2 |
+ ρ2 |
|||
|
|
0 |
|
|
|
Очевидно, что этот интеграл логарифмически расходится на верхнем пределе. Однако следует учесть, что реально выделенная полевая частица экранируется окружающей плазмой и ее поле быстро уменьшается с увеличением расстояния. Характерное расстояние экранирования − дебаевский радиус d, и интегрировать следует в пределах 0 < ρ < d. Тогда получим
dv = −2πnvρ 2dx ln[1+(d/ρ )2].
Так как d/ρ >>1, то можно положить ln[1+(d/ρ )2]≈2Λ, где
|
d |
|
|
|
|
|
(1.30) |
||
|
||||
Λ = ln |
|
|
||
|
ρ |
|
||
кулоновский логарифм; величина Λ определяется рассеянием на малые углы, и обычно Λ≈ 10÷20 при изменении параметров плазмы в широких пределах.
Можно ввести (несколько условно) длину свободного пробега λ, определив ее как расстояние, на котором dv = −v, (т.е. скорость в первоначальном направлении обращается в ноль):
dv |
= − |
dx |
; |
(1.31) |
|
v |
λ |
||||
|
|
|
тогда, положив λ = nσ1 c , где σc сечение кулоновского рассеяния,
имеем
σc = 4πρ 2Λ. |
(1.32) |
32
Обратная пропорциональность длины свободного пробега концентрации и сечению рассеяния для твердых сфер с сечением σ = πа2 очевидна из следующих рассуждений. Если частица движется со скоростью v в среде с концентрацией n, то она испытывает nσv столкновений в единицу времени. Так как время между столкновениями τ =1/nσv, то длина пробега между ними λ=vτ = 1/ nσ.
При кулоновских соударениях σc сильно зависит от энергии
частиц (ρ = |
e2 |
|
) обратно пропорционально квадрату ее энергии |
|
μv |
2 |
|||
|
|
(или квадрату температуры):
σc ≈ E12 .
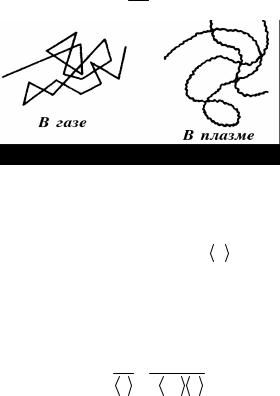
Рис.1.8. Траектория частицы в газе и в полностью ионизованной плазме
Для качественных оценок энергию относительного движения можно заменить на среднюю тепловую энергию E ≈T (с усреднением
по максвелловскому распределению по скоростям. В этом случае можно ввести зависящие от температуры эффективные сечения рассеяния, соответствующие им средние длины пробега и времена рассеяния. Тогда для времени рассеяния или кулоновского времени,
имеем:
τc = |
λ |
= |
1 |
v |
. |
(1.33) |
|
v |
|
n σc |
|
|
Легко видеть, что время рассеяния быстро растет с температурой
33
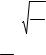
τc T3/2. |
(1.34) |
Т.е. по мере роста температуры заряженные частицы рассеиваются медленнее.
Траектория заряженной частицы в плазме существенно отличается от траектории нейтральной частицы в газе (рис.1.8): в плазме − это медленно меняющаяся плавная кривая.
§6. Неупругие процессы
Неупругих процессов огромное множество [1], но мы остановимся только на наиболее важных для физики горячей плазмы и рассмотрим их в соответствии с приведенной в §4 таб. 1.1. Причем сначала рассмотрим прямые процессы, затем обратные и отдельно остановимся на излучательных процессах.
Возбуждение, ионизация, диссоциация
Причиной возбуждения электронной системы атома может быть как поглощение кванта электромагнитной энергии, так и соударения частиц. Возбужденные состояния возможны для всех сложных частиц − молекул, атомов, молекулярных и атомарных ионов (кроме иона атома водорода). В молекулах и молекулярных ионах могут быть возбуждены вращательные, колебательные и электронные состояния, а в атомах и атомарных ионах − только электронные. С энергетической точки зрения, наиболее легко возбуждаются вращательные уровни, труднее колебательные, еще труднее электронные. Если принять за единицу расстояние между электронными уровнями δЕэ, то расстояние между колебательными
уровнями δЕν |
будет меньше в m раз, а между вращательными |
|
M |
уровнями δЕj еще меньше: в m раз, где M − масса молекулы, а m −
M
масса электрона. Например, для молекулы Н2 расчетные значения энергий возбуждения соответствующих состояний Еэ= 4,7 эВ, Еν= 0,54 эВ, Еj= 7,6 10-3 эВ. Колебательные возбуждения отмечают индексом ν, например АВν, вращательные − индексом j (или r), например DСj (или DСr).
34
|
|
Схематично возбуждение |
|||
|
|
при соударении с электро- |
|||
|
|
ном |
симметричной |
двух- |
|
|
|
атомной молекулы (Н2, N2, |
|||
|
|
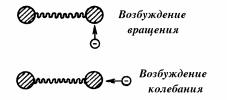
O2 и т.д.) показано на рис.1.9. |
|||
|
|
В таких молекулах дополни- |
|||
|
|
тельно к трем поступатель- |
|||
Рис.1.9. |
Схема возбуждения двух- |
ным степеням свободы могут |
|||
атомной |
молекулы электронным |
возбуждаться |
электронные, |
||
ударом |
|
две |
колебательные и |
две |
|
|
|
вращательные |
степени |
сво- |
|
боды. Очевидно, что в более сложных молекулах (например, CO2) могут возбуждаться несколько разных колебательных мод.
Существование вращательных и колебательных степеней свободы в молекулярных газах определяет основные свойства слабоионизованной плазмы этих газов и дает возможность использовать их в плазмохимических и лазерных системах. Дело в том, что сечения упругого и неупругого (с возбуждением колебательных степеней свободы) процессов почти одинаковы (отличаются в несколько раз), а передаваемая от электрона энергия отличается в сотни и тысячи раз: при упругом соударении молекуле передается малая (~m/М) доля энергии электрона (см. выражение (1.24)), а при возбуждении колебания передается энергия, соответствующая энергии перехода, т. е. масштаба десятых долей электрон-вольта. Колебательная релаксация (переход колебательной энергии в тепловую) весьма затруднена (при комнатной температуре − вероятность масштаба 10-5-10-9), и поэтому реализуется существование систем с высокой колебательной температурой при малой поступательной (тепловой). Так можно обеспечить высокую инверсную заселенность колебательно-вращательных переходов, т.е. создать активную среду для лазеров.
Для слабоионизованной низкотемпературной плазмы характерно большое число колебательно-вращательно возбужденных молекул по сравнению с числом электронно-возбужденных. Заселение колебательно-вращательных уровней происходит активно при некоторых химических реакциях (например, горение углерода в кислороде с образованием СО − до 90% энергии ассоциации СО идет на возбуждение), в тлеющем разряде. Тушить возбуждение
35
можно различными путями — излучением (используется в лазерах), частичным переходом энергии возбуждения в энергию химических связей (используется в плазмохимии). По мере повышения температуры газа увеличивается число частиц с электронным возбуждением.
В обычных условиях электрон находится в атоме, молекуле (или ионе) в основном состоянии, соответствующем минимуму его потенциальной энергии. Получив некоторую добавочную энергию (от фотона или другой частицы), электрон может перейти на более высоколежащий энергетический уровень. Это − электронновозбужденное состояние. Вероятность такого процесса определяется соответствующими сечениями возбуждения и сильно зависит от способа возбуждения. Возбуждение при соударении с частицами определяется величиной относительной скорости, зарядовым состоянием cоударяющихся частиц и имеет резонансный характер. При этом, согласно критерию Месси (выражение (1.21)), адиабатически маловероятными будут такие процессы, при которых при небольшой относительной скорости частиц для возбуждения того или иного уровня необходима существенная энергия. Так, практически не возбуждаются колебательные уровни энергии при тепловых скоростях молекул.
Сечение неупругого перехода атома из состояния 0 в состояние n согласно квантовой механике определяется амплитудой (матричным элементом)
соответствующего перехода fon и отношением волновых чисел q = p / h
dσ |
= |
qn |
|
|
f0n |
|
2 . |
|
|
|
|
||||||
dΩ |
q0 |
|||||||
|
|
|
|
|
||||
При возбуждении электронами, энергия которых существенно превышает энергию перехода, применимо борновское приближение, для которого
|
me |
∫ |
* |
r′ |
−ikrrr |
r′ |
r′ |
r′ |
|
|
f0n = − |
|
Ψn |
(r )e |
U (r, r )Ψ0 |
(r )drdr |
. |
||||
2πh2 |
||||||||||
|
|
|
|
|
|
|
|
|||
Здесь Ψ − волновая функция атома, r′− совокупность координат электрона, |
|||||
kr = qnnr − q0 |
− |
величина |
предаваемого |
электрону |
импульса, |
U − потенциальная энергия взаимодействия налетающего электрона с атомными электронами и ядром атома с зарядом Z
U = ∑ rr |
e2 |
Ze2 |
|||
− rr − |
r |
||||
|
|
|
|
|
. |
i |
i |
|
|
|
|
36
Полное сечение возбуждения пропорционально квадрату оператора дипольного момента атома D = ∑erri и некой универсальной
i
функции от отношения энергии электрона E и разницы уровней энергии E0n, между которыми происходит переход ϕ(E/ E0n). Для описания излучения диполя вводят безразмерную величину – силу осциллятора
F0n = (2me |
E0n/ h 2e2) D |
2 . |
|
0n |
|
С ее использованием сечение возбуждения (или неупругого рас-
сеяния электрона) представляется в виде |
|
|
|
|
|
||||
|
2πne |
4 |
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
σ0n = |
|
|
F0nϕ |
|
. |
|
|
|
(1.35) |
( E |
)2 |
E |
|
|
|
||||
|
0n |
|
|
0n |
|
|
|
|
|
|
|
|
|
Графическое |
представление |
||||
|
|
|
|
функции ϕ(E/ |
E0n) показано |
||||
|
|
|
|
на рис.1.10. Эта функция |
|||||
|
|
|
|
имеет |
порог |
при |
х ≡ |
||
|
|
|
|
E/ E0n~2, затем достигает |
|||||
|
|
|
|
максимума в районе х ≈ 4, а |
|||||
|
|
|
|
при больших значениях ар- |
|||||
|
|
|
|
гумента |
ведет |
себя |
как |
||
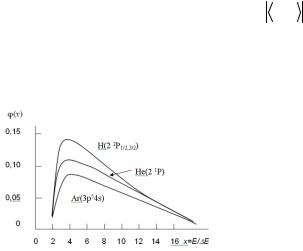
Рис.1.10. Вид функции ϕ(E/ E0n) |
в вы- |
(lnx)/x. |
|
|
|
|
|||
ражении для сечения |
возбуждения |
|
Качественно похожий |
||||||
(1.35), восстановленный |
из измерений |
вид зависимости сечения от |
|||||||
для различных переходов в аргоне, ге- |
энергии электрона и разно- |
||||||||
лии и водороде |
|
|
|
сти уровней можно полу- |
|||||
|
|
|
|
чить и в квазиклассическом |
|||||
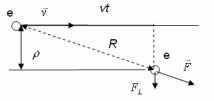
приближении, если положить, что быстрый электрон передает энергию внешнему (покоящемуся) электрону атома при их парном соударении (см. рис.1.11).
При этом предполагается, что налетающий со скоростью v электрон не отклоняется от своего первоначального направления и не тормозится Уравнение движения атомного электрона в направлении, перпендикулярном направлению движения налетающего электрона, в этом случае:
37
m |
dv |
= F = |
e2 |
|
|
ρ |
|
|
, |
|
[(vt)2 + ρ2 |
] |
[(vt)2 + |
ρ2 |
]1/ 2 |
||||
e dt |
|
|
|
||||||
где ρ − прицельный параметр. Энергия, приобретенная связанным электроном E = p2/2me.
Переданный импульс находится интегрированием F по
времени от -∞ до +∞. Откуда E = e4/Eρ. Выражая ρ через
E и |
E и подставляя в |
|
Рис.1.11. К модели Томсона |
|||||
дифференциальное |
|
сечение |
|
|
|
|||
|
|
|
||||||
рассеяния, имеем |
|
|
|
|
|
|
|
|
|
dσ = |
|
2πρdρ |
|
= |
|
πe4 |
d( E) . |
|
|
|
|
|||||
|
|
|
E( E)2 |
|||||
|
|
|
|
|
|
|
||
Интегрирование этого выражения по переданной энергии от 0 до энергии, соответствующей переходу E0n, дает окончательное выражение для сечения возбуждения в виде
|
πe |
4 |
|
1 |
|
1 |
|
|
σ0n = |
|
|
− |
|
(1.36) |
|||
E |
E |
|
||||||
|
E . |
|||||||
|
|
|
|
0n |
|
|
|
|
Таким образом, сечение так же как и в формуле (1.35), зависит от энергии электрона и разности уровней, имеет порог и максимум.
Величина сечения возбуждения электронных уровней лежит в диапазоне 10-16−10-18см2.
Для ионизации частицы необходимо сообщить хотя бы одному ее электрону энергию большую, чем энергия его связи с этой частицей. Энергия, необходимая для ионизации, выраженная в электрон-вольтах, численно равна разности потенциалов в вольтах, которую должен пройти электрон для ее приобретения. Поэтому часто говорят не об энергии ионизации, а о потенциале ионизации. Легче всего оторвать первый, как правило, внешний, электрон, второй и последующие − труднее. Наибольший первый потенциал ионизации у Не (24,5 В), наименьший у Cs (3,9 В). Второй потенциал обычно превышает первый в 2-3 раза, исклю-
38
чением являются щелочные металлы: наибольшая разница у Li (5,4 и 75,6 В соответственно).
Сечение ионизации при электронном ударе имеет качественно такой же вид, как и при возбуждении. Фактически, выше воспроизведено квазиклассическое рассмотрение процесса ионизации Томсоном. Подставив в формулу (1.36) вместо энергии возбуждения на некоторый уровень E0n энергию ионизации I, получаем формулу Томсона:
σ0n = |
πe4 |
|
1 |
− |
1 |
|
|
|
|
|
|
. |
(1.37) |
||
E |
I |
|
|||||
|
|
|
E |
|
|||
Порог ионизации совпадает с I, а максимум сечения приходится на энергию E=2I. Таким образом, для максимального значения
сечения ионизации из выражения (1.37) имеем σмах =πe4 / 4I 2 .
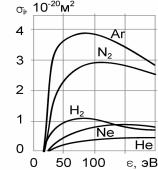
Рис.1.12. Сечения ионизация электронным ударом разных атомов и молекул
Для водорода энергия ионизации равна одному Ридбергу I ≡ Ry=e2/2aБ, откуда для максимального значения сечения ионизации имеем
σмах =πaБ2 . Если атом многоэлек-
тронный и имеет на внешней оболочке N (валентных) электронов, то сечение (1.37) надо умножить на N. На рис.1.12 приведены сечения ионизации для некоторых атомов. Как и для сечения возбуждения, сечение ионизации для разных атомов может быть представлено в виде единой аппроксимационной формулы
e |
|
Nπe4 |
f ( |
E |
|
|
|
σi |
= |
|
|
) , |
(1.38) |
||
I 2 |
I |
||||||
|
|
|
|
|
в которой f(E/I) с точностью ~20% имеет универсальный вид для различных ионов и молекул [1]. Следует иметь в виду, что экспериментально измеренные сечения ионизации достигают максимума при E/I~5.
39
Энергию ионизации можно передать и в процессе нескольких соударений, причем в каждом передается энергия меньше, чем необходимо для отрыва электрона. При каждом соударении частица получает энергию, переходит в более возбужденное состояние, а затем ионизуется уже из возбужденного состояния. Такая ступенчатая ионизация особенно важна в низко-температурной плазме, когда энергия электронов меньше потенциала ионизации. При этом сечение ионизации с возбужденного состояния существенно возрастает (более чем на порядок для He).
Образование иона возможно также при распаде так назы-
ваемого автоионизационного состояния нейтрального атома, в
котором энергетический уровень возбужденного связанного состояния атомной частицы и электрона находится выше границы непрерывного спектра, т. е. больше потенциала ионизации атома. Если возбуждено несколько электронов и если энергия возбуждения будет передана одному электрону, то произойдет ионизация – электрон перейдет в свободное состояние, а ион останется в основном (невозбужденном) состоянии. Следует отметить, что время жизни частицы в автоионизационном состоянии значительно больше характерного атомного.
Характер зависимости от энергии сечения ионизации ионным ударом качественно похож на таковой для электронного удара. И действительно, если, например, в модели Томсона налетающий электрон заменить протоном, то ход рассуждения не должен измениться, так как переданный импульс зависит только от относительной скорости частиц. Поэтому сечение ионизации ионным
ударом σii на шкале энергий должно быть сдвинуто в ~ Mi/me раз
(см. рис.1.14, на котором приведена сводка сечений основных элементарных процессов, важных для горячей водородной плазмы).
Ионизация возможна также при столкновении нейтральных атомов, один из которых возбужден (обозначается А*). Например, когда энергия возбуждения одного из атомов превышает энергию ионизации второго или образовавшейся при соударении молекулы. Процессы могут протекать по следующим основным схемам:
40
