Жданов Основы физических процессов 2007

и существенные отличия от световой, они в основном состоят в следующем:

1.Отдельные лучи в световой оптике независимы, а электронные лучи взаимодействуют друг с другом.

2.Показатель преломления для электронов всегда непрерывен, для света же он, как правило, меняется скачком.

3.Диапазон изменения показателя преломления для электронов не ограничен, в оптике n ≤ 4.

4.Скорость электронов тем больше, чем больше показатель преломления, а скорость света в среде, наоборот, падает с ростом n.

5.Преломляющие поверхности для электронов, в отличие от световых лучей, не могут быть произвольными – распределение потенциалов всегда удовлетворяет уравнению Лапласа (линейная электронная оптика) или Пуассона (нелинейная электронная оптика).

§39. Электростатические линзы

Для фокусировки заряженных частиц чаще всего используют диафрагмы (плоские электроды с круглым отверстием) с аксиаль- но-симметричным распределением потенциала U(z,r), который не зависит от азимутального угла θ. В разложении U по степеням r будут только четные степени:

U(z,r) = b0(z) + b2(z)r2 + b4(z)r4 + … + b2k(z)r2k + … (5.2)

Подставляя это выражение в уравнение Лапласа (в промежутке между электродами нет зарядов) в цилиндрической системе координат:

можно найти коэффициенты разложения, получив в итоге распределение потенциала в виде:

211

которое полностью определяется распределением потенциала на оси системы U(z) = U(0,z). Это сильно упрощает расчет движения электронов. Для приосевых электронов, движущихся примерно па-

раллельно оси (r/Lхар<< 1, ∂r / ∂z 1, где Lхар – характерный поперечный размер системы), которые еще называют параксиальными,

можно получить уравнение траектории. Для этого в распределении потенциала пренебрегаем слагаемыми со степенями выше r2, тогда уравнения движения электрона приобретает вид:

Первое уравнение системы замечательно тем, что в полях с аксиальной симметрией радиальная фокусирующая или расфокусирующая сила пропорциональна удалению частицы от оси. Однако следует иметь в виду, что это приближение и наличие в разложении фокусирующей силы слагаемых со степенями больше единицы приводит к искажениям изображения – аберрациям. Учитывая, что левые части уравнения содержат производные по времени, а правые производные по z, можно использовать переход к производной

уравнение с учетом граничного условия при z = 0 U(0) = 0 и dz/dt 0 = 0 (пренебрегаем начальной скоростью электронов, эмитируемых с катода с тепловой энергией, много меньшей приобретаемой энер-

гии в ускоряющем потенциале), получим dz/dt = 2eU (z) / m . Используя это соотношение для интегрирования второго уравнения и

212

которое называется основным уравнением электронной оптики.

Полученное линейное однородное дифференциальное уравнение 2- го порядка относительно U(z) и r(z) показывает, что возможно масштабное моделирование, т. е. если потенциал во всех точках пространства увеличить в k раз (увеличить потенциал на всех электродах системы в одинаковое число раз), то уравнение, а следовательно, и траектория электрона не изменится. Кроме того, уравнение не содержит отношения e/m, поэтому траектории электронов и ионов не отличаются.

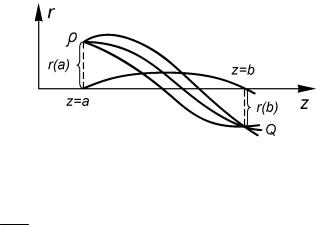
Если предметная плоскость находится при z = a, а плоскость изображения при z = b (рис. 5.3), то линейное увеличение линзы

Рис. 5.3. Изображение точки в линзе

M = rr((ba)) , где r(a) и r(b) расстояние до траектории от оси систе-

мы. Угловое увеличение линзы, определяемое как отношение тан-

213

главными плоскостями много меньше фокусных расстояний (b - a) << f1, f2 , т. е. главные плоскости сливаются, фокусные расстояния слева и справа определяются соответственно соотношениями:

тельное), т. е. линза всегда собирающая. Физическая причина фокусирующего эффекта такой линзы состоит в том, что и расстояние от оси (а значит и фокусирующая сила) и время движения электрона на фокусирующих участках всегда больше, чем на расфокусирующих.

Для одиночной диафрагмы с круглым отверстием:

где E1 и E2 – значения проекций напряженности электрического поля на ось системы слева и справа от диафрагмы, Ud – потенциал диафрагмы.

Для системы из двух линз – диафрагм с фокусами f1 и f2 и расстоянием между линзами l оптическая сила задается соотношением:

215

В общем случае аксиально-симметричного поля траектория электрона описывается уравнениями системы (5.5), т.е. фокусирующая сила определяется знаком второй производной от потенциала на оси системы. Если U′′(z) > 0, то система фокусирующая, если U′′(z) < 0, то расфокусирующая.

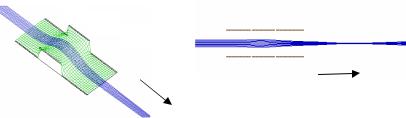
В общем случае для расчета непараксиальных пучков в электростатических системах эффективно используют пакеты прикладных программ. Наиболее известен пакет SIMION. В настоящее время доступны уже версии SIMION-7.0 и SIMION-8.0, которые позволяют рассчитать распределение полейA иB траекторииC заряженных частиц в них для аксиально-симметричных систем. На рис.5.6 в качестве примера приведено распределение потенциальной энергии и траектории ионов в системе из 2-х цилиндрических линз (линза Эйнцеля), на центральный цилиндрический электрод (B) подан положительный потенциал, а электроды A и C заземлены.

A

B

C

§40. Магнитные линзы

Фокусировку пучков в аксиально-симметричном магнитном поле проще всего продемонстрировать на примере параксиального пучка электронов, скорость которых вдоль оси системы много больше скорости в радиальном направлении vz >> vr. На электрон в

216

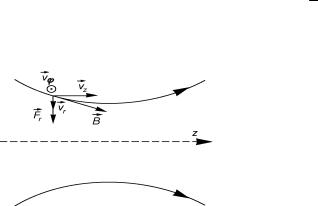
магнитном поле действует сила Лоренца Fr = − ce vr × Br . Радиаль-

ная составляющая этой силы является фокусирующей: Fr = -

(e/c)vϕBz (рис. 5.7).

Азимутальная составляющая скорости электрона появляется за счет азимутальной составляющей силы Лоренца:

Fϕ = -(e/c)(vzBr + vrBz) ≈ - (e/c)vzBr ,

так как vz >> vr. Составляющая скорости vz не меняет знака, радиальная составляющая магнитного поля Br меняет знак, при этом азимутальная составляющая скорости электрона vϕ будет уменьшаться

(вращение замедляться), но направление вращение никогда не меняется, поэтому фокусирующая составляющая силы Лоренца Fr всегда сохраняет знак. Таким образом, магнитная линза всегда собирающая.

С учетом теоремы Гаусса, дающей соотношения между продольной Bz и радиальной компонентами Br аксиальносимметричного магнитного поля Br = -(r/2)(dBz/dz), движение электронов вдоль оси описывается уравнением:

Азимутальное движение (поворот) описывается уравнением:

(ларморовское вращение), т. е. угловая скорость всех электронов (не зависимо от расстояния от оси) одинакова и изображение вращается как целое, причем, направление вращения зависит от направления магнитного поля. Если магнитное поле удовлетворяет

217

условию: ∫b Bz (z)dz = 0, то вращение изображения будет отсутст-

a

вовать. Учитывая, что для параксиальных пучков vz>>vr (в прибли-

жении mv2 2 ≈ U0 ), движение по радиусу задается уравнением:

где U0 – энергия электронов. Данное уравнение описывает траекторию в плоскости, которая вращается с ларморовской частотой. Как видно из уравнений движения, траектория электрона полностью определяется значением магнитного поля на оси Bz. В уравнения входят заряд и масса, следовательно, разные частицы движутся по разным траекториям. Уравнения линейны и однородны относительно расстояния от оси r, следовательно, любое аксиальносимметричное поле способно создать изображение и является линзой.

Для тонкой магнитной линзы (магнитное поле на оси быстро падает по мере удаления от линзы) оптическая сила:

или

218

Савара). Интегрируя (5.16), можно найти фокусное расстояние для одного токового витка:

Угол поворота:

§41. Отклоняющие и фокусирующие электронно-оптические системы

Отклонение и фокусировка заряженных частиц в электрическом и магнитном полях широко используется в устройствах и приборах для создания и диагностики плазмы, а также для исследования процессов взаимодействия плазмы с твердым телом. Рассмотрим некоторые из таких систем.

Электростатические энергоанализаторы

Электростатические энергоанализаторы чрезвычайно распространены в плазменных исследованиях ввиду их компактности, простоты конструкции и питания. Анализаторы могут быть с за-

219

держивающим полем (интегральные) и дисперсионные. В первом случае энергетический спектр анализируемых частиц находится путем дифференцирования зависимости приходящего на установленный за сеточными электродами коллектор (многосеточный зонд), во втором путем воздействия электрическим полем на траек торию. Рассмотрим три простых дисперсионных анализатора. Наиболее простой является система в виде плоского конденсатора.

Рис. 5.8. Фокусировка в электростатическом поле плоского конденсатора

Если пучок частиц запускается параллельно пластинам (рис. 5.8), то угол отклонения пучка α зависит от энергии частиц U0:

где Uоткл − разность потенциалов, приложенная к плоским электродам, l − длина пластин вдоль движения пучка, d − расстояние между пластинами. Благодаря различным значениям потенциала на верхней и нижней границе пучка, а значит и различным скоростям частиц, происходит фокусировка пучка. Поэтому, такие системы используются в электронно-лучевых экранах. Можно оценить фокусное расстояние (расстояние от центра системы до точки фокусировки) найдя значение Δα:

220