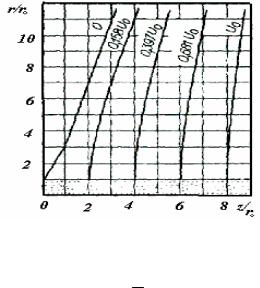
ускоряющего напряжения и разброса энергий электронов, излучаемых накаленным катодом. В магнитном электронном микроскопе колебание силы тока в обмотке линз приводит к дополнительному размытию изображения. Кроме просвечивающих электронных микроскопов широкое распространение получили сканирующие электронные мокроскопы, в которых изображение формируется отраженными от исследуемого образца или вторичными электронами.
ГЛАВА 6
ВЛИЯНИЕ ПРОСТРАНСТВЕННОГО ЗАРЯДА ЭЛЕКТРОННЫХ И ИОННЫХ ПУЧКОВ
§42. Ограничение тока пространственным зарядом в диоде
В промежутке длиной d между плоскими катодом и анодом рас-
|
пределение потенциала в вакууме линейно: U(x)=U(a) |
x |
(это рас- |
|
d |
|
|
|
|
пределение является решением уравнения Лапласа U = 0). По ме- |
ре увеличения плотности тока объемный заряд ρ(x) в промежутке
|
|
|
|
|
|
|
|
|
|
|
|
растет, изменяя распределение потенциала и приводя к |
|
|
|
|
|
|
возникновению |
вблизи |
поверх- |
|
|
|
|
|
|
|
|
ности |
катода потенциального |
|
|
|
|
барьера - «виртуального като- |
|
|
|
|
да», от которого электроны от- |
|
|
|
|
ражаются обратно на катод (рис. |
|
|
|
|
6.1). Для определения распреде- |
|
|
|
|
ления потенциала в промежутке |
|
|
|
|
необходимо |
решать |
уравнение |
|
|
|
|
Пуассона |
U= -4πρ(x) с учетом |
|
|
|
|
того, что плотность тока в про- |
|
|
|
|
межутке j = - ρv. Если считать, |
|
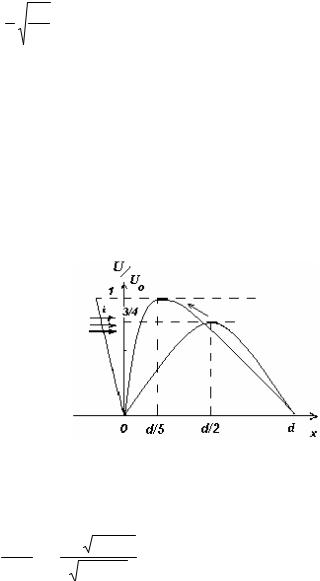
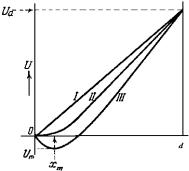
Рис. 6.1. Распределение потенциала |
|
что |
электроны |
эмитируются с |
|
в плоском диоде без влияния про- |
катода с нулевой скоростью (те- |
|
странственного заряда (I), в режиме |
пловая |
энергия |
эмиссионных |
|
ограничения тока объемным заря- |
электронов много меньше энер- |
|
дом (II) и в режиме возникновения |
|
виртуального катода (III) |
гии, |
приобретаемой |
в |
проме- |
|
жутке), то устойчивым |
|
|
|
|
|
|
является режим, когда «виртуальный катод» не образуется, а элек-
|
трическое |
поле на поверхности катода равно нулю: |
|
E = |
dU |
|
|
x=0 |
= 0 . При таком граничном условии в режиме ограни- |
|
|
|
|
dx |
|
|
|
|
чения тока объемным зарядом решением уравнения Пуассона
|
d 2U |
= |
4πj |
1 |
(6.1) |
|
dx 2 |
2e / m |
U |
|
|
|
(здесь учтено, что при начальной нулевой скорости энергия электронов mv2/2 = eU) является распределение потенциала в промежутке в виде:
U (x) =U (d )( |
x |
)4 / 3 . |
(6.2) |
|
|
d |
|
В этом случае плотность электронного тока, который можно пропустить через промежуток, ограничена величиной, зависящей от напряжения на аноде Ua и от расстояния между катодом и анодом d:
j3 / 2 [ А/ см |
2 |
] = |
2 e U a3 / 2 |
= 2.33 10 |
−6 |
U a3 / 2 [В] |
. (6.3) |
|
9π me |
d 2 |
|
d 2 |
[см] |
|
|
|
|
|
|
Это соотношение получило название закона Чайльда-Ленгмюра, или закона «3/2». Для ионного тока:
ji [ А/ см] = |
2 e |
U 3 / 2 |
= 5.46 |
U 3 / 2 |
[В] |
. (6.4) |
9π M i |
a |
a |
|
|
d 2 |
|
M i [а.е.м.]d 2 |
[см] |
Если учитывать начальную скорость эмитированных электронов v0, то уравнение Пуассона примет вид:
|
d 2U |
= |
4πj |
, |
(6.5) |
|
dx 2 |
v0 1 + 2eU /(mv02 ) |
|
|
|
|
|
решением которого является зависимость |
|
|
|
U(x) = (mv02/2e)((x/xm-1)4/3-1). |
(6.6) |
Около катода возникает «виртуальный катод» (потенциальный
|
|
mv2 |
на расстоянии xm = |
mv3 |
|
|
барьер) глубиной eUm= |
0 |
0 |
от катода |
|
2 |
18πej |
|
|
|
|
(рис.6.1).
Для цилиндрических диодов предельная плотность электронного тока зависит от напряжения на аноде в степени 3/2, но зависимость от расстояния между катодом и анодом носит более сложный характер (как результат решения уравнения Пуассона в цилиндрических координатах) и описывается специальной функцией Бо-
гуславского β( ra ) , где ra и rk – радиусы анода и катода соответст- rk
венно:
j3/ 2 = |
1 |
|
2e |
|
|
Ua3/ 2 |
|
. |
9π |
m |
|
r |
2 |
β |
2 |
( |
ra |
) |
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
rk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для приходящего на анод полного тока I3/2=j3/2Sa щадь анода.):
I |
|
[ А] = |
1 2e |
|
U 3/ 2 S |
a |
|
= 2.33 10−6 |
U 3/ 2[В]S |
[см2 ] |
|
|
|
|
|
|
|
|
a |
|
|
|
|
a |
|
a |
|
|
|
|
(6.8) |
3/ 2 |
9π m |
|
|
2 |
|
2 |
|
ra |
|
|
|
2 |
|
ra |
|
|
|
|
|
r |
β |
( |
) |
|
r |
2 |
[см]β |
( |
) |
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
rk |
|
|
a |
|
|
|
rk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− формула Ленгмюра-Богуславского. Значения функции Богуславского для широкого диапазона ra/rk можно найти в таблицах [29].
Распределение потенциала в промежутке описывается соотношением:
U (r) =U |
|
|
r |
)3 / 2 |
|
β 2 (r |
/ r |
) |
)2 / 3 . |
|
a |
( |
|
( |
|
k |
|
(6.9) |
r |
β 2 (r |
/ r |
) |
|
|
|
a |
|
|
a |
k |
|
|
Для сферического диода полный ток на анод Ia:
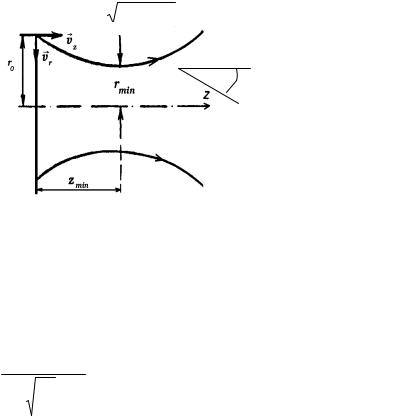
Рис. 6.2. Распределение потенциала в пролетном промежутке
I a [ А] = |
4 |
2e U a3 / 2 |
|
= 29.3 10 |
−6 U a3 / 2 |
[В] |
, |
(6.10) |
9 |
m |
e |
α |
2 |
( |
rk |
) |
|
α |
2 |
( |
rk |
) |
|
|
|
|
|
|
|
|
|
r |
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
a |
|
|
|
где α(ra/rk) – табулированная функция Ленгмюра [30]. Распределение потенциала между катодом и анодом в этом случае:
|
U (r) =U (a)( |
α(rk / r) |
)2 . |
(6.11) |
|
α(r |
/ r ) |
|
|
|
|
|
|
k |
a |
|
|
§43. Предельная плотность тока пучка частиц в пролетном промежутке в вакууме
Плотность тока заряженных частиц в пролетном промежутке между электродами с одинаковым потенциалом ограничена также из-за собственного объемного заряда и, соответственно, потенциала пучка.
Рассмотрим эту задачу
(задачу Бурсиана) на примере потока в пролетном промежутке длины d ионов массы M, ускоренных до этого в плоском диоде потенциалом U0 (рис. 6.2). Распределение потенциала в
промежутке задается уравнением Пуассона:
|
d 2U |
= − |
4πj M / 2e |
. |
(6.12) |
|
dx 2 |
U 0 −U |
|
|
|
|

Устойчивое решение этого уравнения при граничных условиях U(0) = U(d) = 0 существует только при дополнительном граничном условии на поле [31]:
|
|
Ε 0 = dψ/dξ 0 < 2 , |
(6.13) |
где |
ψ = U/U0, ξ = x/rd, r |
= Mv |
2 |
/(4πne 2 ) - дебаевский радиус |
|
d |
|
0 |
|
|
пучка. Это условие соответствует условию на максимальную длину пролетного промежутка:
d < (4 2 /3)rd = dmax. |
(6.14). |
Значение dmax соответствует критическому значению максимума потенциала:
При возрастании плотности ионного тока потенциал в пролетном промежутке будет возрастать до Umax, затем скачком возникает «виртуальный анод» с Umax = U0, от которого произойдет отражение части ионов (ионы имеют распределение по энергиям) обратно в сторону источника, в результате чего ток на коллектор уменьшится в 4.5 раза. Таким образом, ток в пролетном промежутке ограничен током Бурсиана:
jБ |
= |
8 |
2e U 03 / |
2 |
(6.16) |
9π |
M d 2 |
= 8 j3 / 2 . |
|
|
|
|
Механизм этой неустойчивости Бурсиана связан с положительной обратной связью между частицами пучка и внешней электрической цепью, когда повышение потенциала пучка на малую величину автоматически вызывает дальнейшее его повышение. Эта связь возникает, когда дебаевский радиус пучка становится меньше расстояния между электродами. Точно такое же ограничение существует и для потока электронов в вакууме. Даже в случае скомпенсированного пучка электронов, когда пространственный заряд элек-
тронов в пролетном промежутке скомпенсирован ионами (задача Пирса), возникает ограничение на максимально возможную плотность тока из-за неустойчивости, также приводящей к образованию виртуального катода и запиранию пучка. Физическая причина в данном случае пирсовской неустойчивости та же, что и неустойчивости Бурсиана, – положительная обратная связь электронов пучка с электронами внешней электрической цепи, которая возникает, если дебаевский радиус пучка становится меньше расстояния между электродами. Качественно эти неустойчивости сродни пучковой неустойчивости, при которой энергия направленного движения передается в энергию плазменных колебаний (см. §37). Условием устойчивости на длину пролетного промежутка в случае скомпенсированного потока является d < πrd, а предельная плотность тока (ток Пирса) равна:
jП |
= |
π |
2e |
U 3 / 2 |
≈ |
π |
2 |
(6.17) |
+ (m / M )1 / 3 ) |
0 |
9 |
j3 / 2 . |
|
4(1 |
m |
d 2 |
|
4 |
|
|
Расхождение пучков заряженных частиц под действием собственного объемного заряда
Основной проблемой транспортировки интенсивных пучков заряженных частиц является их расхождение под действием собственного объемного заряда. Для отыскания формы пучка необходимо решать уравнение Пуассона (для ленточного пучка двумерное):
∂2U |
+ |
∂2U |
= −4πρ(x, z) , (6.18) |
∂x2 |
|
∂z2 |
|
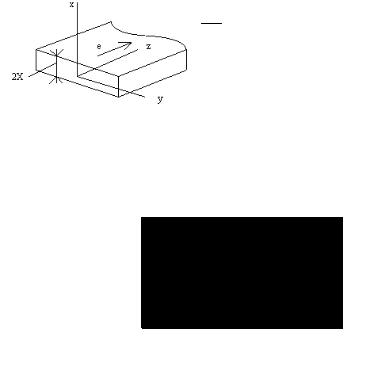
а также уравнение движения для граничной заряженной частицы. В случае бесконечного ленточного пучка (рис.6.3), у которого ширина значительно больше толщи-
Рис. 6.3. Плоский электронный ленточный пучок
ны 2X, для определения электрического поля на границе вместо уравнения Пуассона можно использовать теорему Гаусса о равенстве потока электрического поля через поверхность и заряда, заключенного в объеме, ограниченном этой поверхностью. Тогда напряженность электрического поля на границе:
|
|
Ex = J/(2ε0v)=J/(2ε0 2eU 0 / m ), |
(6.19) |
где |
ε0 |
= 8.85 10−12 Кл/(В м) |
|
– |
|
|
диэлектрическая |
γ |
постоянная вакуума, J – |
|
линейная плотность тока (ток |
|
на |
|
единицу |
ширины |
|
бесконечного |
|
ленточного |
|
пучка), |
U0 |
– |
потенциал, |
|
которым был ускорен пучок |
|
до |
входа |
в |
пролетный |
|
промежуток. |
|
Решая |
|
уравнение движения mx&&= eEx , получим профиль
границы пучка, которая описывается зависимостью x(z):
Рис. 6.4. Расходимость цилиндрического электронного пучка под действием собственного объемного заряда
x = x0 - tgγ z + pz2/2 , |
(6.20) |
где p = |
J |
, γ - угол сходимости пучка на входе, т. е. |
2e |
|
4ε0 |
U 03 / 2 |
|
|
|
|
m |
|
угол между направлением скорости граничного электрона и направлением распространения пучка по оси z. Местоположение самого узкого в поперечном размере участка пучка, так называемого «кроссовера» zкросс, определяется из условия:
dx/dz = 0, т.е. zкросс= tgγ/p. |
(6.21) |
Для цилиндрического пучка, влетающего в пролетный участок параллельно оси z с начальным радиусом r0, зависимость радиуса пучка r(z) задается соотношением:
z |
|
e |
U 3 / 4 |
R |
ς |
|
|
U 3 / 4 |
[кВ] R |
ς |
|
|
|
= 4 |
0 |
∫ |
d |
|
= 32.3 |
0 |
|
∫ |
d |
|
, |
(6.22) |
r |
2m |
I 1 / 2 |
ln |
ς |
I 1 / 2 [мА] |
ln |
ς |
0 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
где I – полный ток пучка, ускоренного потенциалом U0, R=r/r0 (числовой коэффициент дан для электронного пучка). Для сходящегося пучка, входящего в пролетный промежуток под углом γ к оси z
(рис. 6.4):
rz = |
2me U 0 ∫R |
8e |
dς |
. |
(6.23) |
0 |
1 |
I ln ς + 2e U 0 tg 2γ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mU 0 |
|
m |
|
|
Радиус пучка в наиболее узком месте (в кроссовере) определяется из соотношения:
ln |
r |
= |
U 3 / 2 |
e |
tg 2γ ≈1.04 103 |
U 3 / 2 |
[кВ] |
tg 2γ , (6.24) |
0 |
0 |
2m |
0 |
|
|
r |
|
I |
|
I[мА] |
|
|
min |
|
|
|
|
|
|
|
где численный коэффициент дан для электронного пучка. Для нахождения положения кроссовера нужно в (6.23) взять R = rmin / r0 .
При выводе этих соотношений не была учтена сила Лоренца, действующая на движущуюся заряженную частицу в магнитном поле. Эта фокусирующая сила в собственном магнитном поле тока пучка будет существенна только при достаточно больших скоростях частиц, так как отношение силы Лоренца к электрической силе расталкивания равно отношению квадратов скорости электронов и скорости света.
Расхождение пучков ограниченных поперечных размеров следует учитывать не только в пролетных промежутках, но и в электронных или ионных пушках. Пирсом было показано, что можно подобрать форму окаймляющих пучок промежуточных
электродов так, чтобы компенсировать расталкивающее действие объемного заряда пучка и сохранить прямолинейность его распространения (пушки Пирса). Для этого необходимо, чтобы для потенциала в пространстве вне пучка, удовлетворяющего в случае
плоской геометрии уравнению Лапласа: ∂2U + ∂2U = 0 , на грани-
∂x2 ∂z2
це пучка выполнялось условие ∂U/∂x = 0 (рис.6.3).
Рис. 6.5. Геометрия эквипотенциалей в пушке Пирса, формирующей параллельный пучок
Решение уравнение Лапласа с учетом этого условия и зависимости потенциала на оси U (z) =U (d )( dz )4 / 3 позволяет определить тре-
буемую геометрию электродов, которая для плоского случая задается уравнением:
(x2 + z2 )2 / 3 cos( |
4 arctg(x / z)) =U (d ) . |
(6.25) |
|
3 |
|
Угол наклона плоскости катода (U = 0) к направлению распространения пучка arctg(x/z) = 3π/8 = 67.5о. В случае цилиндрической геометрии численный расчет показывает, что угол наклона электрода, прилегающего к катоду, также составляет 67.5о (рис. 6.5).